多项分布内生回归元计数模型的两阶段估计方法研究

赵 娜，洪广彬

(1．南开大学 经济学院，天津 300071;2．塔夫茨大学 经济系，马萨诸塞州 梅德福02155)

一、引 言

在微观经济研究中，通常需要考虑计量经济模型的内生性问题。所谓内生性，是指模型由于遗漏变量、存在测量误差以及回归元和因变量间具有相互因果关系等，造成某些回归元与随机扰动项之间相关，从而导致模型参数估计有偏或者不一致［1］，如何解决内生性问题一直是学术界普遍关心的热点话题。传统的工具变量(Instrument Variable，IV)估计是学者们最早提出解决内生性问题的方法，已被广泛用于处理线性计量模型的内生性问题。然而，Martens等提出选择合理的工具变量是实际应用中面临的重要难题，这是由于IV估计在实际应用中会受到诸多限制［2］;Nelson等在讨论IV估计量的精确样本分布特征时，发现样本容量较小会导致参数的有偏估计［3］;Bound等研究指出，工具变量与内生回归元之间的弱相关性会引起模型参数估计的严重偏倚和非一致性［4］。

为更好地解决内生性问题，由传统IV估计方法衍生形成的两阶段估计方法逐渐被学者们广泛采用。两阶段最小二乘法(Two-Stage Least Squares，2SLS)主要应用于经典的线性计量经济模型中，不仅能够大大简化完整信息极大似然估计的计算复杂难题，而且估计结果具有良好性质［5］。随着计量经济学的发展和微观统计数据的完善，现代社会科学领域的经验性研究越来越多地开始使用非线性计量模型，如离散选择模型、计数模型和受限因变量模型等，然而相关研究发现，当内生回归元为服从某一特定分布的离散型变量时，忽略内生回归元的特殊性质而仍然采用2SLS法，就会导致非一致的参数估计量［1，5］。因此，适用于线性模型的2SLS方法不能直接推广到非线性模型中使用，而两阶段预测值替代(Two-Stage Predictor Substitution，2SPS)和两阶段残差引入(Two-Stage Residuals Inclusion，2SRI)方法则应运而生，并被 Shin［6］、Fabbri等［7］学者迅速应用于大量的实证研究中。

在健康经济学领域中，学者们常常采用计数模型探讨健康状况与医疗需求等问题。在这类研究中，大多是从有无保险、健康状况、职业状态等方面进行分析，而这些影响因素也往往表现为服从二项分布或多项分布的变量，并且具有内生性，例如 Deb［8］、Geraci等［9］探讨了医疗保险类型与医疗需求的关系。近些年来，国内学者也开始采用计数模型分析中国医疗保障与医疗服务需求的关系，但较少利用2SPS和2SRI处理内生性问题［10－11］。尽管 2SPS和 2SRI方法都会得到不一致的参数估计量，但是基于2SRI方法构造的内生性检验却具有良好性质［1］。Staub通过对比分析豪斯曼检验和基于2SRI法构造的沃尔德检验的有限样本表现，发现后者计算简洁且检验结果更稳健［12］。Geraci等通过包含离散内生解释变量的计数模型，比较了基于2SRI方法构造的Wald、LR和LM检验方法，结果验证了LM检验统计量在有限样本下的有效性［9］。

在现有文献的基础上，本文延续前人的研究工作［8－9］，在包含多项分布内生回归元计数模型的基础上，采用蒙特卡洛模拟实验，从模型形式的设定、计数数据分布特征和样本容量等方面，对三种两阶段估计方法(2SLS、2SPS、2SRI)进行系统的比较分析，并对Wald、LR、LM三种内生性检验方法的检验功效和过度拒绝特征进行综合评价。

二、模型和方法

(一)一般非线性模型的参数化表示与内生性

在探讨2SPS和2SRI方法的有限样本特征时，研究数据的生成过程主要有两种:传统方法是在简约型方程与行为方程中引入随机生成但彼此相关的误差项，并将这种相关性由简约型方程传递给内生变量，从而导致由简约型方程生成的变量在行为方程中与其误差项相关，最终造成行为方程具有内生性［5，12］;另一种方法是将随机生成的潜在因子同时引入简约型方程和行为方程中，使行为方程中的误差项与部分回归元相关而造成内生性［8－9］。与传统方法相比，后者的优势在于能够用潜在因子来表示个体不可观察异质性对于简约型方程与行为方程的影响，会具有更丰富的经济学含义和现实意义。因此，设定带有内生变量的非线性模型为:

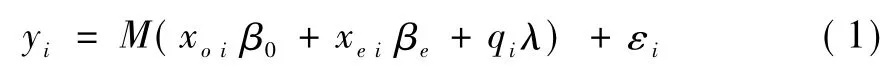
其中M(·)是已知某种形式的非线性方程;i为样本个体序号;xoi为一个1×K的可观测外生变量向量;xei为一个1×S的协变量向量，且与一系列S个不可观测的干扰变量qi相关，因此为内生变量向量，同时假定不可观测干扰变量qi的个数与内生协变量xei的个数相同［5，9］;β0、βe和 λ 是模型的参数向量;ε 为模型随机误差项，且E(εi|xoi;xei;qi)=0。模型(1)的条件均值方程为:

由于模型存在内生性问题的根本原因是协变量xei与不可观测干扰变量qi之间具有相关关系，因此为解决内生性问题，需要引入工具变量来处理内生性所导致的估计偏差。这里，构造S个包含内生协变量xei与不可观测干扰变量qi的简约型模型，即:

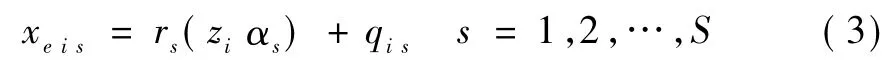
其中r(·)为已知某种形式的非线性函数;zi=［xoi，wi］，其中wi为一个1×S+的工具变量向量，如果wi为一个有效的工具变量向量，应该满足以下条件:wi与内生协变量xei高度相关、与外生变量xoi和随机误差项εi均不相关，并且工具变量之间互不相关，同时工具变量的个数不应小于内生协变量的个数，即S+≥S;αs是模型的回归系数;qis为模型的随机误差项。

在一般非线性模型的基础上，用服从多项分布的变量di代替模型(1)中的xei，并设定因变量yi对外生变量集xoi、多项分布变量集di和不可观测干扰变量集qi建立计数模型，其条件均值方程为:

由于计数变量的取值具有非负、离散和过度分散的特点，本文设定计数变量yi服从负二项分布，则条件概率密度函数可以表示为:

其中μi为yi的条件均值，即μi=E(yi|xi;di;qi) =exp(xiβ0+diβe+qiλ);φ 为过度分散系数，即 φ =1/α(α ＞ 0);yi的条件方差可表示为μi(1+φμi)。本文采用随机效应模型生成虚拟变量dij，表示个体i根据随机生成的效用值来选择选项j，以满足其自身预期效用最大化，而个体 i选择选项j的预期效用为EVij=αj+qij，如果选项j能够使个体i的预期效用达到最大，那么EVij≥ EVik(k≠ j)必然成立;虚拟变量dij表示个体i的选择结果，如果个体i选择了选项 j，dij=1，否则dij=0;同时，将选项0的效用进行标准化，即EVi0=0，并且用多项 Logit模型估计dij的取值概率分布，即设定dij的简约型方程为多项Logit形式:

(二)两阶段估计方法

在2SLS的估计过程中，首先以计数模型中的每个内生协变量dij为因变量、以工具变量zi为自变量，构造简约型模型dij=αj+qij，并进行最小二乘估计;然后利用估计模型得到预测值，并用替代行为方程中的di后，再进行最小二乘法估计。如果忽略不可观测干扰变量qi的存在，就相当于未考虑内生性问题，即是把qiλ项并入误差项 ε中，那么估计的实际误差项 εOLS应为 εOLS=qiλ + ε，而qi与di相关，会造成误差项与内生协变量di相关，出现内生性问题，最终会导致严重的估计偏差;但在2SLS的第二步估计中，采用代替di，使得被OLS忽视的不可观测干扰变量qi被合并到误差项中，此时的模型实际误差项ε2SLS为而被估计的模型为，这样误差项与di和xi均不相关，内生性问题得以解决。因此，当简约型方程和行为方程均满足线性条件时，2SLS可以很好地解决模型的内生性问题。

2SPS可以看作是2SLS在非线性模型中的拓展，这两种估计方法的步骤类似，但是2SPS法允许简约型方程与行为方程都可以选择更加符合现实的非线性模型，因而模型参数的估计方法也变成了非线性最小二乘法或者极大似然估计法。在第一阶段中，采用多项Logit模型估计简约型回归方程，得到预测值为然后，去掉计数模型中不可观测的干扰变量qi，同时用第一阶段的代替内生协变量di，并利用非线性最小二乘法或其他估计方法来估计行为方程yi=M(xoi如果 M(·) 是非线性函数形式，那么βe和qiλ都不能从非线性函数中分离出来，并会被合并到误差项中，所以内生协变量与误差项间的相关性并没有被完全消除。因此，2SPS方法实际上不能很好地解决非线性模型中的内生性问题。

2SRI方法的第一阶段估计过程与2SPS方法相似，同样需要用多项Logit模型估计简约型回归方程，并得到多项选择的预测结果 ^Pr(dij|zi);然后，计算估计模型的残差值，并将其引入计数模型结构型方程中，替换不可观测的干扰变量qij，得到:

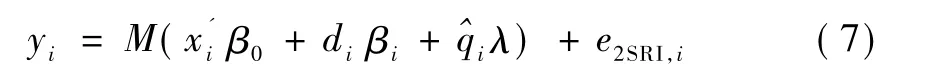
这里，残差e2SRI的计算方式有两种:第一种是由学者Cameron等提出的，并命名为原始残差(raw residuals)［13］:

第二种计算方式是由Pagan等于1989年提出的标准化残差(standardized residuals)，即对第一阶段估计的残差结果进行单位方差标准化，具体形式为［14］:

那么，模型(7)可以被重新表示为:由于模型(10)中不可观测的干扰变量被简约型回归方程所估计并引入计数模型中，因而遗漏变量问题得以解决，并且误差项和均不相关，所以计数模型的内生性被消除。然而，已有研究文献并没有对这两种残差形式的性质得出一致的理论分析结论，本文将在后续蒙特卡洛模拟实验中对二者的有限样本特征进行探讨。

(三)内生性检验方法

关于计量经济学模型的内生性检验，可以采用Wald、LR、LM三种检验统计量，三种检验方法都是基于极大似然估计，并在大样本下都具有渐近一致性，但这三种检验方法在针对带有多项分布内生回归元的计数模型时，其有限样本特征却未被详细讨论。因此，本文将基于这类计数模型对检验方法的有限样本性质进行探讨。一般地，原假设常常表述为模型中不存在内生性问题，亦即模型中不存在被忽略的不可观测干扰变量，因此计数模型内生性检验的原假设为 H0:λi=0(i=1，2，…，S);如果假设检验的结果表明原假设被拒绝，那么就说明原模型中存在内生性问题。

Wald检验原理:是测量非约束估计量与约束估计量之间的距离，即只需估计非约束模型，所以适用于估计约束模型时比较困难的情形。为了方便讨论，这里将若干约束条件以联合检验的形式给出H0:r(β)=q，构造Wald统计量如下所示:

其中r(β)表示由J个参数约束条件组成的列向量;R(β)=r(β)/;r表示由0组成的列向量;表示非约束模型的参数估计量;^V是^β的方差协方差矩阵。在约束条件成立的条件下，上述构造的Wald统计量渐近服从χ2(J)分布，其中J表示被检验的约束条件个数。

LR检验的基本思想:如果原假设H0对于模型的约束是有效的，那么施加相应的约束不应该使模型似然函数的最大值显著减少。也就是说，LR检验的实质是比较有无约束条件下似然函数的最大值，用二者之间的比值构造LR统计量为:

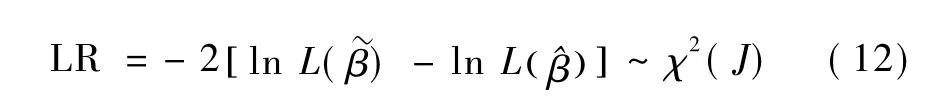
LM检验的判定依据:相对于约束模型估计的残差平方和，无约束模型估计的残差平方和是否显著减少;如果无约束模型估计的残差平方和显著减少，则表明约束条件无效，即拒绝原假设 H0。该检验只需要估计约束模型，无须估计无约束模型，并且在原假设成立的条件下，该统计量也渐近服从χ2(J)分布。设定I()为信息矩阵，其逆矩阵为的方差协方差矩阵，则LM统计量形式为:

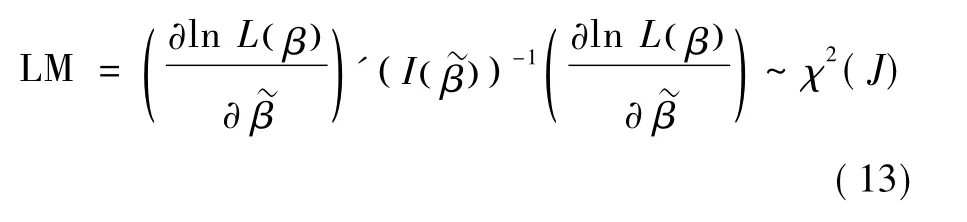
三、蒙特卡洛模拟实验

(一)实验设计

本文探讨包含多项分布内生变量计数模型的两阶段估计方法的有限样本性质，所有模拟计算均由软件Stata13实现。所设计实验的数据生成过程(Data Generate Process，DGP)，具体可分为如下几个步骤:

第一步，利用多项选择Logit模型生成个体i的预期效用(EVi)，并基于此在三个选项集(j=0，1，2)中进行选择决策。设定个体i选择选项j的预期效用按如下形式生成:

其中 obsi～i．i．d．N(0，1);inst1i和 inst2i代表工具变量，inst1i是由服从(0，1)的均匀分布生成的虚拟变量 I［U(0，1) ＜ 0．5］，inst2i～ N(0，1);qi1和 qi2均服从相同的logistic分布，且相互独立。

第二步，如果个体i在选项j上获得的预期效用值(EVij)最大，那么个体 i的选择结果所对应的虚拟变量dij取值为 1，否则取值为 0;若EVi1=max(EVi0;EVi1;EVi2)，那么di1=1，否则di1=0。

第三步，计数因变量yi服从负二项分布，可以通过泊松分布以伽玛分布为权重的连续混合分布抽样获得，其混合概率密度函数为:

其中 Γ(·) 表示伽玛积分;vi～ Gamma(φ，1/φ)。考虑到计数变量的取值具有非负、离散和过度分散的特点，设定两个数据生成过程(DGP1和 DGP2)，其分散系数φ分别设定为1和3，φ值越小表示计数数据越分散。

第四步，设定yi的条件均值μi为常用的指数函数形式为:

其中k为一常数，DGP1和DGP2中分别设定取值为1和 －1。内生性是通过生成并在多项选择和计数模型的生成方程中加入满足特定概率分布的潜在因子qij来完成的，设定 λi1= －0．1、λi2= －0．5;若 λi1=λi2=0，表明潜在因子 qij未进入计数数据均值方程，即内生性问题不存在。

为考察不同估计方法对模型参数估计的实际影响，采用如下五种估计方法对上述计数模型进行估计:

第一种，真实模型(True model，即数据生成过程反向)的极大似然估计;第二种，简化模型(Nave model，即排除潜在因子影响)的极大似然估计;第三种，2SLS;第四种，2SPS;第五种，2SRI。为了比较这些估计方法的优劣，构建了三种衡量指标:平均偏差、方差、均方误差，其中平均偏差是用来观察估计方法的准确性，表示模拟实验中估计参数与真实参数之间的误差平均值;方差为模拟中估计参数的方差，用来观察估计方法的稳健性;均方误差为参数估计值与参数真值之差平方的期望值，用来衡量估计参数与真实参数间的平均绝对偏离程度。在每种估计方法的讨论中，还分别将行为方程设定为负二项回归方程和泊松回归方程，前者是计数模型的正确设定，而后者的设定则违背了计数数据分散的性质，但选用泊松分布能够更好地观察不同方法在错误设定下的具体表现。考察不同估计和检验方法受样本容量的影响，在每个数据生成过程中均选择样本容量分别为 N=300、2 000、5 000，模拟次数为5 000次。根据不同的估计结果，又进一步考察了Wald、LR、LM三种检验方法在检验模型内生性问题时的有效性。

表1报告了虚拟变量dij和计数因变量yi的描述性统计结果。由表1可以看出，在不同的数据生成过程中，dij的边际概率分布是不变的;从yi的均值和方差来看，与DGP2相比，由DGP1生成计数数据yi的“过度分散”特征更为明显;同时，由DGP2生成的yi还显示出了“超额零”的情形。

表1 虚拟变量和计数因变量的描述性统计表单位:%

(二)估计方法的比较分析

1．计数数据的概率分布被正确设定(即行为方程被设定为负二项回归模型)的情形。表2给出了在两种数据生成过程中内生虚拟变量系数(γ1和 γ2)的估计结果，其中 2SRI(R)和 2SRI(S)分别表示在2SRI方法第一阶段估计残差的两种形式:原始残差和标准化残差，其结果表明了这五种估计方法在DGP1和DGP2中的表现基本相似:其一，真实模型的极大似然估计表现最好，并且参数估计结果随样本容量的增加而更加准确，这与笔者的预期相一致;其二，忽略了内生性简化模型的极大似然估计结果却显示了较大的估计偏差，尽管方差和均方误差相对较小，但平均偏差很大且符号为负，说明系数估计值均小于其真值，甚至对γ2会给出符号相反的估计值，而且这种估计偏差不会随样本容量增大而显著减小，可见在估计模型时忽略内生性问题会导致严重的估计偏差，从而得到错误的估计结论;其三，在三种样本容量条件下2SPS和2SRI方法的平均偏差均小于简化模型的极大似然估计，但与真实模型相比仍有较大偏差，但平均偏差、方差和均方误差三个衡量指标会随着样本容量增大而减小，这说明两阶段方法估计在大样本的情况下表现更优;其四，采用标准化残差的2SRI方法，在三种衡量指标上都要优于使用原始残差的2SRI方法和2SPS方法。

为更好地评价上述估计方法，参考Geraci等的做法［9］，本文还构造了一种综合了两个系数估计误差的合成指标——总体误差，其定义为每次模拟中两个参数估计误差的绝对值之和。图1绘制了不同DGP和样本容量下的总体误差概率密度图，并在图中给出了不同情形下的总体误差均值。可以看到，总体误差均值在2SRI(S)、2SRI(R)、2SPS之间存在如下关系:2SRI(S)＜2SRI(R)＜2SPS，表明 2SRI(S)在估计方面更具有优势，这与表2的结论一致。同时，在计数数据更为集中(即DGP2)的情况下，两阶段估计方法的估计总体偏差相对更小，估计结果也相对更好。

表2 基于负二项回归模型估计的模拟结果表

图1 基于负二项回归模型估计的总体误差概率密度图

2．计数数据的概率分布被错误设定为泊松分布 的情形。表3给出了模型被错误设定下各种估计方法的衡量指标，其结果表明:与正确设定的情形相比，每种估计方法在错误设定下的估计偏差都有不同程度的增大，但由DGP2生成的计数数据相对更为集中，所以泊松分布错误设定下估计方法的表现要优于DGP1。尽管如此，错误设定下的真实模型的极大似然估计仍然给出了可靠的估计结果，而简化模型的估计结果还是存在很大的平均偏差。同时，表3还给出了忽略模型非线性的2SLS的估计结果。笔者发现，由于忽略了模型的非线性，2SLS的参数估计结果具有很大的平均偏差、方差和均方误差，这说明2SLS方法并不适合估计非线性计数模型，而2SPS和2SRI则给出了相对较小的估计偏差，其中采用标准化残差的2SRI方法的优势更加明显一些。

图2 基于泊松回归模型估计的总体误差概率密度图

表3 基于泊松回归模型估计的模拟结果表

MSE 6．828 5．384 1．365 1．077 0．573 0．494 6．857 7．311 1．069 0．812 0．504 0．417

同样地，在图2中绘制了错误设定下的2SRI和2SPS估计的总体误差的概率密度图。图2连同表3和表4都印证了使用标准化残差的2SRI方法的优越性。该方法估计参数的参数方差，均方误差和总体误差都要小于其他两种方法，展示出更好的稳定性和准确性，这说明已经发现的2SRI(S)在正确设定下的较优表现在泊松错误的设定时仍然成立。然而，一个与正确设定下不同的结论是，在错误设定下2SPS和2SRI(R)两种估计方法的四种衡量指标都很相近，说明使用原始残差的2SRI方法相较于2SPS的优势在错误模型设定下被严重削弱，两者没有明显的优劣差别。综上可以看出，如果忽略模型的内生性问题和错误设定计数变量的概率分布都会导致严重的估计偏差，但2SRI方法具有相对更为准确和稳定的优势，而且采用标准化残差的2SRI方法要比原始残差表现得更好。

(三)内生性检验方法的比较分析

通过上述估计方法的模拟实验结果表明，在估计包含多项分布内生变量的计数模型时，2SRI方法具有明显优势。下面将基于2SRI方法，利用蒙特卡洛模拟实验，从水平扭曲和检验功效两个方面考察计量经济学中常用的三种检验方法——Wald、LR、LM检验方法的表现，包括检验方法的有效性、模型错误设定对检验效果的影响等。表4～6报告了在不同样本容量和数据生成过程中，基于负二项分布设定的外生性检验的拒绝概率，其结果显示在负二项分布的正确设定下，三种检验方法的检验水平与名义显著性水平均相差不大，表明检验统计量具有合理的检验水平性质。当样本容量为N=300时，三种检验方法的功效都比较小，但随着样本容量的增加，三种检验方法的功效也逐渐趋近于1，这表明在实际应用时，研究者应尽可能采用较大容量样本来检验模型的内生性问题，以保证检验结果的可靠性。同时还发现，与采用原始残差的2SRI方法相比，基于标准化残差的2SRI方法进行的内生性检验方法的功效会有所提高。

表4 基于负二项回归模型的外生性检验拒绝概率表(N=300)

表5 基于负二项回归模型的外生性检验拒绝概率表(N=2 000)

表6 基于负二项回归模型的外生性检验拒绝概率表(N=5 000)

当计数数据被错误设定为泊松分布时，同样模拟了三种检验方法的外生性检验拒绝概率(见表7～9)，其结果显示:由于忽略了数据的过度散布特征，Wald和LR检验方法均发生了严重的水平扭曲现象，远大于名义检验水平值，同时二者的检验功效相对较高，并随着样本容量增大而增大，但二者的检验水平扭曲程度并未明显减小;LM检验水平扭曲较小，始终比较接近于名义水平值，但其检验功效偏差较大，随着样本容量的增加，三种方法的检验功效均接近于1;同时，DGP2的模拟检验结果总体要优于DGP1，这主要是因为由DGP2生成的计数数据的过度散布程度相对较小，所以三种检验方法在样本容量为2 000和5 000时都显示出合理的检验水平与功效。

表7 基于泊松回归模型的外生性检验拒绝概率表(N=300)

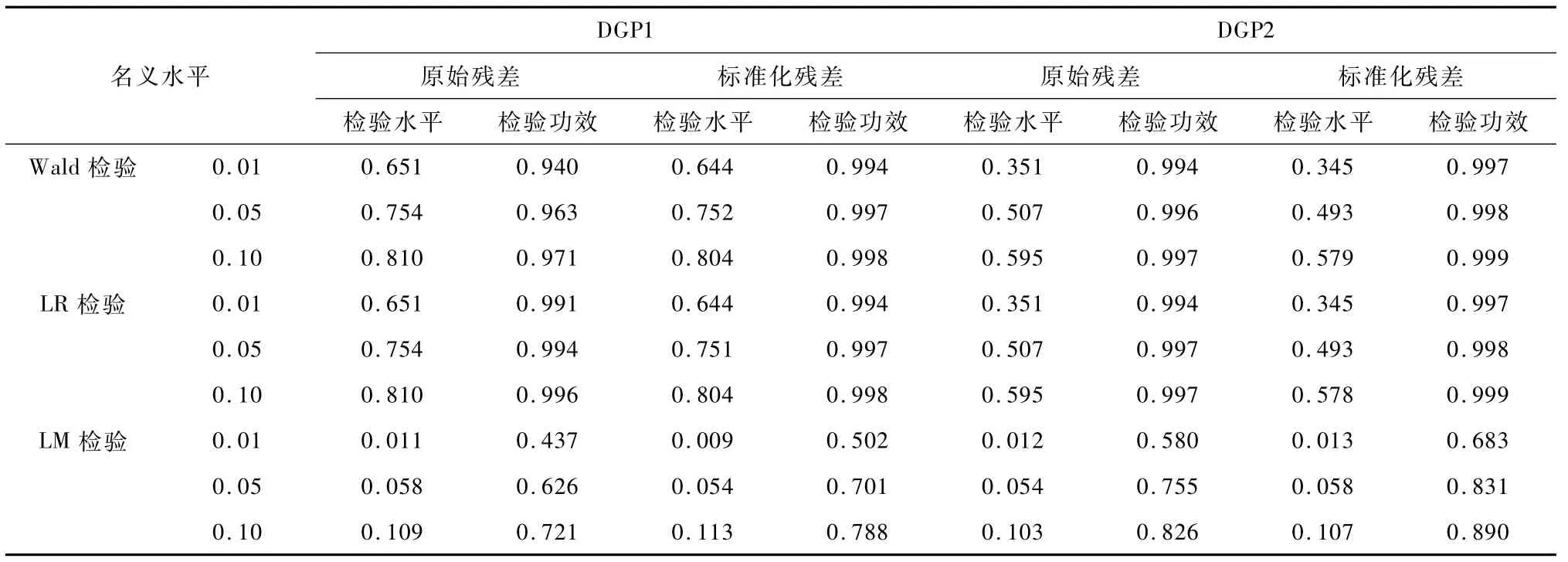
表8 基于泊松回归模型的外生性检验拒绝概率表(N=2 000)

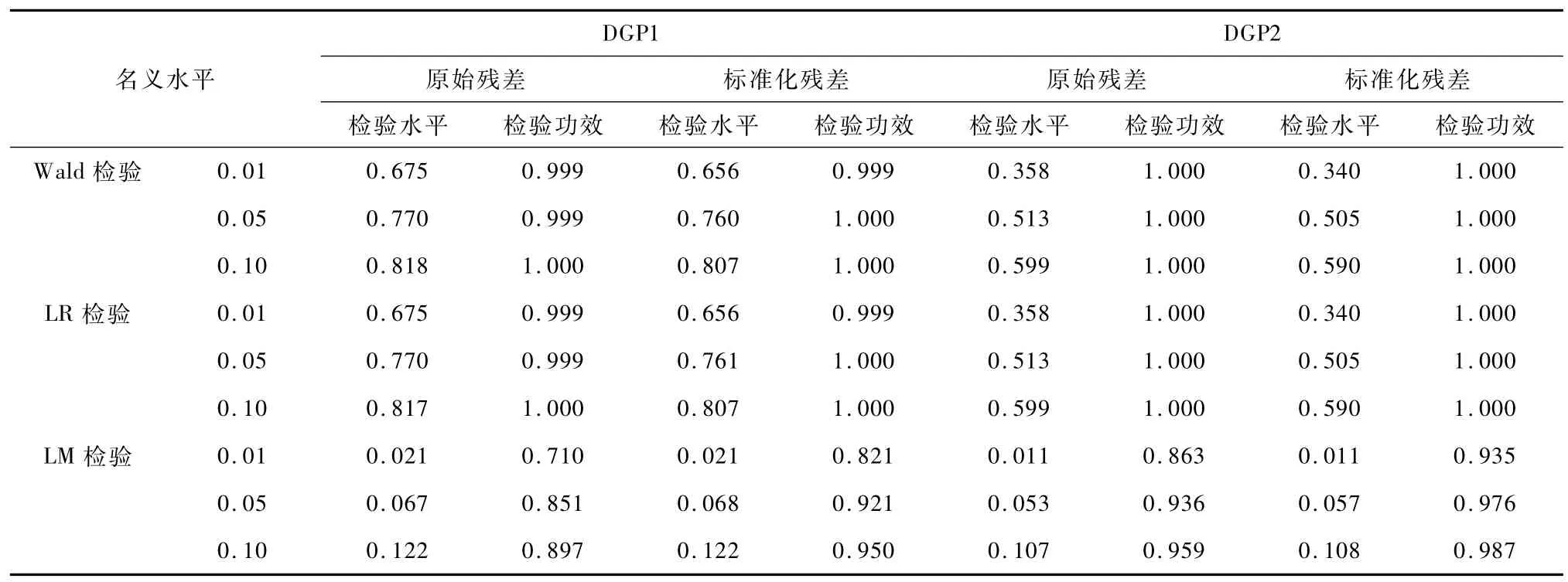
表9 基于泊松回归模型的外生性检验拒绝概率表(N=5 000)

在2SRI方法的第一阶段中，关于残差定义有两种方法:原始残差和标准化残差，为探讨不同的残差定义对三种检验方法效果的影响，绘制了基于不同名义水平和两种残差定义的检验功效对比图(见图3)。从图3中可以看到，在不同的数据生成过程中，三种检验方法在标准化残差定义下均显示了更大的检验功效，尤其是在名义水平小于0．10时。图4展示了在模型被误设为泊松分布时的情形，结果与图3相似，无论模型是否被正确设定，标准化残差处理都会使内生性检验的结果相对更有效。

进一步，基于前文2SRI方法的模拟情况，把第一阶段生成的误差项(即不可观测的潜在因子qi1和qi2)和两种定义下得到的残差进行对比分析，以探究采用标准化残差的2SRI方法表现稳健的原因。图5分别绘制了生成的潜在因子对原始残差和标准化残差进行回归估计的拟合图以及三者的概率分布图，其结果表明与原始残差相比，标准化的残差更好地拟合了潜在因子的可能取值范围，而且从三者的概率密度曲线上来看，对第一阶段估计的残差结果进行单位方差标准化增大了残差的方差，从而能够更好地近似潜在因子误差项，并据此得到更有效的内生性检验结果。

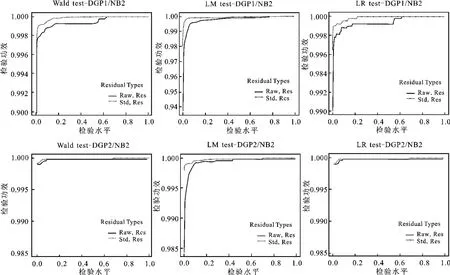
图3 基于两种不同残差定义和负二项分布设定的检验方法功效表现图(N=5 000)

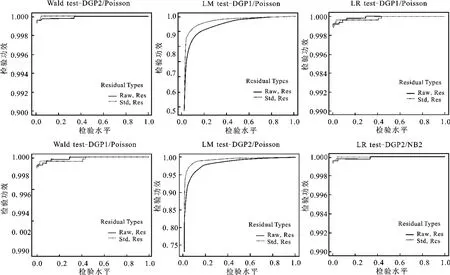
图4 基于两种不同残差定义和泊松分布设定的检验方法功效表现图(N=5 000)

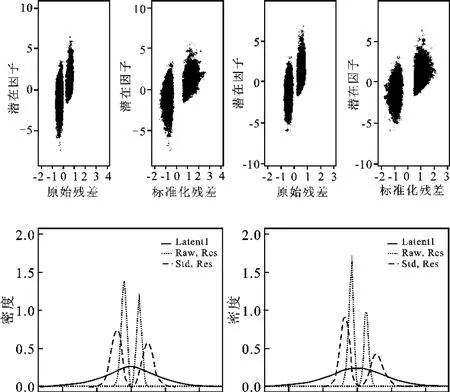
图5 潜在因子和估计残差的拟合图与概率分布图

四、结 论

本文通过蒙特卡洛模拟实验，在数据分布特征、模型设定和样本容量等不同情形下，研究包含多项分布内生回归元计数模型的两阶段估计方法(2SLS、2SPS、2SRI)的表现，并从水平扭曲和功效两个方面评价 Wald、LR、LM三种内生性检验方法的有效性。蒙特卡洛模拟实验的数据生成过程，主要包括离散选择模型、内生性问题的处理以及计数数据的随机抽样，大量模拟结果显示:在忽略模型非线性形式、内生性或者错误设定计数数据分布特征时，2SLS和2SPS会导致较为严重的估计偏差，但2SRI估计量则具有良好的有限样本表现，而且采用标准化残差定义的方法可以使2SRI方法的估计结果更加准确稳定;蒙特卡洛模拟结果进一步表明，基于2SRI估计方法的三种内生性检验方法，在计数数据分布设定正确时都具有合理的实际检验水平和功效，但在忽略计数数据过度分散特征时，Wald和LR检验会发生严重的水平扭曲，而LM检验统计量会更有效;同时，在内生性检验的模拟实验中，本文还发现基于标准化残差的2SRI估计可以使三种检验方法都获得更大的检验功效，即减小了第二类错误的发生概率，并通过对生成潜在因子与两种定义残差进行比较分析，发现标准化定义的残差方差要大于原始残差，能够使其更好地近似生成离散选择模型中的潜在因子。因此，基于标准化残差定义的相关估计和检验方法在有限样本下更加有效。