基于主成分及密切值对比的班级学习情况分析

张鸿睿

（三峡大学 土木与建筑学院，湖南吉首 443000）

现在的教学工作者和教务管理者，面对学生的各种成绩数据，大多数管理者只停留在单一的成绩查询上，导致许多数据资源的浪费。如何准确定量描述一个班的整体学习成绩情况，科学合理地评价班级学生的成绩情况和教学工作中存在的问题，成为了教育工作中普遍面临的难题。

1 问题分析

班级整体成绩情况排序可以由多个评价标准进行综合评价，标准可以有：表示班级总体考试水平的成绩均值；表示班级学习分化程度的成绩标准差；表示班级每位同学在年级排名的平均排名的班级均排名等，为使所有指标保持同向性，即指标值越大班级整体情况越好，需对做取负处理或归一化处理。而这些指标中不可避免地存在一些联系，为解决这一问题，可以选用主成分分析法以最少的信息丢失为前提，将众多的原指标综合成较少几个综合指标。而后验证主成分分析模型所得结果的准确性采用基于熵权的改进密切值模型从新计算班级排名。

2 模型建立

班级整体成绩情况排序可以由多个评价标准综合评价，在本题中班级整体成绩的评价标准可以有：

X

成绩均值，表示班级总体考试水平，均值越大班级整体情况越好；

X

成绩标准差，表示班级学习分化程度，标准差越小班级整体情况越好；

X

班级均排名，即班级每位同学在年级排名的平均排名，排名越靠前班级整体情况越好；

X

班级占年级前50名人数，人数越多班级整体情况越好；

X

班级占年级前100名人数，人数越多班级整体情况越好；

X

班级占年级前150名人数，人数越多班级整体情况越好；

X

班级优秀率，即班级优秀成绩人数占年级人数的比率，比率越大班级整体情况越好；

X

班级及格率，即班级及格成绩人数占年级人数的比率，比率越大班级整体情况越好。为使所有指标保持同向性，即指标值越大班级整体情况越好，需对

X

、

X

做取负处理。为处理这些两两指标中存在一定联系的综合评价类问题，可以选用主成分分析法以最少的信息丢失为前提，将众多的原指标综合成较少几个综合指标。

2.1 主成分评价模型的建立

在实际生活中，每个指标的量纲均不相同，所以在计算之前应先消除量纲的影响，即需对原始数据标准化，做如下变换：

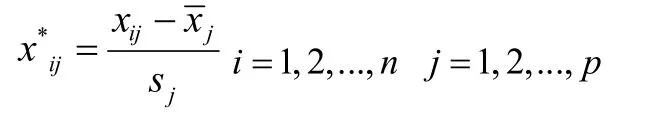
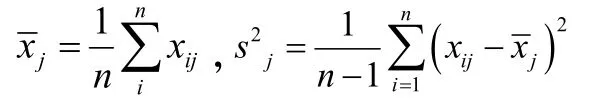
2.1.1 计算协方差矩阵

2.1.2 求出协方差矩阵的特征

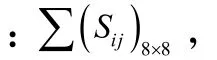
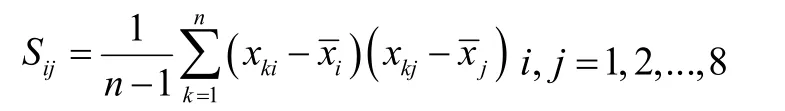
λ

值及相应的正交化单位特征向量

a

然后，根据主成分的方差（信息）贡献率用来反映信息量的大小。其中，

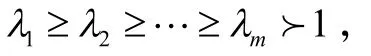
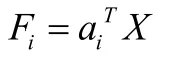
α

的计算表达式如下：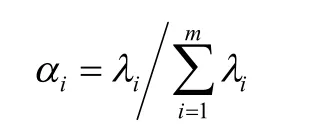

2.1.3 选择主成分

当累计贡献率大于85%时，就认为能足够反映原来变量的信息，对应的

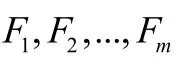
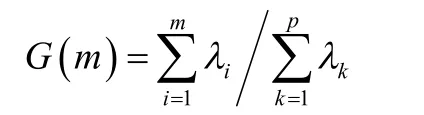
m

就是抽取的前

m

个主成分。

2.1.4 计算主成本荷载

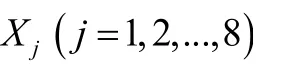
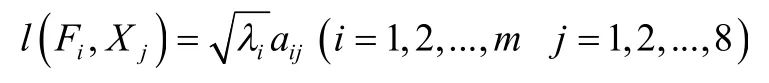
2.1.5 计算主成分得分

计算成绩样本数据在

m

个主成分上的得分如下：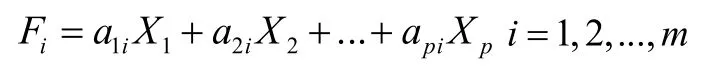

2.1.6 计算主成分权重

计算样本在

m

个主成分上的权重：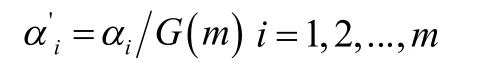

2.1.7 计算总评分

根据上述各个样本在

m

个主成分上的得分以及权重计算在综合指标下的总评分，得到结果如下：

最终，根据

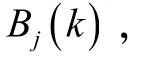
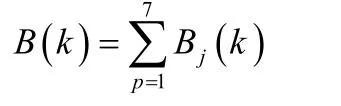
Borda

数大小进行排序便得到了各班近七次考试的综合排名。

2.2 基于熵权改进密切值模型的建立

由于主成分分析模型在处理时对多个主成分进行加权综合会降低评价函数区分的有效度，且该方法易受指标间的信息重叠影响。为验证主成分分析模型所得结果的准确性采用基于熵权的改进密切值模型从新计算班级排名。

由于熵权值对样本数量存在较高要求，即若样本数量不够就无法很好描述指标离散性。为增加样本数量将每个班7次考试的成绩当作7个班一次考试的成绩，这样样本数量就达到了42个。具体步骤如下：

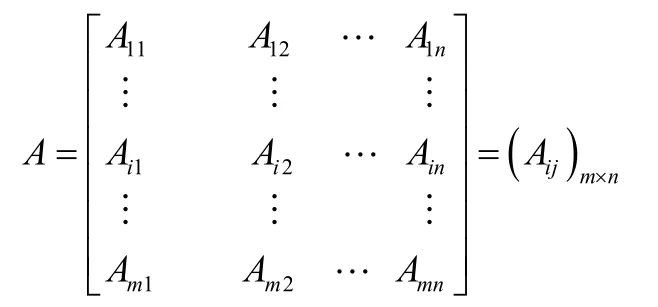
2.2.1 建立原始数据指标矩阵

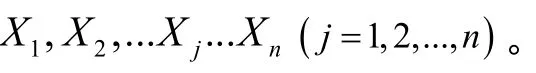
2.2.2 有量纲矩阵模型的规范化

由于初始矩阵中各评价指标的量纲、数量级及指标优劣的取向存在较大差异，故需对初始矩阵数据做规范化处理。模型中采用改进后的目标差值率法进行规范化处理公式如下：

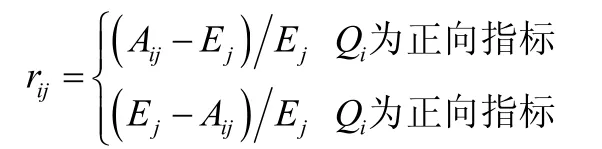
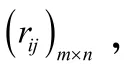
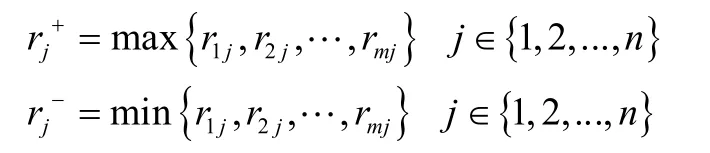
2.2.3 构造虚拟的最优情况班级和最劣情况班级

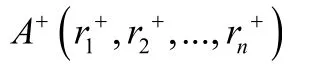
2.2.4 用熵权值法确定各评价指标权重

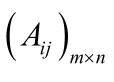
由此得到标准化矩阵：

根据斯梯林公式计算，可得第

j

项指标的信息熵值

e

为：

其中，常数

k

与系统样本数

m

有关，其表达式为：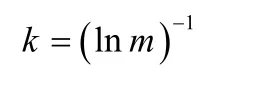

第

j

项指标的信息效用价值取决于该指标的信息熵

e

与1的差值

h

，则第

j

项指标的权重为：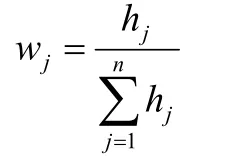

2.2.5 计算密切值

则可得最优密切值为：

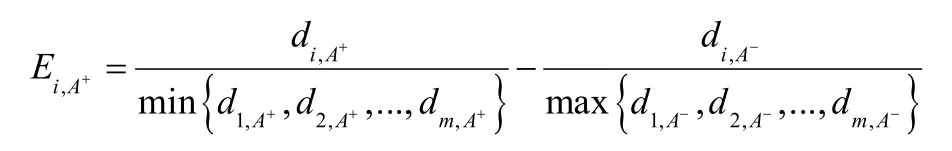
2.2.6 改进密切值法进行班级整体成绩评价原则

最后，由于所得结果是虚拟42个班成绩情况，将其中每个班级的七次考试情况相加便得到该班级近期几次考试总体情况。因此，总指标值越小，班级总体成绩越好，反之越差。

3 模型的求解

在实际生活中，每个指标的量纲均不相同，所以在计算之前应先消除量纲的影响，即需对原始数据标准化，利用主成分分析模型求得各成分的权重计算班级每轮考试的总评分结果如表1。

表1 各班每次考试成绩的综合评价结果

如1表可知，每轮考试的总评分越大，说明本次考试班级的成绩越优秀。同时，直观的观察到1班和6班在7次考试中的总评分都是大于零，相对于其他四个班级成绩更优秀。而2班和4班的总评分均小于零，相比下成绩比较差。

根据上面每班的总评分对每轮考试进行从大到小的排序得到每轮的班级排名。然后，利用决策论中的

Borda

数法来确定得到六个班级在七次考试中总评的

Borda

数。并进行排序，得到了各班近七次考试的综合排名，结果如表2。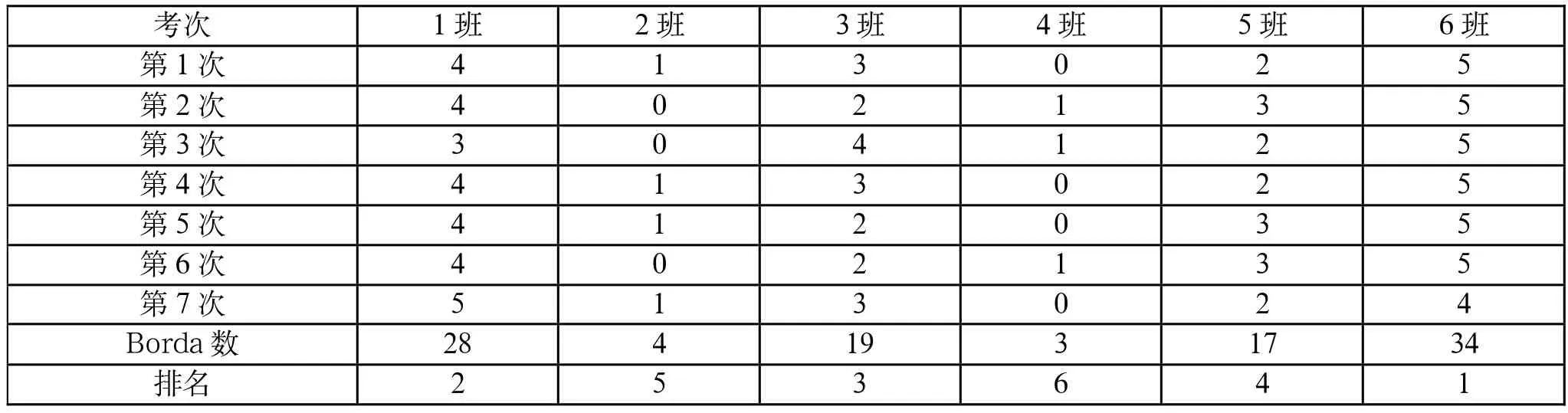

表2 Borda数法的综合排名结果

将班级本次考试年级排名后面的班级个数作为评分，然后累加七次考试评分得到

Borda

数，对其排序得到班级的整体排名。其中，6班和1班分别排在前二名，2班和4班分别排在最后两名，与上文中各班每轮考试的总评分整体分析结果一致，故

Borda

数法得到的排名符合实际。

表3 各班级最优密切值和排名

在上述的排名方法中，各个主成分的权重具有一定的主观想法评价。为了消除主观意向的影响并对上述结果进行验证，利用最优密切值来表示班级综合评价，从而得到各个班级的总排名如表3。

4 结果分析

对于本题，利用主成分分析法得到权重计算总评分，然后用

Borda

数法得到班级排名。这种方法具有一定的主观意识，为了更客观得到班级的排名，利用每个班级的最优密切值进行排序，越小说明班级的成绩越优秀，从而得到班级的排名。两种方法对比发现，各个班级近期成绩排名结果一致，因此，最终排名第一位6班，最后一名为4班，各个班级排名符合客观实际情况。