Group Decision Making With Consistency of Intuitionistic Fuzzy Preference Relations Under Uncertainty

Yang Lin and Yingming Wang

Abstract—Intuitionistic fuzzy preference relation(IFPR)is a suitable technique to express fuzzy preference information by decision makers(DMs).This paper aims to provide a group decision making method where DMs use the IFPRs to indicate their preferences with uncertain weights.To begin with,a model to derive weight vectors of alternatives from IFPRs based on multiplicative consistency is presented.Specifically,for any IFPR,by minimizing its absolute deviation from the corresponding consistent IFPR,the weight vectors are generated.Secondly,a method to determine relative weights of DMs depending on preference information is developed.After that we prioritize alternatives based on the obtained weights considering the risk preference of DMs.Finally,this approach is applied to the problem of technical risks assessment of armored equipment to illustrate the applicability and superiority of the proposed method.

I.INTRODUCTION

GROUP decision making(GDM)is one of the common activities in human daily life,which consists of ranking a given set of alternatives and finding the most preferred one by a group of DMs.During group decision making,each DM is usually asked to provide his/her preference over alternatives and then the preference relations(PRs)are generated automatically[1].In some situations,however,due to the complexity and ambiguity of human mind,fuzzy judgments are often easier than precise ones to make,and DMs usually provide their uncertain and rough PRs in GDM.

As a practical yet valid theory for dealing with uncertain and vague information,intuitionistic fuzzy set(IFS)[2]has attracted many scholars’attention[3]−[6].The advantage of IFS is the capability of describing fuzzy judgments and the capability of representing positive,negative and hesitative viewpoint through membership function[7].When the membership of preference relations is characterized by intuitionistic fuzzy values(IFV,which are the basic components of IFS),the IFPR is generated.Namely,an IFPR is a matrix of values that are created by pairwise comparisons over the given alternatives,and each value implies the preference degree of one alternative over another[8].IFPR has found huge application in various aspects of group decision making[3]−[7],[9]−[15]and increasing attention has been paid to IFPR in recent years.The formal definition of IFPR was given by Szmidt and Kacprzyk[10],who investigated the mechanism of consensus reaching,and examined the extent of agreement in a group of DMs as well[11].Xu and Yager[12]introduce a similarity measure between IFSs and apply this measure in group decision making with consensus analysis based on IFPR.Gong et al.[13]employed the IFPR to study and evaluate the industry meteorological service for Meteorological Bureau of China.Liao and Xu[9]proposed some fractional models for group decision making with IFPRs and applied these models for ranking the main factors of electronic learning.

The consistency,the basic property of IFPR[14],ensures a DM’s judgment yields no self-contradiction during pairwise comparisons with alternatives.How to derive and rank priority weights from an IFPR is considered to be a major issue of use of consistency[15].Generally,existing consistency of IFPR can be classified into two categories,the multiplicative consistency and additive consistency.Numerous ways for acquiring priority weights have been suggested relying on the condition of consistency.Liao and Xu[16]pointed out there is a flaw in additive consistency because it conflicts with the[0,1]scale when used as preference value.In real decision-making problems,however,it is impractical and even impossible for a DM to provide a consistent IFPR due to the limitations of brain and inherent complexity in realistic environments.Since an inconsistent IFPR may lead to reasonable results,it is natural to take the consistency condition into consideration for deriving priority weights.

As to GDM analysis,determining the weights of all DMs is crucial during the process of decision making.Once the weight vector is confirmed,the IFPR of each DM can be directly aggregated to form a collective opinion[17].Xu et al.[3]developed an approach to GDM based on IFPR as well as an approach to GDM based on incomplete IFPR,respectively,where two types of intuitionistic fuzzy averaging operator were defined and employed to aggregate the intuitionistic fuzzy information.Li et al.[18]proposed the intuitionistic fuzzy set generalized ordered weighted averaging(OWA)operator to solve the GDM problem.Liao and Xu[9]develop some algorithms for GDM with multiplicative IFPR via deriving the weight of each DM directly from the individual IFPR.What should be pointed out,however,is that the relative weights of DMs under IFPR environment are determined subjectively in existing literatures.Subjective weights are determined only by DM’s expertise and judgment,otherwise objective weights are obtained via mathematical calculation.The methods of objective weights determination are particularly applicable in cases where reliable subjective weights are not available.

The methods mentioned above have succeeded in solving many GDM problems with IFPR information,however,some limitations in these methods still exist:

1)The relative weights of DMs under intuitionistic fuzzy environments in current literatures are regarded as the same or assigned by subjective weighting methods,which sound somewhat unpractical or even unreasonable in some situations.

2)Current methods[4],[6]−[9],[12],[13],[15],[16]for ranking alternatives in the form of IFPRs are without taking DM’s risk preference(attitude)into account.In practice,various DMs have different preference for risk.That is to say,results may vary in terms of DM’s risk preference for same decision-making problems.

To overcome these drawbacks,in this paper,we developed a new approach for intuitionistic fuzzy GDM based on IFPR with uncertain weights.The motivation of this paper is threefold.First,a new method is suggested for objective weight determination to aggregate each DM’s individual IFPR into a collective one.In this method,relative weights of DMs are derived mathematically from the given preference information and have nothing to do with DMs’subjectivity.Second,we introduce an approach for group decision making by analyzing the multiplicative consistent IFPR.Besides,we review a method that ranks intuitionistic fuzzy weights with considering risk preference of each DM.

The remainder of this paper is organized as follows.In Section II,we briefly review some basic knowledge about the IFS,the IFPR and so on.In Section III,a nonlinear programming model is proposed for exploiting intuitionistic fuzzy weights based multiplicative consistency of individual and group IFPR,respectively;Moreover,a method for deriving relative weights of DMs from IFPRs is developed as well.Section IV investigates two numerical examples using the proposed method and compares three different methods.The paper concludes in Section V.

II.PRELIMINARIES

A.Intuitionistic Fuzzy Preference Relation

Owing to the increasing complexity of the decision-making environment,it is hard and even impossible for DMs,or experts to provide accurate preferences on the pairwise comparison of alternatives.In other words,DMs may not have full confidence in their judgments.In this case,intuitionistic fuzzy sets appear to be a suitable and effective way to deal with such uncertainty and vagueness[16].

Definition 1[2]:Let X=(x1,x2,...,xn)be a fixed nonempty set,an IFS A in X is defined as

which is characterized by a membership function uA:X→[0,1]and non-membership function vA:X→[0,1]with the condition 0≤uA(x)+vA(x)≤1,∃x∈X.The value,πA(x)=1−uA(x)−vA(x)is called the indeterminacy degree or hesitation degree of element x in set A.Particularly,ifπA(x)=0,then the IFS A is reduced to a common fuzzy set.

Definition 2[3]:An IFPR˜R on the set X={x1,x2,...,xn}is characterized by an intuitionistic fuzzy judgments matrix˜R=(j)n×n⊂X×X with˜rij=(uij,vij),where

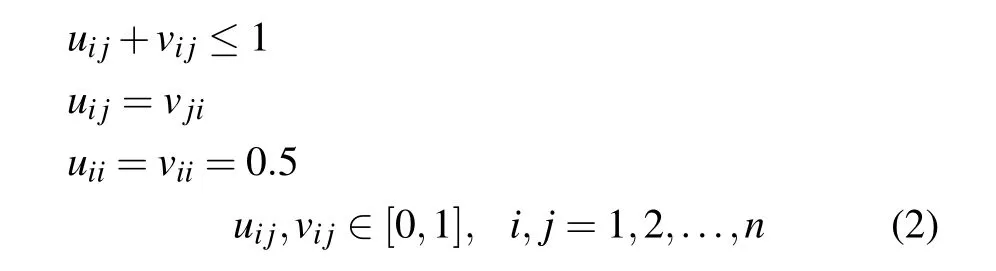
uijis the degree up to which xiis preferred over xj,vijis the degree to which xiis non-preferred to xj,andπij=1−uij−vijis expressed as the indeterminacy degree to which xiis preferred to xj.

Definition 3[4]:Let α=(uα,vα)be an IFV,the score function ofαis defined as

Inspired by the score function,Wang and Luo[19]introduced a formula to rank IFVs,which was in the restricted form as

whereπαis the hesitation degree of elementα;andλ∈[−1,1]is the risk parameter given by the DMs in consensus,reflecting a DM’s attitude towards risk.A smaller value ofλ is accompanied with higher levels of risk aversion.On the contrary,a bigger value means DMs are risk seeking.Whenλis close to 0,it indicates that DMs are risk-neutral and risk aversion(seeking)vanishes.Based on function(4),a ranking method for any two IFVαandβis as below:

1)if Sλ(α)＜ Sλ(β),then α＜β;

2)if Sλ(α)=Sλ(β),then α=β.

B.Multiplicative Consistency of IFPR

Definition 4[16]:An intuitionistic fuzzy preference relation˜R=(˜rij)n×nwith˜rij=(uij,vij)is called multiplicative consistent if satisfying the following condition

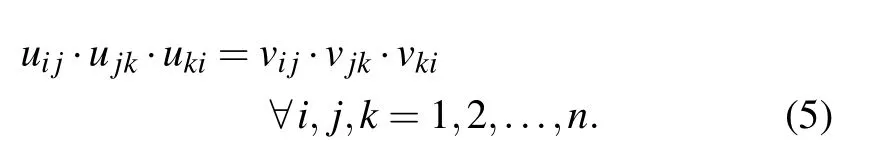
As uij=vjifor any IFPR according to Definition 2,(5)can be rewritten as

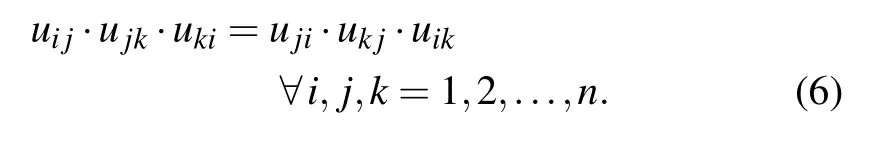
Equation(6)contains only membership degrees of an IFPR,which facilitate our discussion later.

Definition 5[19]:An intuitionistic fuzzy weight vectoris said to be normalized if it satisfies the following conditions:

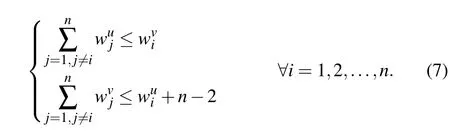
Motivated by the multiplicative consistent FPR and(7),we suppose that

Theorem 1:Assume that the elements of=(ij)n×nare defined by,then˜P is a multiplicative consistent IFPR.

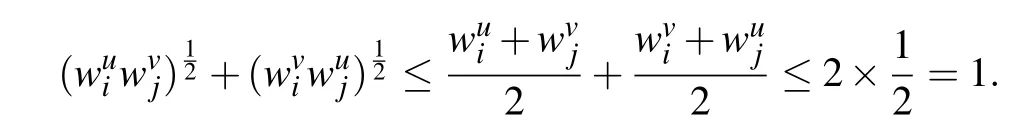
As per Definition 2,˜P=(˜pij)n×nis an IFPR.Moreover,by(8),this gives

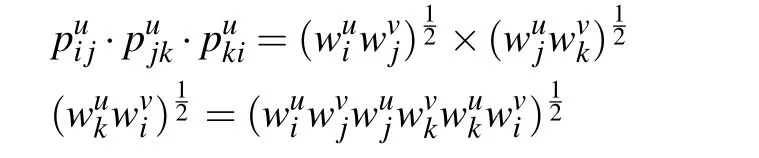
and

Based on Theorem 1,one can easily obtain the corollary as follows.

III.GENERATE THE INTUITIONISTIC FUZZY WEIGHTS BASED ON IFPR

In this section,we propose nonlinear goal programming models for deriving intuitionistic fuzzy weight vector from individual and group IFPRs,respectively.

A.Individual Decision Making With IFPR

Every IFPR built by DMs are expected to be consistent,is the basis for reasonable prioritization as mentioned in Section I.Multiplicative consistency guarantees a DM’s judgment is logical and understandable rather than random.However,in real decision making scenario,it is harsh or sometime impossible for a DM to provide such multiplicative consistent IFPR.Under this case,it is expected that the absolute difference between given IFPRs and the multiplicative consistent IFPRswhich yielded by(9),should be as small as possible.So,we introduce the following deviation variablesφijandϕijto gauge the difference.

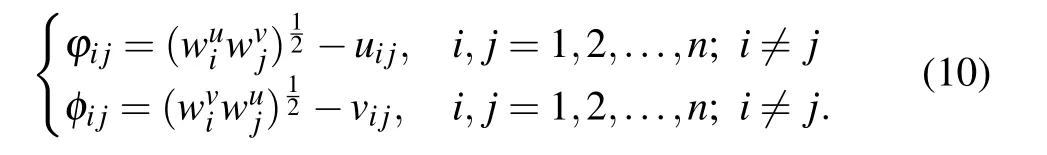
The smaller the absolute difference,the better the results will be produced.This leads to an objective function such that,

As a result,a nonlinear goal programming model can be built to derive the intuitionistic fuzzy weights as follow.

By using some popular optimization tools like MATLAB,WinSQB and so on,model(14)can be solved and an optimal intuitionistic fuzzy weight vector foris obtained.The optimal weight vector is denoted as

Apparent that when J∗=0,we have=0.It implies the IFPRP˜ provided by a DM is multiplicative consistent,and thus,the obtained weight vector is credible.

B.GDM With IFPR Under Uncertain Weights

In real-world situations,decisions are usually made by a group of DMs(or experts)rather than an individual.Hence,group decision making is a more significant topic in current management science that has attracted considerable attention[14],[16],[18],[21],[22].

Let eee ={e1,e2,...,es}be the set of DMs who are invited to express their opinions on alternatives XXX ={x1,x2,...,xn},given that the IFPRgiven by DM ek,k=1,2,...,s is denoted asThe set of weight vector of DMs is ccc =(c1,c2,...,cs),where ckis the kth DM’s weight and satisfying ck＞ 0 andk=1,2,...,s.To determine the weights of each DM is the prerequisite for any GDM problems.A simple way to do that is average assignment if there are no special differences among them.However,a DM may not be able to grasp all aspects of a problem but on some parts of it for which the person is capable[23].So it is natural and reasonable to assume each DM should have a different weight,which is uncertain beforehand and needs to be determined.

In order to determine the weights cknumerically,consider the score function of

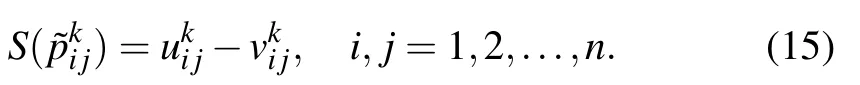
Let

As aforementioned,since the S()can be interpreted as the degree of preference of xiover xjby DM ek,accordingly tikcan be seen as the overall degree of preference of xiover all the other(n−1)alternatives xj(j=1,2,...,n,j/=i).Obviously,greater values of tikare associated with higher levels of preference on xiby a DM[17].Thus,the overall degree of preference of all DMs can be concisely expressed in the matrix format as below:

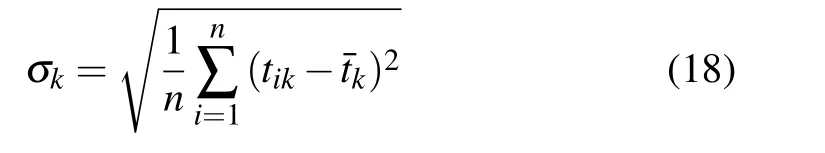
Then(18)can be equivalently written as

Note thatσk=0 if tik=0,i=1,2,...,n.In this case,the removal of tik(i=1,2,...,n)from matrix TTT has little effect on final prioritization.That is to say,the IFPRcan be removed without little impact on group decision making.Therefore,it should be assigned a relatively small weight.Conversely,the greater theσk,the bigger difference among tik(i=1,2,...,n),which implies a stronger preference of the ekdue to(18).From the DM’s perspective,a biggerσkindicates it is more important for group decision making[24],and naturally be assigned a relatively big weight.

Based upon the above analysis,we concluded that greater values of weights should be assigned to those preferences with big deviation.It is reasonable that the relative weights going to be determined should maximize the sum of deviation of the s overall degree of preferences.Thus,a self-evident optimization model to determine the weights of DMs is constructed as follows:

Clearly,model(20)is a single linear optimization problem,which can be easily solved by the Simplex method or some mathematical optimization toolkits.

Determination of the DMs’relative weights is a key issue in any group decision making.Let us now consider a more general version of weight vector ccc =(c1,c2,...,cs),and denote it aswhich satisfies α＞1 be a positive parameter that offers flexible choice of weights for DMs.Thus,model(20)can be converted into the following model:

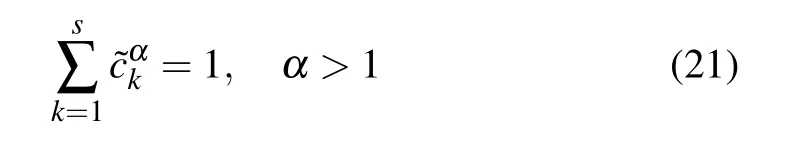
instead of the normalized weight constrainwhere

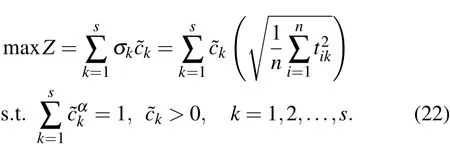
Regarding this optimization model,we have the following theorems.

Proof:Since

taking the partial derivatives of L within˜ckand letting them be 0,yields that

It follows that

Hence,we obtain

After normalization,(28)becomes,

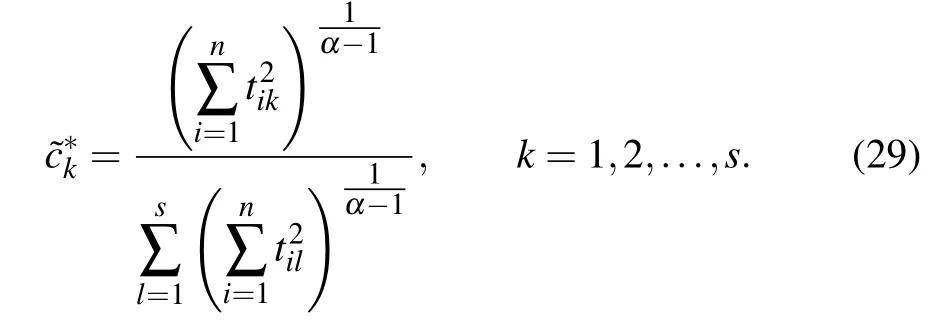
Once we obtain the weight vector of DMs,the IFPR given by each DM can be aggregated for building a collective goal programming model.As aforementioned in Section IV-A,we expect that the deviation between the given IFPRs,as well as the multiplicative consistent IFPRs approach to zero.This idea yields the following deviation variables:

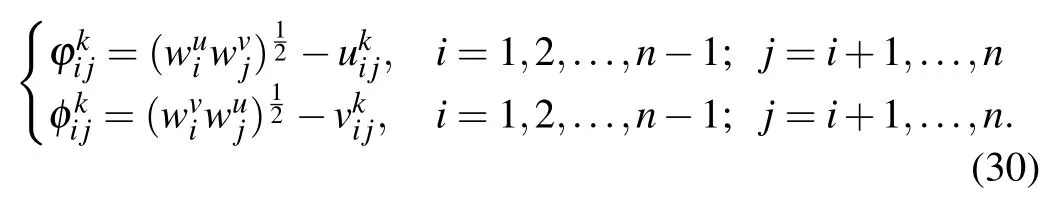
Thus,a group goal programming model was constructed in a similar way of model(14)to derive an intuitionistic fuzzy weight

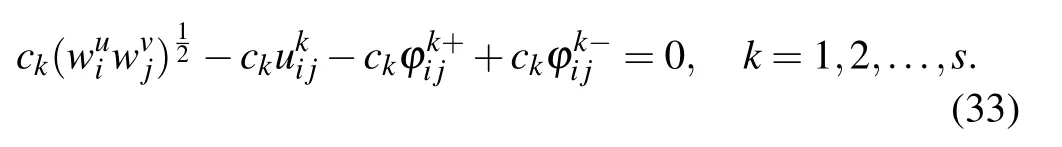
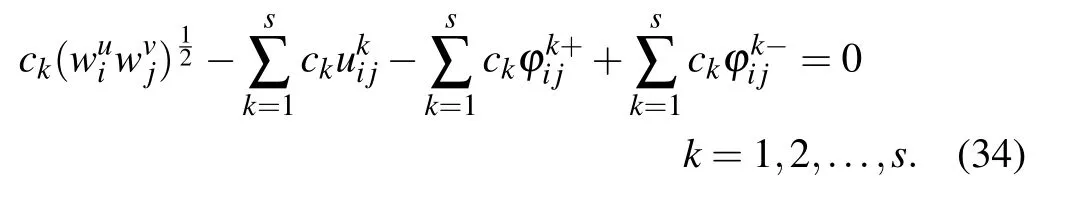
Likewise,we can obtain

TABLE ICOMPARISON FOR PRIORITY WEIGHTS WITH DIFFERENT METHODS

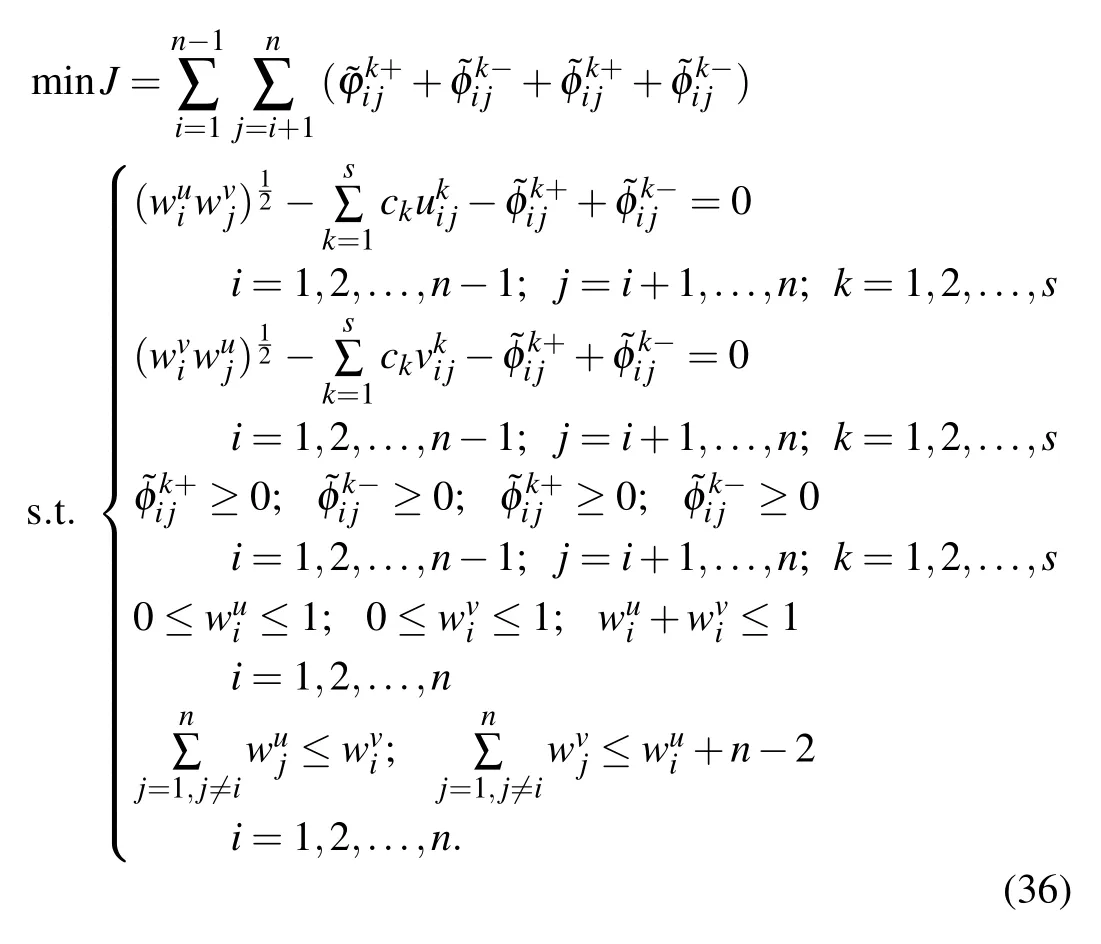
By solving model(35),it gives an overall intuitionistic fuzzy weight vectorfor GDM withObviously,model(35)has less computational complexity as it can be accomplished in linear time.

IV.NUMERICAL ILLUSTRATION

To illustrate the proposed method,two numerical examples are examined to show how to apply it to generate the intuitionistic fuzzy weights from IFPR for prioritization.Meanwhile,a comparison analysis of the obtained solutions with other methods is carried out in this section.

A.Description and Decision Model

Example 1:Consider a DM with risk-attitude representing his/her IFPR over a set of alternatives{x1,x2,x3},which are taken from Wang[15].

It can be checked via(6)thatdoes not satisfy the condition of multiplicative consistent.According to model(14),the goal programming model is built as follow:

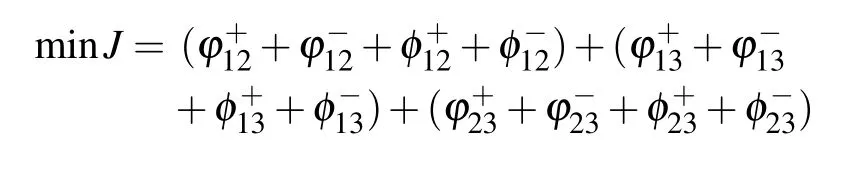
By using Lingo 11 to solve this model,we have the following results:

Therefore,the optimal intuitionistic fuzzy weight vector0.932)).As we knowλ=0,and calculated by(4),we getwhich gives the ranking of x2≻x3≻x1.

Wang[15]used the additive consistency-based method to derive a priority weight vector,and Liao and Xu[16]constructed a fractional programming model to extract priority weights based on multiplicative consistency-based method.Their findings are listed in Table I which led to the same ranking:x2≻x3≻x1as our method does,but with slightly different membership degree of preference.

With the development of weapon and the requirement of modern warfare,many state-of-the-art technologies,Such as Markovian jumping systems,dynamic feedback control[25]etc.,have been applied to military weapons and equipment.In pursuit of high performance of modern weapons,however,there is more risk in their application.That is to say,military high-techs are generally accompanied with higher risk.They are often lacking of necessary and precious data for evaluating associated technological risk,which may cause a serious effect on finalization of the military and industrial products.In this situation,intuitionistic fuzzy value as well as preference relation is a powerful tool in estimating underlying technical risk by experts.

A research institute of Nanjing military region in China planned to have an evaluation of technical risk of a tentative armored vehicle.Three experts e1,e2and e3were invited to join this plan.The research institute had hesitation in determining the weight of each expert owing to lack of cooperation basis.There are four potential risk factors identified by experts for further estimating,which include maturity(x1),complexity(x2),reliability(x3)and prospective(x4)of technology.Each expert ek(k=1,2,3),is asked to have a pair-wise comparison for these factors,resulting in the following intuitionistic fuzzy preference relation(k=1,2,3).

By using(16)and(17),the overall degree of preference of all the experts is denoted by matrix TTT ,as follows:

Based on TTT,the priority weights vector of experts can be derived by(29).Suppose the weight assignment parameter α=2.0,thus the relative weight of each expert can be obtained as:c1=0.381,c2=0.361,c3=0.258.According to model(34),a nonlinear programming model for GDM can be constructed,and solving this model by using Lingo 11 software toolkit,we obtained the optimal intuitionistic fuzzy weights

Consider the experts are all risk-neutral,leads toλk=0,k=1,2,3.As per(4),we can easily getwhich gives the ranking of x1≻x4≻x2≻x3.Hence,the maturity of technology(x1),should be given first priority during the process of technical risk evaluation of armored equipment.

From the results we have,the factor of maturity(x1)ranks first in the risk control process.This is somewhat in conformity with our intuition in that the factor of maturity in any modern military equipment should be placed in a fundamental position.

Remark 1:We compare the results,by varying DMs’risk preference from risk-neutral to risk aversion,and risk seeking as well.Assume that the DMs feel an aversion to factors x1and x2,but in favor of risk-seeking to the two others yet.Given that the risk parameter for each factor after negotiation beλ1= −0.5,λ2=−0.75,λ3=0.8,λ4=0.35.As per(4),it yields that=−0.088,respectively.

As can be seen from Table II,if DMs vary their risk preference,the priorities of these factors are also change.This shows that it is reasonable and necessary to bring the risk parameter into consideration during a GDM course.Besides,it is deserving to point out that these existing methods without considering risk preference are just a special case of our method when risk parameters are all equal to zero.

TABLE IIRANKING RESULTS WITH DIFFERENT RISK PARAMETERS

B.Comparison Analysis

A comparative study was conducted to contrast between our method and other ones.As the same problem of Example 2,we use several different approaches to tackle this problem.To facilitate our analysis,we suppose that all DMs are riskneutral.We use Xu et al.normalizing rank summation method[5] firstly.For simplicity,suppose each DM has the same relative weight and similarly hereinafter.The intuitionistic fuzzy weights produced by this method are=(0.232,0.661),=(0.195,0.697),=(0.169,0.755),=(0.220,0.658),and the values of the corresponding score function are,S()=−0.4748,S()=−0.5566,S()=−0.6307,S(˜w4)=−0.4911.

Secondly,we use the approach in Liao and Xu[16]to derivate the weights of alternative.Then we obtain optimal relative weights such that=(0.432,0.257),=(0.076,0.678),

Moreover,we employ Gong et al.goal-programming-based model[13],which need to transform the given IFPRs into interval FPR before(for more details refer to[13]).By building and solving a goal programming model,we obtain w1=[0.242,0.376],w2=[0.208,0.234],w3=[0.166,0.189],w4=[0.206,0.362].Through the equationwhere w+and w−are upper and lower bounds of a range,these interval-value weights can be transformed into intuitionistic fuzzy weights as−0.50.We show in Table III the ranking order of alternatives obtained by these methods.

V.CONCLUSIONS

In this paper,we have put forward an efficient approach for decision making where preference information on alternatives is IFPRs and is extended to GDM surrounding.The main idea of this method is first to minimize the absolute deviation between the given IFPRs and the converted consistent IFPRs,then the prioritization of alternatives is obtained based on multiplicative consistent constraint.It is necessary to point out that the proposed method is simple and does not need to solve the fractional programming model as Liao and Xu[16]does.Thus,the standard deviation,an index of overall degree of preferences,was defined and adopted to measure the importance of DMs in a group.By minimizing this index,the weights of DMs were determined.Thus,the model was extended from individual to group application by IFPRs aggregation.Specifically,the risk preference of each DM was considered for rank alternatives which makes this approach more general and flexible.In the future,we will improve our approach and apply it to correlated multi-attribute,and dynamic hybrid multi-attribute GDM problems with IFPRs.

TABLE IIICOMPARISON ANALYSIS