Containment Control of Fractional Order Multi-Agent Systems With Time Delays

Hongyong Yang,Fuyong Wang,and Fujun Han

Abstract—In complex environments,many distributed multiagent systems are described with the fractional-order dynamics.In this paper,containment control of fractional-order multiagent systems with multiple leader agents are studied.Firstly,the collaborative control of fractional-order multi-agent systems(FOMAS)with multiple leaders is analyzed in a directed network without delays.Then,by using Laplace transform and frequency domain theorem,containment consensus of networked FOMAS with time delays is investigated in an undirected network,and a critical value of delays is obtained to ensure the containment consensus of FOMAS.Finally,numerical simulations are shown to verify the results.

I.INTRODUCTION

RECENTLY,with the rapid development of network and communication technology,the distributed coordination for networked systems has been studied deeply[1]−[5].Cooperative control of multi-agent systems has become a hot topic in the fields of automation,mathematics,computer science,etc[6]−[10].It has been applied in both military and civilian sectors,such as the formation control of mobile robots,the cooperative control of unmanned spacecraft,the attitude adjustment and position of satellite,and the scheduling of smart power grid systems,etc.As a kind of distributed cooperative control problems of multi-agent systems with multiple leaders,containment control regulates followers eventually converge to a target area(convex hull formed by the leaders)by designing a control protocol,which has been paid much more attention in recent years[11]−[13].

In the complex practical environments,many distributed systems cannot be illustrated with the integer-order dynamics and can only be characterized with the fractional-order dynamics[14]−[16].For example, flocking movement and food searching by means of the individual secretions,exploring of submarines and underwater robots in the seabed with a massive number of microorganisms and viscous substances,working of unmanned aerial vehicles in the complex space environment[17],[18].Cao et al.have studied the coordination of multiagent systems with fractional order[19],[20],and obtained the relationship between the number of individuals and the order in the stable fractional system.Yang et al.have studied the distributed coordination of fractional order multi-agent systems with communication delays[21],[22].Motivated by the broad application of coordination algorithms in fractional order multi-agent systems(FOMAS),the containment control of distributed fractional-order systems will be studied in this paper.

For containment control problems,the current research works are mainly focused on integer-order systems[11]−[13],[23]−[26].In[11],containment control problem for first-order multi-agent systems with the undirected connected topology is investigated,and the effectiveness of control strategy is proven by using partial differential equation method.In[12],second-order multi-agent systems with multiple leaders are investigated,the containment control of multi-agent systems with multiple stationary leaders can be achieved in arbitrary dimensions.In[13],two asymptotic containment controls of continuous-time systems and discrete-time systems are proposed for the multi-agent systems with dynamic leaders,and the constraint condition for control gain and sampling period are given.Considering factors such as external disturbance and parameter uncertainty in[23],the attitude containment control problem of nonlinear systems are studied in a directed network.The impulsive containment control for second-order multi-agent systems with multiple leaders is studied in[25],[26],where all followers are regulated to access the dynamic convex hull formed by the dynamic leaders.

When agents transfer information by means of sensors or other communication devices in coordinated network,communication delays have a great impact on the behaviors of the agents.Now,the influences of communication delays on multi-agent systems have also been paid more attentions[2],[7]−[10]where these research activities on the coordination problem are mainly concentrated on integer-order multi-agent systems.In[24],containment control problem of multi-agent systems with time delays is studied in fixed topology,and two cases of multiple dynamic leaders and multiple stationary leaders are discussed,respectively.As far as we know,few researches have been done on the containment consensus of fractional order multi-agent systems with time delays.

In this paper,the containment control algorithms for multiagent systems with fractional dynamics are presented,and the containment consensus of distributed FOMAS with communi-cation delays is studied under directed connected topologies.The main innovation of this paper is that the distributed containment control of fractional order multi-agent systems with multiple leaders and communication delays is studied for the first time.The research presented in this paper is different from[21],where consensus of FOMAS without leader[21]is much easier than containment control of FOMAS with multiple leaders in this paper.The rest of the paper is organized as follows.In Section II,we recall some basic definitions about fractional calculus.In Section III,some preliminaries about graph theory are shown,and fractional order coordination model of multi-agent systems is presented.Containment control of fractional coordination algorithm for multi-agent systems with communication delay is studied in Section IV.In Section V,numerical simulations are used to verify the theoretical analysis.Conclusions are finally drawn in Section VI.

II.FRACTIONAL CALCULUS

Fractional calculus has played an important role in modern science.There are two fractional operators used widely:Caputo and Riemann-Liouville(R-L)fractional operators.In physical systems,Caputo fractional order operator is more practical than R-L fractional order operator because R-L operator has initial value problems.Therefore,in this paper we will apply Caputo fractional order operator to describe the system dynamics and analyze the stability of proposed FOMAS algorithms.Generally,Caputo operator includes Caputo fractional integral and Caputo fractional derivative.Caputo fractional integral is defined as

where the integral order p ∈ (0,1], Γ(·)is the Gamma function,and t0is a real number.Based on the Caputo fractional integral,for a nonnegative real number α,Caputo fractional derivative is defined as

where p=[α]+1 − α ∈ (0,1]and[α]is the integral part of α.If α is an integer,then p=1 and the Caputo fractional derivative is equivalent to the integer-order derivative.In this paper,we will use a simple notation f(α)to replaceCt0Dtαf(t).Let L(·)denote the Laplace transform of a function,the Laplace transform of Caputo derivative is shown as

III.PROBLEM STATEMENT

Assume that n autonomous agents constitute a network topology graph G={V,E,A},in which V={v1,v2,...,vn}represents a set of n nodes,and its edges set is E⊆V×V.I={1,2,...,n}is the node index set,A=[aij]∈ Rn×nis an adjacency matrix with elements aij≥0.An edge of the diagraph G is denoted by eij=(vi,vj)∈E.Let the adjacency element aij＞0 when eij∈E,otherwise,aij=0.The neighbors’set of node i is denoted by Ni={j∈ I:aij＞ 0}.

Let G be a weighted graph without self-loops,i.e.,aii=0,and matrix D=diag{d1,d2,...,dn}be the diagonal matrix with the diagonal elementsrepresenting the out-degree of the ith agent.L=D−A is the Laplacian matrix of the weighted digraph G.For two nodes i and k,there is index set{k1,k2,...kl}satisfying aik1＞0,ak1k2＞0,...,aklk＞0,then there is an information transmission linked path between node i and k,also we say node i can transfer the information to node k.If node i can find a path to reach any node of the graph,then node i is globally reachable from every other node in the digraph.

Lemma 1[3]:0 is a simple eigenvalue of Laplacian matrix L,and X0=C[1,1,...,1]Tis corresponding right eigenvector,i.e.,LX0=0,if and only if the digraph G=(V,E,A)has a globally reachable node.

Lemma 2[9]:Matrix L+B is a positive definite matrix,where L is a Laplacian matrix of the digraph G=(V,E,A)with a globally reachable node,and B=diag{b1,...,bn}with bi≥0 and at least there is one element bi＞0.

Definition 1:The convex hull of a finite set of points x1,...,xmdenoted by Co{x1,...,xm},is the minimal convex set containing all points xi,i=1,...,m.More specifically,

Recently,fractional order systems have been widely applied in various science fields,such as physics,hydrodynamics,biophysics,aerodynamics,signal processing and modern control.The theories of fractional order equations are studied deeply,and the relationship between the fractional order and the number of agents to ensure coordination has been presented in[19].Assume that Caputo fractional derivative is used to indicate the dynamics of multi-agent systems in the complex environments,the fractional order dynamical equations are defined as

where xi(t)∈ R and ui(t)∈ R represent the ith agent’s state and control input respectively,represents the α (α ∈(0,1])order Caputo derivative.Assume the following control protocols are used in FOMAS

where aikrepresents the(i,k)elements of adjacency matrix A,γ＞0 is control gain,Nirepresents the neighbors collection of the ith agent.

Suppose the multi-agent systems consisting of n1following agents and n2leader agents in this paper,where n1+n2=n.Then,the control protocols of the multi-agent systems can be rewritten as

The systems(3)−(5)can be rewritten as

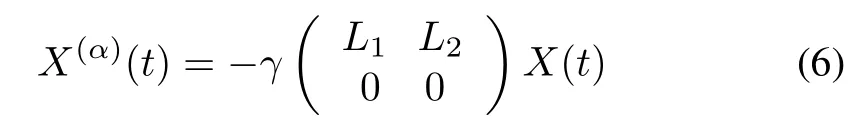
where X(t)=[X1(t),X2(t)]T,X1(t)=[x1(t),x2(t),...,xn1(t)]T,X2(t)=[xn1+1(t),...,xn(t)]T,L1∈ Rn1×n1,L2∈ Rn1×n2.X1(t)is the set of the followers,and X2(t)is the set of the leaders.

Remark 1:Matrix L1=(lik)∈ Rn1×n1satisfying

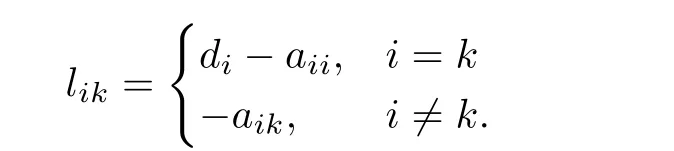
Matrix L2=(lik)∈ Rn1×n2satisfying

Assume the collection formed by leaders is regarded as a virtual node,if one follower agent can connect to some leader,then the follower is connected to the virtual node.

Definition 2:The containment control is realized for the system(3)under certain control input(5),if the position states of the followers are asymptotically converged to the convex hull formed by the leaders.

Assumption 1:For any one follower,there is a directed connected path to the virtual node formed by leaders.

Lemma 3:With Assumption 1,matrix L1is positive definite,andis a non-negative matrix whose entries sum in every row equals to 1.

Proof:From Lemma 2,matrix L1is positive definite matrix.Let L1=dIn1−Q where d is a positive number which is large enough and matrix Q is a non-negative matrix.it has

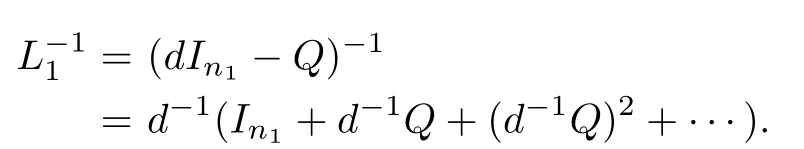
From Lemma 1,Laplacian matrix L will be satisfied with LX0=0,where X0=[1,1,...,1]T∈ Rn×1.Then we have

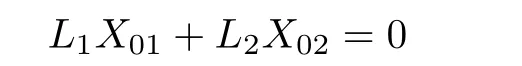
where X01=[1,1,...,1]T∈ Rn1×1and X02=[1,1,...,1]T∈ Rn2×1.Since L1is a positive definite matrix from Assumption 1 and Lemma 2,it has

Theorem 1:Consider a directed dynamic system of n1followers and n2leaders with dynamics(3),whose dynamic topologies are satisfied with Assumption 1.Then the containment control is realized for the FOMAS under certain control protocol(5).

Proof:Based on the system(6),we have

It is known that the fractional differential system(8)is asymptotically stable iff‖arg(spec(L1))‖ ＞ απ/2.Since L1is positive definite matrix,α ∈(0,1],we obtain limt→∞=0,i.e.,

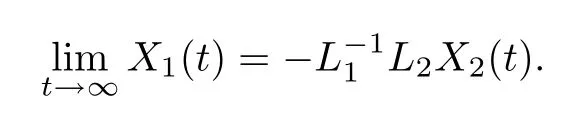
Remark 2:If FOMAS of n agents and n2=1 leaders with dynamics(3),the containment control result in Theorem 1 will become the consensus of multi-agent systems with one leader.

Remark 3:If the fractional order α=1 in FOMAS,the containment control result in Theorem 1 will become that of multi-agent systems with integer-order dynamics[1].

IV.CONTAINMENT CONTROL OF FOMAS WITH TIME DELAYS

In this section,we assume that there are communication delays in the dynamical systems,and containment control of the fractional-order agent systems with communication delays will be studied.Under the influence of communication delays,we can get the following algorithm

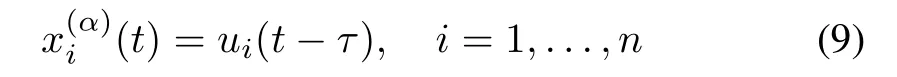
where τ is the communication delay of agent i.Through a simple change we can obtain

Theorem 2:Suppose that multi-agent systems are composed of n independent agents with n1followers and n2leaders,whose connection network topology is undirected with Assumption 1.Then fractional-order multi-agent system(10)with time delays can asymptotically reach containment control,if

Proof:By applying Laplace transformation to system(11),we can obtain the characteristic equation of the system

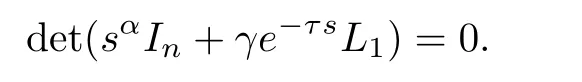
Since the Laplacian matrix L1is symmetrical positive de finite,there is an orthogonal matrix P satisfying L1=PΛP−1,where Λ =diag{λ1,...,λn}with λi＞ 0.Therefore,the root of the characteristic equation is satisfied with s/=0.

When s/=0,let F(s)=det(In+ γs−αe−τsL1),we will prove that all solutions of F(s)=0 have negative real parts.Let G(s)= γs−αe−τsL1,according to the generalized Nyquist criterion,if for s=jω,where j is complex number unit,point−1+j0 is not surrounded by the Nyquist curve of G(jω)’s eigenvalues,then all zero points of F(s)have negative real parts.Let s=jω,we can get

we have the eigenvalues of G(jω)

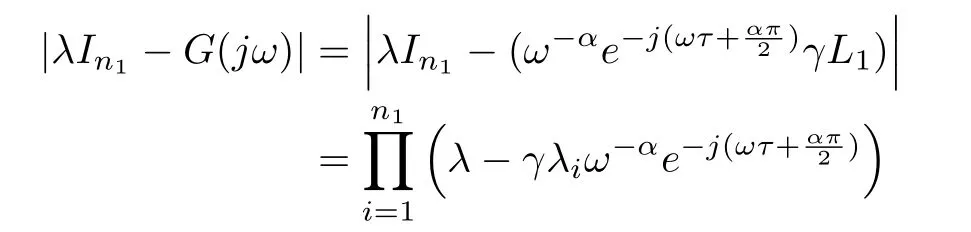
where λiis the eigenvalues of L1.When ω =(2 − α)π/(2τ)the Nyquist curve of G(jω)’s eigenvalues will cross the left of the real axis.If

the point−1+j0 is not surrounded by the Nyquist curve of G(jω)’s eigenvalues.Since fractional order α ∈ (0,1],we obtain

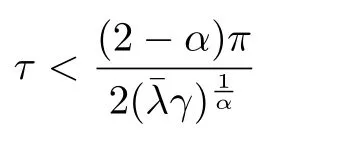
Corollary 1:Suppose multi-agent systems are composed of n independent agents with n2=1 leader,whose connection network topology is directed and symmetrical with Assumption 1.Then FOMAS(10)with time delays can asymptotically follow the tracks of the leader,if

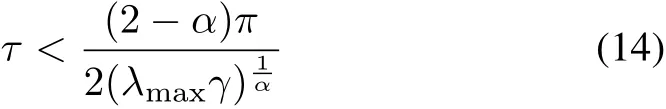
where λmaxis the max eigenvalue of matrix L1.

Corollary 2:Suppose multi-agent systems are composed of n independent agents with n1followers and n2leaders,whose connection network topology is directed and symmetrical with Assumption 1.Then fractional order multi-agent system(10)with time delays can asymptotically reach consensus with α=1,if

where λmaxis the max eigenvalue of matrix L1.

Remark 4:If the fractional order α=1 in FOMAS,the containment control result in Theorem 2 will become that of delayed multi-agent systems with integer-order dynamics.

Remark 5:The consensus result in Corollary 2 for γ=1 is in accord with that of delayed multi-agent systems with integer-order dynamics in[2].

V.SIMULATIONS

Consider the dynamic topology with 5 followers and 3 leaders(illustrated as A1,A2,A3)shown in Fig.1,where the connection weights of each edge is 1.Suppose the fractional order of the multi-agent system α=0.9.

Fig.1.Network topology of multi-agent systems.

From the communication topology of FOMAS,the system matrix can be obtained

Assume that the control parameter of system is taken γ=1.0.The initial positions of followers are taken as x1(0)=(1,1),x2(0)=(1,2),x3(0)=(2,1),x4(0)=(2,3),x5(0)=(3,2),respectively.The initial positions of leaders are taken as A1(0)=(4,4),A2(0)=(4,6),A3(0)=(6,4).Fig.2 shows the state trajectories of FOMAS without time delays,where the followers have converged into the convex hull formed by the leaders.

Next,we will verify the results of FOMAS with time delays.The maximum eigenvalue of L1is 4.618.According to the constraints of Theorem 2 in this paper,the allowed upper bound of the delays is 0.3157.Let τ(t)=0.20 is the time delay of multi-agent systems.The initial parameters in the experiments are same as the simulation without time delays.Fig.3 shows the state trajectories of FOMAS with time delays,where the followers have converged into the convex hull formed by the leaders.

VI.CONCLUSION

This paper studies containment control of fractional multiagent systems with communication time delays.Containment consensus of multi-agent systems with directed network topology is studied.By applying the stability theory of frequency domain,FOMAS with delay is analyzed,and the relationship between the control gain of multi-agent systems and the upper bound of time delays is derived.Suppose the orders of the fractional dynamical systems are all 1,the extended conclusion in this paper is the same with ordinary integer order systems.The containment control of fractional order multiagent systems with dynamical topologies and linear time varying(LTV)systems will be investigated in the future works.

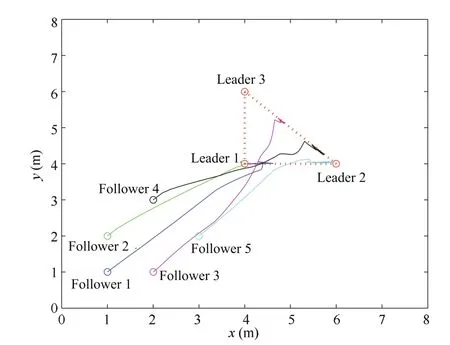
Fig.2.Moving track of FOMAS without communication delays.

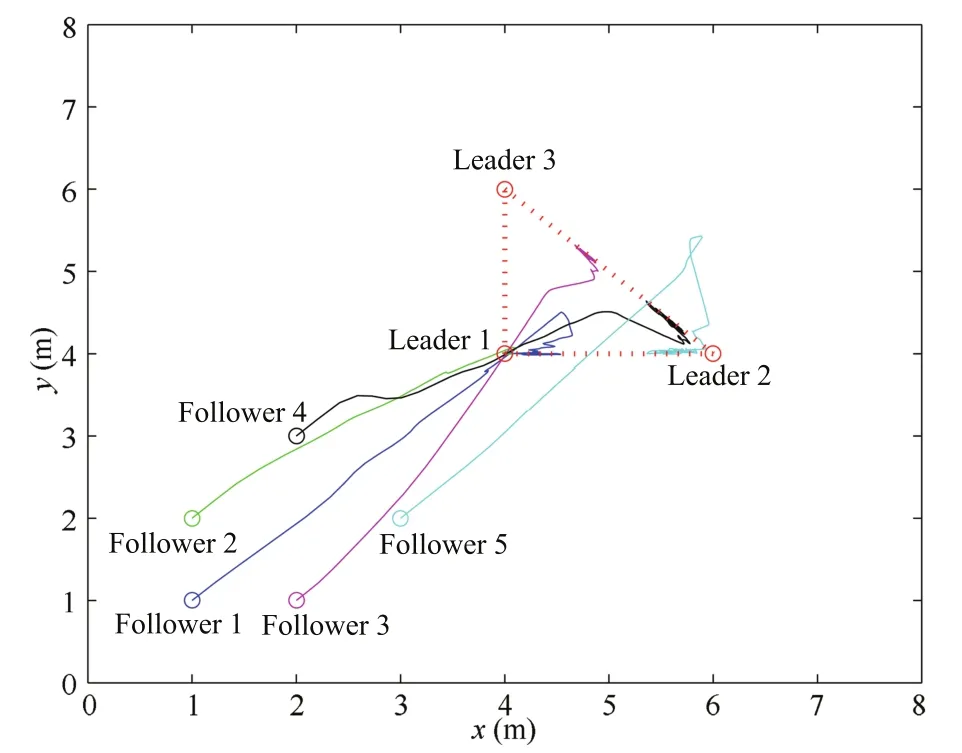
Fig.3.Moving track of FOMAS with communication delay τ=0.20.

Then,we will enlarge the time delays in FOMAS.Let τ(t)=0.30 is the time delay of multi-agent systems in the experiments.Fig.4 shows the running trajectories of FOMAS.The followers can asymptotically converge to the dynamic region formed by three leaders,i.e.,the containment control of fractional-order multi-agent systems with time delays can be achieved.

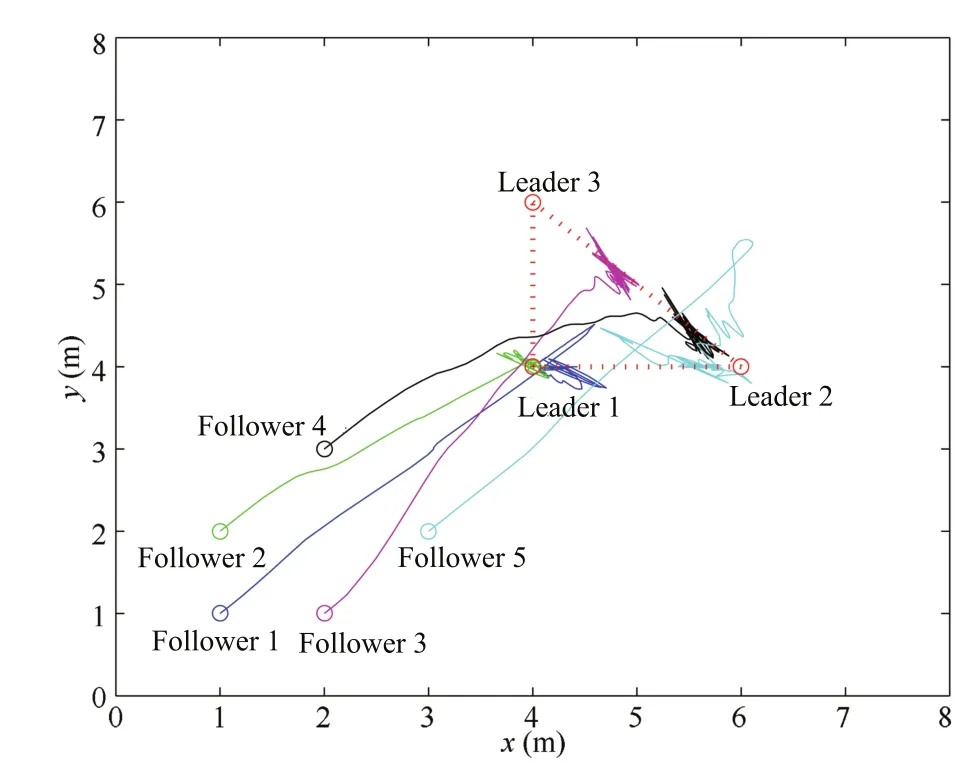
Fig.4.Moving track of FOMAS with communication delay τ=0.30.