Preparation of Hadamard Gate for Open Quantum Systems by the Lyapunov Control Method

Nourallah Ghaeminezhad and Shuang Cong,Senior Member,IEEE

Abstract—In this paper,the control laws based on the Lyapunov stability theorem are designed for a two-level open quantum system to prepare the Hadamard gate,which is an important basic gate for the quantum computers.First,the density matrix interested in quantum system is transferred to vector formation.Then,in order to obtain a controller with higher accuracy and faster convergence rate,a Lyapunov function based on the matrix logarithm function is designed.After that,a procedure for the controller design is derived based on the Lyapunov stability theorem.Finally,the numerical simulation experiments for an amplitude damping Markovian open quantum system are performed to prepare the desired quantum gate.The simulation results show that the preparation of Hadamard gate based on the proposed control laws can achieve the fidelity up to 0.9985 for the different coupling strengths.

I.INTRODUCTION

DURING recent years much work has been done to develop the quantum computers.In a quantum computer,the data is loaded as a string of quantum bits(qubits)[1].Quantum gates perform very simple operations on these qubits such as flipping their values.By combining many quantum gates,complex operations can be realized and these operations can be used to manipulate the qubits.The preparation of quantum basic gates is one of the most important research topics in quantum control field[2].The main objective is to prepare stable and high- fidelity quantum gates within a possible short time and prevent them from decoherence as long as possible[3].A quantum control process can be divided into coherent and decoherent parts,corresponding to the unitary and non-unitary operations,respectively[4],[5].Up to now,many different quantum control methods have been developed to generate higher fidelity quantum gates in a short time.One of the common methods is the quantum optimal control method,which has been extensively studied[6]−[11].Dynamical decoupling method is also an effective control way for the quantum gate preparation.In 2013,Piltz et al.protected conditional quantum gates by robust dynamical decoupling[12].In 2011,Grace et al.combined dynamical decoupling pulses with the optimal control method for improving preparation of quantum gates[13].However,in the methods mentioned above the control laws are not analytic and the designing procedure is a time-consuming task.The design of control laws based on the quantum Lyapunov method greatly simplifies the mathematic calculation and its analytical type of control laws make the control system be easily adjusted[14],[15].

The Hadamard gate is one of the most basic and important gates in quantum computers[16].Any unitary operation can be approximated with arbitrary accuracy by means of special gates set in which the Hadamard gate must be included.Many quantum algorithms use the Hadamard transformation as the first step to initialize the state with random information.In quantum information processing,the Hadamard transformation acts as a one-qubit operator that maps the qubit basis states to different superposition states[17].

In our previous work[18]we prepared a Not gate for one qubit open quantum system.In this paper,we will design a Lyapunov control method to prepare the Hadamard gate using unitary time-evolution operator whose dynamics are transferred to the Bloch vector space.We construct a matrix logarithm function as the Lyapunov function.The design of control laws is based on the Lyapunov stability theorem.The purpose of the control is to drive the unitary evolution operator from any initial quantum gate as close as possible to the desired quantum gate in the shortest possible time.Two performance indices of the system under environment uncertainties are analyzed by means of the simulation experiments.

The rest of this paper is arranged as follows:in Section II,the descriptions of the control system and the model of the system are studied.In Section III,the Lyapunov function and the design of control laws are investigated.In Section IV,the Hadamard gate based on designed control laws is prepared in numerical experiments,the performances of control laws are analysed,and the comparisons with other control methods are done.Finally,the conclusion is given in Section V.

II.DESCRIPTIONS OF THE CONTROL SYSTEM AND THE MODEL OF THESYSTEM

For a two-level Markovian open quantum system,the dynamics of state ρtcan be described as the following Lindblad equation[17]

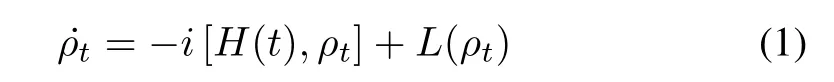
where[H(t),ρt]=[H(t)·ρt−ρt·H(t)]is the commutator of H(t)and ρt[19].H(t)is the Hamiltonian of the system

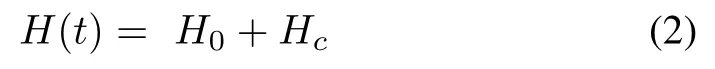
where H0is a free Hamiltonian which is a Hermitian diagonal matrix,and Hcis the control Hamiltonian of the system

where fx(t),fy(t)and fz(t)are control fields;σk,k=x,y,z are the Pauli matrices

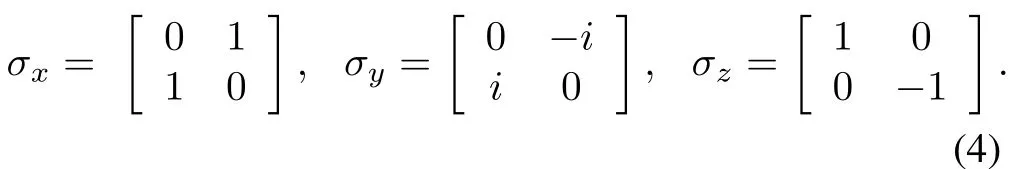
In(1),L(ρt)turns out to cause decoherence of the system and is called the dissipation part which describes the correlation between the system and the environment[17],[20],[21]

In our work,the studied model of the Markovian open quantum system is amplitude damping(AD).The related GKS matrix for the AD system is[22],[23]

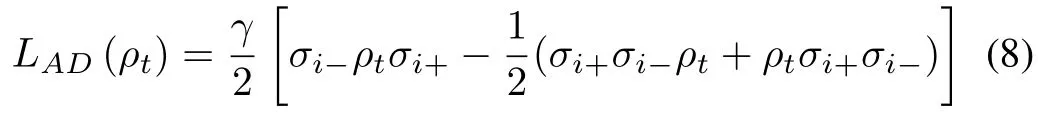
where σi−= σx−iσy,σi+= σx+iσy,and γ is the coupling strength of the system with the environment.

The preparation of quantum gates is more comprehensible if they can be considered as a kind of operators.Under this consideration,the dynamics of the operators must be obtained.Since the density matrix dynamics of(1)is a bilinear equation with dissipation part,it is not easy to use to manipulate the gates.Fortunately for a two-level quantum system,the state of the quantum system can also be described by the state vector.

As{I,σx,σy,σz}makes a basis for 2 × 2 Hermitian matrices,the density matrix ρtin(1)can be rewritten in Bloch vector rtas

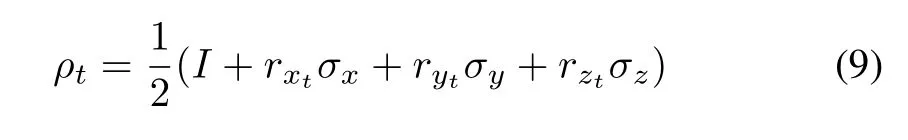
Moreover,the dissipation part of the AD system is[23]

in this way ρtis represented by the vector rt=(rxt,ryt,

We define U(t)as a unitary time-evolution operator on density matrix ρt;accordingly the time-evolution of ρtcan be written as

According to(1),(9)and(10),we can obtain the following dynamics equation

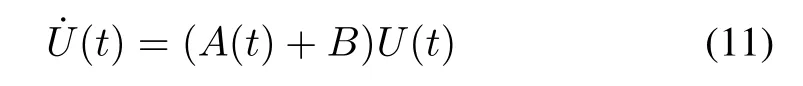
in which A(t)is the adjoint representation of−iH(t)in group of SO(3)which is derived from converting unitary part−i[H(t),ρt]of(1)to the Bloch vector representation and has the following form

where Ax=andB is extracted from converting the dissipation part L(ρt)of(1)to the Bloch vector representation and can be written as

Based on(6)and(7),for the AD system we set γxx= γyy= γ,γxy= γi,γyx= −γi and γxz= γyz= γzx= γzy=γzz=0.In this case,one has

From(9)and(10),the time-evolution of vector rtin the Bloch vector space can be written as

Accordingly,based on(11)we can obtain

Now for preparing the quantum gate,the control task becomes to design the control fields in A(t)in order to drive the initial gate towards the desired one.

By substituting the Pauli matrices(4)into the density matrix given by(9),the relationship between ρtand rtbecomes

where G†refers to the conjugate transpose of matrix G,and u∗stands for the conjugate of element u.

Let the final state vector be rf= (rxf,ryf,rzf)T,by comparing(17)with(18),rxf,ryfand rzfcan be obtained as

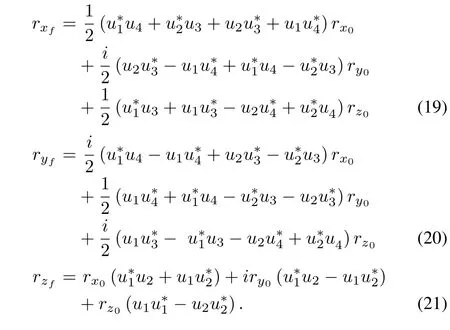
Considering(15),(19),(20),and(21),the time-evolution operator U(t),which drives the initial vector r0to the final vector rtin the Bloch vector space,can be derived as(22)(see the bottom of this page).

In this paper,the desired gate is a Hadamard gate GH,which is a unitary operator that implies on a single qubit,and transfers each basis stateto the superposition of both states,i.e.,it transfers the basis stateand the basis state The GHcan be written as[1]

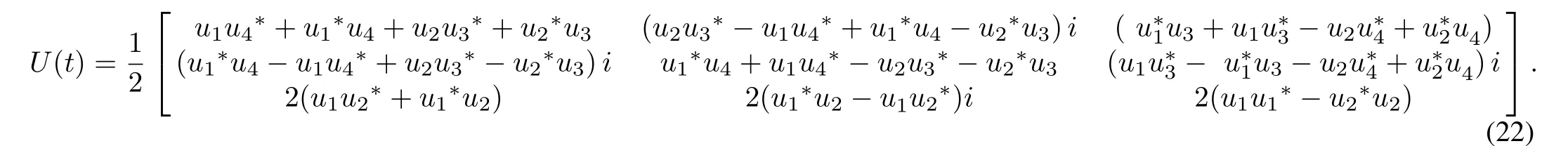
To obtain the Hadamard gate GHby the vector dynamics,the matrix GHwill be realized in the form of U(t)in(22)as the unitary time-evolution operator in the Bloch vector space.According toand(23),the final parameters of the Hadamard matrix in GH,i.e.,are substituted into(22);then the representation of the desired Hadamard gate in the Bloch vector space is expressed as

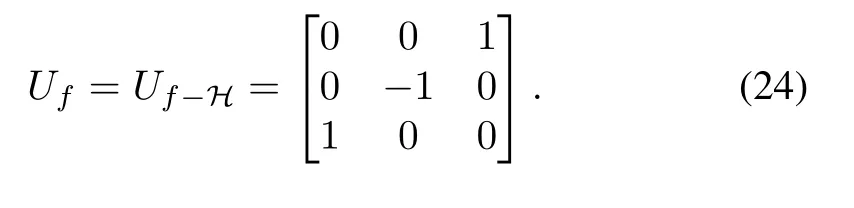
III.DESIGN OF CONTROL LAWS

In Section II,density matrix dynamics and desired quantum gate have been derived in the Bloch vector space,and we have obtained the dynamics of time-evolution operator U(t)in the same space.Now we design a proper Lyapunov function and Lyapunov-based control laws.A suitable Lyapunov function is first constructed and evaluated,then the control laws based on the Lyapunov stability theorem are designed.

The Lyapunov stability theorem is used to determine the stability of a control system without need of solving the partial differential equations.It can also be used to design the control laws in order to obtain a stable control system.According to the Lyapunov stability theorem the dynamical system in(11),is stable if there is a scalar function V(t)that satisfies the following conditions:a)V(t)is positive semi-definite,i.e.,V(t)≥0 at any time;b)the first order time derivative of the Lyapunov function is negative semi-definite,i.e.,˙V(t)≤0 at any amount of time[17].

The Lyapunov function V constructed in this paper is based on the matrix logarithm log(Uf†U(t))[25].Let’s define Uf†U(t)=W(t).As long as the spectral radius is less than one,the Mercator series of log(W(t))is[26]

where I is the identity matrix.

The first two terms of Mercator series in(25)are chosen,and the Lyapunov function in this paper is constructed by taking the square norm of two terms as

Equation(26)asserts that,V(t0)=32 when U(t)=U0=I,and V(tf)=0 as long as U(t)=Uf.The constructed Lyapunov function satisfies V(t)≥0 at any time.

To design the control laws,the first order time derivation of V(t)must satisfy˙V(t)≤0 at any amount of time,and˙V(t)=0 while U(t)=Uf.According to(26),˙V(t)is derived as follows:

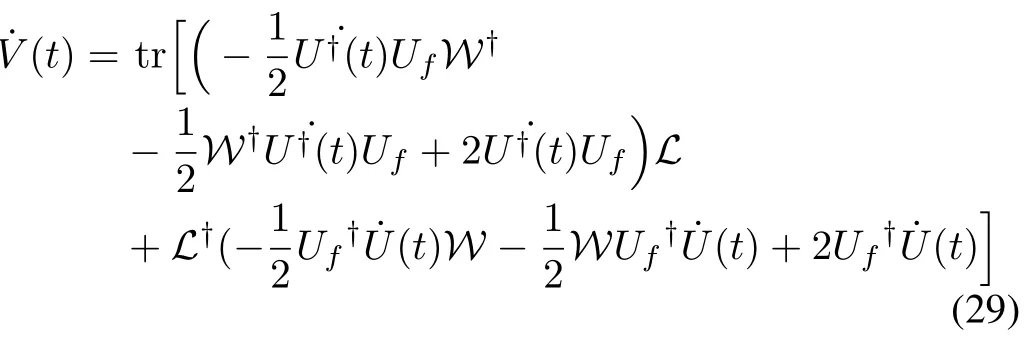
where the first and second terms of the trace function are the conjugate transpose of each other.Moreover,all elements of the trace function are real matrices,so the trace of these two terms are equal,and(29)can be rewritten as

Substituting the conjugate transpose of˙U(t)in(11),i.e.,˙U†(t)=U†(t)(A(t)+B)†into(30),one has

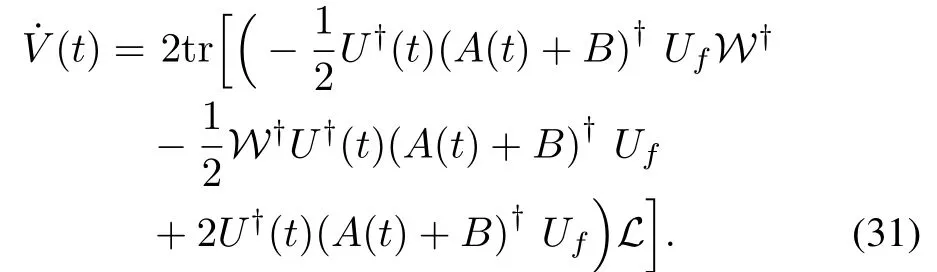
Substituting A(t)in(12)into(31),we can obtain

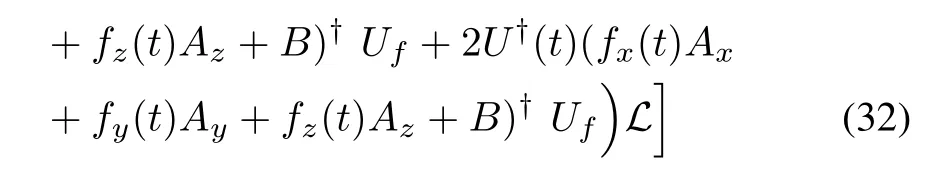
where B is defined in(14),and fx(t),fy(t),and fz(t)are real valued functions which are pulled out from the trace function to divide(32)into 4 parts as shown in(33)

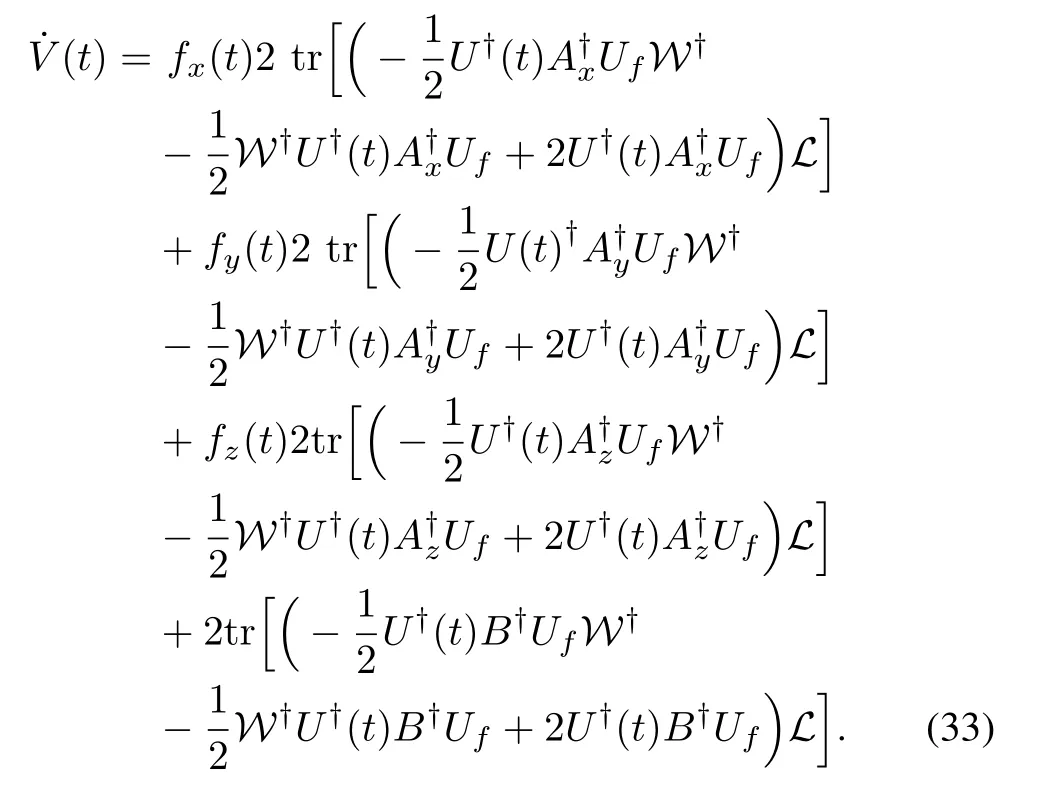
From(33)it is obvious that,˙V(t)is composed of 4 parts with the similar structure as

then these similar functions are defined as S(X,t)

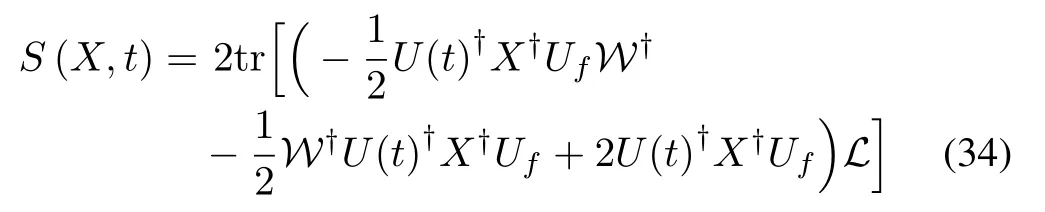
in which X is Ax,Ay,Azor B,in the first,second,third,or fourth term of(33)respectively.By substituting(34)into(33),we have

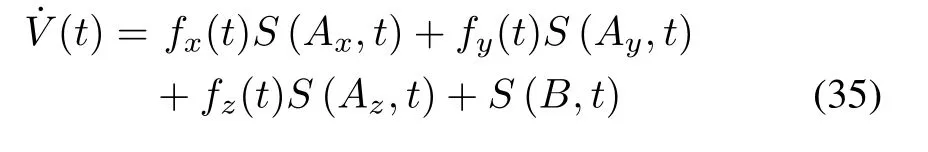
while Ax,Ay,Az,and B are defined in(12)and(14),respectively.

Now the control task becomes to design the control functions fx(t),fy(t)and fz(t),to make V(t)decrease monotonically,i.e.,˙V(t)≤0.The main idea of design is to make the control laws consist of two terms,such that the first term is used to ensure˙V(t)≤0,and the second term is used to eliminate the dissipation part caused by B.For this purpose,the control functions are designed as

where ax,ay,az,hx,hy,and hz,are tuning weights.In(36),the terms−ajS(Aj,t),aj≥ 0,j=x,y,z,are used for preparing the operator,while for terms−hjS(B,t)/S(Aj,t),j=x,y,z,by adjusting hj,hx+hy+hz=1,the dissipation part caused by B goes to be eliminated.

Substituting(36)into(35),one gets

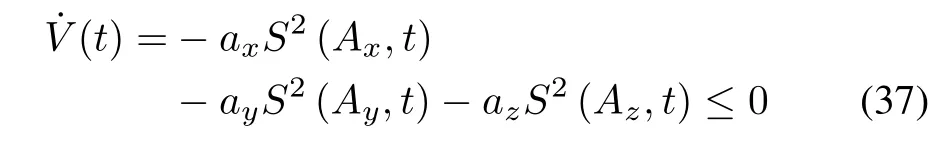
This means the control laws given by(36)can ensure≤0,so these control laws satisfy the requirements of the Lyapunov stability theorem.

IV.SIMULATION EXPERIMENTS AND RESULT ANALYSIS

In this section,the control laws in(36)are used to prepare the Hadamard gate for a Markovian open quantum system,i.e.,to drive the time-evolution operator U(t)from the initial identity matrix gate(38)to the desired gate(39).

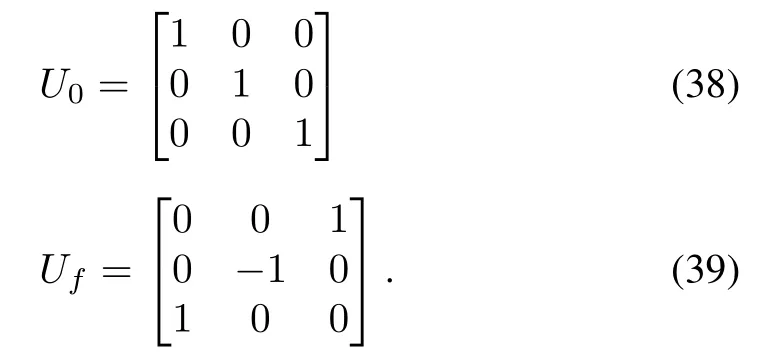
Numerical simulations are conducted to investigate the performances of control laws and the dynamical behavior of the system.We mainly study the following three points:

1)The dynamics and characteristics of the time-evolution operator under the Lyapunov-based control are investigated.Meanwhile,the accuracy of preparation of the Hadamard gate is analyzed based on two performance indices:the fidelity F and the distance D,for different coupling strength γ.Then,the performances of control laws are investigated by the experiments.

2)The effects of control laws on the control system performances are studied by analyzing the state-transfer from ρ0to ρf.

3)The comparisons between different control methods are discussed.

A.Preparation of Hadamard Gate and Analysis of the Control Performance Indices

In this subsection,the dynamics and characteristics of the time-evolution operator U(t)under the action of the control laws are studied.The Hadamard gate for the AD Markovian open quantum system is prepared,and two control performance indices are analyzed.

In dynamical equation˙U(t)=(A(t)+B)U(t),the four thorder Runge-Kutta method is used to obtain the time-evolution operator U(t)as

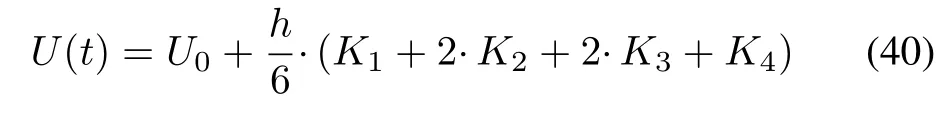
where

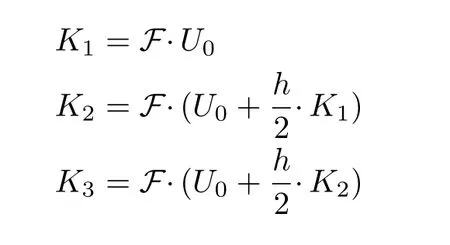
in which

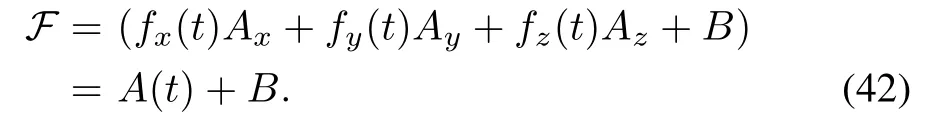
In(40),h is the sampling time.The control time is divided into 100 steps from 0 to 0.1a.u.,so h=0.001.As the steps go ahead,according to(40),the first step starts from U0,and the U(t)is updated until Ufis prepared.The control laws are used to drive U(t)from U0to Uf,in which ax=70,ay=106,and az=66 are set.At the initial time,we set the initial values of control functions as fx(0)=10.28,fy(0)=10.73,and fz(0)=40.

The fidelity and the distance are introduced to analyse the accuracy of quantum Hadamard gate preparation.The fidelity is defined as[27]

where N is the system dimensions and for the two-level system,N=2.As long as the operator reaches completely the desired operator,the fidelity is equal to one.

The distance is defined as

Accordingly,the distance gives the perception whether U(t)achieves Ufand to what extent.When U(t)reaches Ufcompletely,the distance is equal to 0.Otherwise by considering the fault tolerant quantum computation,the distance should satisfy the following performance selected in our experiment which is the distance criterion for valid operator preparations.

As the system is an open quantum system,when the coupling strength γ increases,there is a higher coupling strength with the environment.Fig.1 shows the experimental results of the fidelity,when preparing the Hadamard gate for the AD Markovian open quantum system under designed control laws with three coupling strength γ = 0.01, γ = 0.1,and γ = 0.18,respectively.

Fig.1.The fidelity under control laws for the AD system when γ=0.01,γ=0.1,and γ=0.18.

One can see from Fig.1 that,when γ=0.01,at t=0.0164a.u.,the fidelity reaches 0.9985.For larger parameters γ,i.e., γ =0.1 and γ =0.18,the fidelity becomes 0.981 and 0.962,respectively.This indicates that as γ increases,the dissipation part has more effect on the system,which makes the fidelity decrease.When γ=0.1 at time 0.091a.u.,the fidelity has a fluctuation,and when γ=0.18,the fluctuations happen again with larger deviation at times 0.0447a.u.and 0.092a.u.,which are caused by the dissipation L(ρt)of the open quantum system.The designed Lyapunov control laws can guarantee the system stability,and when the dissipation makes the system deviate from the desired result,the control laws can eliminate it in a very short time.

Fig.2 is the result of the distance when preparing the Hadamard gate for the AD Markovian open quantum system with γ =0.01, γ =0.1,and γ =0.18.For all parameters γ,at t=0.0164a.u.,the distance reaches less than 10−4,and it remains in this criterion for the rest of time.For γ=0.1,at t=0.092a.u.,the distance becomes 4× 10−3,but after a short time the controller brings it under 10−4again.When γ=0.18,at times 0.047 and 0.093a.u.,there are also some peaks that values are 3.1× 10−2and 5 ×10−3,respectively,but these fluctuations are rectified by the controller.These fluctuations are caused by the dissipation of the system coupled to environments.As the γ increases the fluctuations also increase,which are eliminated by the control laws in a very short time.

The function of control laws consists of two parts:the first is the preparation,and the second is the preservation.During the preparation part,the desired gate is prepared,and two control performance in dices,i.e.,density and fidelity,tend to reach the minimum and maximum values,respectively.In the preservation part,the desired gate remains stable under the action of the control laws.The effects of control laws in the preservation part eliminate the dissipation of the system which emerges as the fluctuations.

Table I is the parameters in(36)selected in experiments in order to have the maximum fidelity and the minimum distance in the shortest possible time.The control laws as the function of time with γ=0.1 are shown in Fig.3.From which one can see that at t=0.0164a.u.the control laws tend to zero,then there appear some fluctuations.This time is the preparation time and during 0≤t≤0.0164a.u.,the control laws work in the preparation part.After t=0.016a.u.and till the end of simulation time t=0.1a.u.,the control laws work in the preservation part.

B.State-Transfer Under Designed Control Laws

In this subsection,in order to study the relation between the density matrix and the gate,the numerical simulation of corresponding state-transfer from the arbitrary identity matrix U0to desired gate Ufis fulfilled to verify the effect of designed control laws.From(15)and(17),one can see that the density

Fig.2.The distance under control laws for the AD system when(a)γ=0.01,(b)γ=0.1,and(c)γ=0.18.

matrix ρtis an implicit function of U(t)by means of vector rt.

Let the initial vector be r0=(1,0,0),which is regarded to be the superposition of basis states,i.e.,According to(15)and(24),the desired final vector,which is correlated to the state■■0〉,can be derived as

TABLE IMINIMUM VALUES OF D AND MAXIMUM VALUES OFF

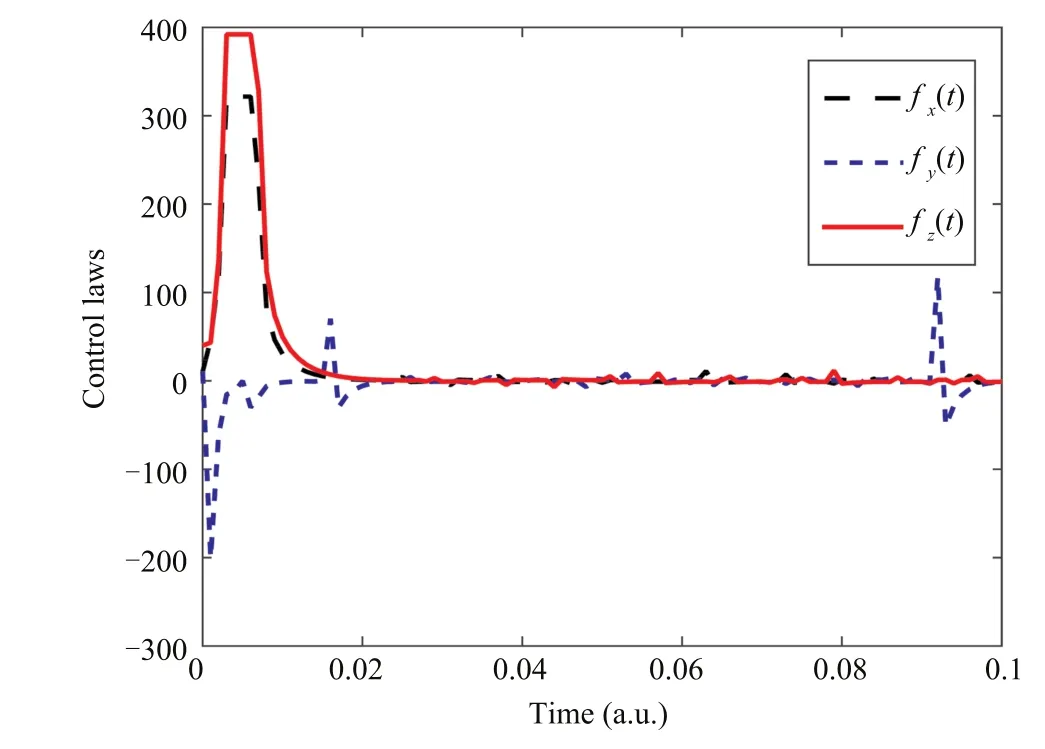
Fig.3.Control laws as the function of the time when γ=0.1.

To find out the corresponding density matrix,the initial vector r0=(1,0,0)and the final desired vector rf=(0,0,1)are substituted into(17),we can obtain

Fig.4 illustrates the trajectory of the time-evolution density matrix as a function of time for the AD Markovian open quantum system under the designed control laws.

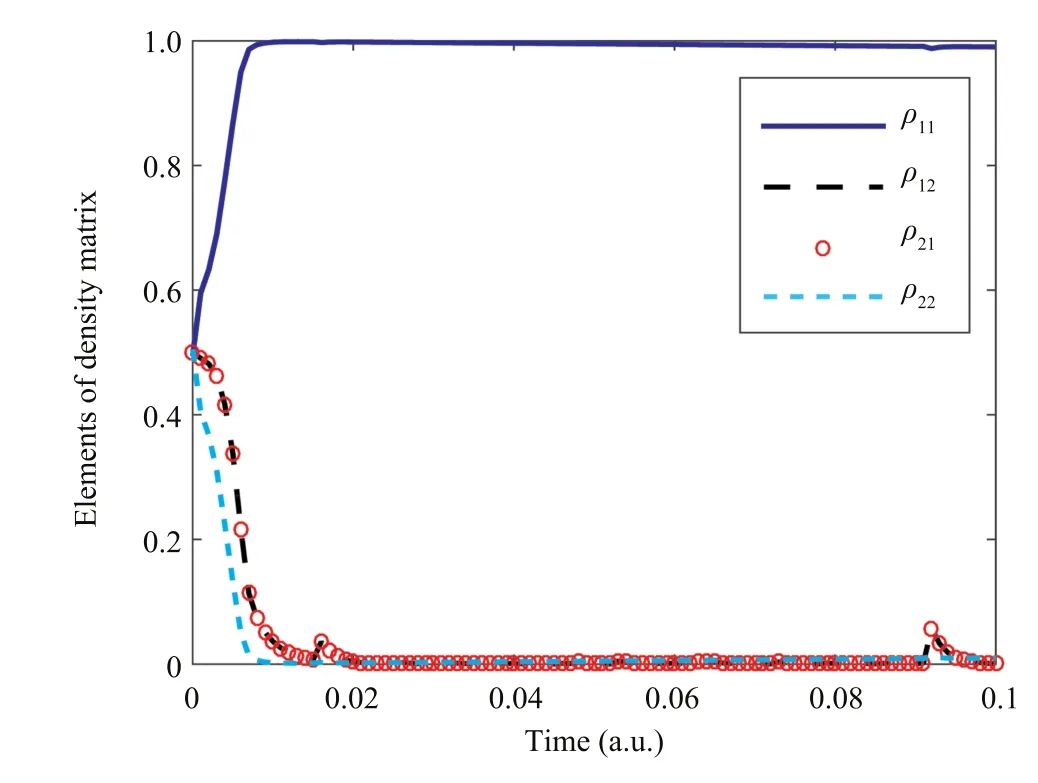
Fig.4. State-transfer from ρ0to ρfunder control laws for the AD system when γ=0.1.

Based on the principle of Von Neumann,the diagonal elements of a density matrix can be interpreted as the probability.The trace of a density matrix must be normalized,which means the sum of the diagonal elements of time-evolution density matrix,i.e.,ρ11+ ρ22,must be equal to one at each moment of time-evolution[28].The numerical simulation results in Fig.4 show that,at t=0.012a.u., ρ11and ρ22attain 0.999 and 0.001,respectively,whose sum is one.For the rest of simulation time,the loss of stability in Hamiltonian makes ρ11decrease and fluctuate very little away from the desired amount.Under the action of control laws,ρ11remains stable close to 1[29].When ρ11decreases a bit,the other diagonal element,i.e.,ρ22slightly increases,in which the sum of ρ11and ρ22is always equal to one.Other elements,i.e.,ρ12and ρ21attain to 4 × 10−4at t=0.012a.u..From Fig.4 one can see that,at times t=0.015a.u.and t=0.091a.u.,there are some fluctuations in the trajectories of ρ12and ρ21,which can be eliminated by the control laws designed.The numerical simulation results verify that the desired state in(47)is achieved.

C.Comparison and Discussion

In[30],the optimal control theory is applied to a two level open quantum system to prepare the Hadamard gate by minimizing an energy-type cost functional.25a.u.time was used and the performance of F ≈ 1−10−16was achieved for a closed-loop system.In our paper,when the experimental simulations are done in the same conditions,i.e.,γ=0,and the maximum amplitude of control laws is no larger than 2,the performance of our experimental results is F =1 at t=2.025a.u.which indicates that the control method proposed in this paper can obtain higher fidelity in a shorter time compared to that of the optimal control method in[30].

In[18],the Lyapunov control method is used to prepare a Not gate for a two-level open quantum system.The performance of F=0.9976 at t=0.0194a.u.is obtained with γ=0.01,and the maximum amplitude of control laws is less than 400.Under the same conditions the fidelity performance in our paper is F=0.9985 at t=0.0165a.u.,which demonstrates the preparation in this paper has higher fidelity with a faster convergence rate.

V.CONCLUSION

This paper has prepared a Hadamard gate for the two level AD Markovian open quantum system based on the Lyapunov stability theorem.The controlled system dynamics are obtained in the Bloch vector representation.Two control performance indices,i.e,the fidelity and the distance are investigated,and numerical simulations are implemented under the MATLAB environment with different coupling strength γ.The control laws which are designed based on a novel Lyapunov function ensure high fidelity and low distance with a very short preparation time.The performances of the gate preparation and the state-transferring illustrate the effectiveness of designed control laws to eliminate the dissipation caused by coupling with environment.