频差偏差对全视场外差测量精度的影响∗

伍洲张文喜 相里斌李杨1孔新新

1)(中国科学院计算光学成像技术重点实验室,北京 100094)

2)(中国科学院大学,北京 100049)

1 引 言

激光外差干涉测量具有高精度、高环境适应性等优点.由于激光外差的频率较高,难以采用面阵探测器进行探测,从而导致长期以来外差测量仅用于距离、角度等点探测领域[1−4].随着电子技术的发展,赫兹级频差的移频技术的出现,使外差技术可用于三维形貌[5−8]、光滑表面[9]、数字全息和散斑等[10−16]测量领域,极大地提高了面形测量的精度和稳定性.

外差干涉的频差通常由声光移频器实现.为了保证移频的效率,声光移频器的驱动频率一般大于20 MHz.低差频声光移频器是通过两路频差在赫兹级的同相射频信号驱动控制实现的.采用高稳定度参考信号作为两路同相输入,如恒温晶体振荡器,利用数字鉴相器对压控振荡器进行锁相,结合小数分频回路,使压控振荡器的输出频率与所需控制信号的频率完全一致,通过不断的鉴相-锁相反馈,从而得到精确而稳定的输出频率.环境温度的变化、供电电源的稳定性、振荡器的负载变化及使用时间等因素,均会引起振荡器标称频率的变化,直接影响输出频率的准确度和稳定度.因此低频差移频器的频差真实值与设计值具有一定的偏差,这个偏差称为频差偏差.频差偏差会导致外差频率与面阵探测器的探测频率无法严格匹配,影响了测量精度的提高.本文基于全视场外差测量和解调理论,详细推导了外差频率偏差与初始相位、外差频率、采样频率和采样周期的相互关系,分析了频率偏差对提高测量精度的主要影响因素,为全视场外差测量系统参数的选取提供依据.

2 频差偏差与测量精度的关系

全视场外差测量采用双移频器,图1为外差泰曼格林型全视场干涉仪原理图.激光经分光棱镜分成两束,两束激光分别经过两个声光移频器,两路固定频差的射频驱动信号加载在声光移频器上,保证了外差频率的稳定性.

移频后的两束激光分别经参考面和测量目标表面返回到面阵探测器,探测其外差干涉条纹并经数字解调能够反演获得目标表面信息.其外差干涉表达式为[17−19]

图1 泰曼格林型全视场外差干涉仪Fig.1.Twyman-Green full- fi eld heterodyne interferometer.

其中fH,φO,φR,aO,aR,t分别为外差频率的真实值、目标波的初始相位、参考波的初始相位、目标波的振幅、参考波的振幅和采样时间.用采样频率为fS的探测器采集N组数据,对采集的数据进行数字解调[20,21]:

其中fM为解调频率,fM的值为频率偏差的设计值.当采样频率fS=NfM,且N≥2时,

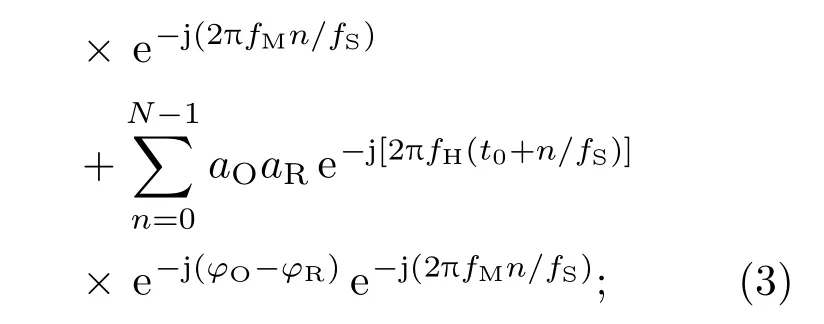
当外差频率fH=fM时,

全视场外差直接测量值为视场内任意空间点1,2的相位差φ12:

由(5)式可得,当外差频率等于解调频率,即频差没有偏差时,采样初始时间、采样频率和采样点数等参数不影响测量结果.由于需要保证采样频率fS是解调频率fM的整数倍,而采样频率为面阵探测器的帧频,面阵探测器的帧频难以任意设置.因此如果外差频率存在小的偏差,很难保证解调频率等于外差频率,即fH/=fM时,

其中,

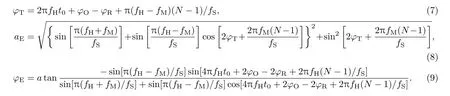
当外差频率与解调频率不一致时,通过(6)式得到的相位信息由φT和φE两部分组成.空间点1,2的相对相位如下式:

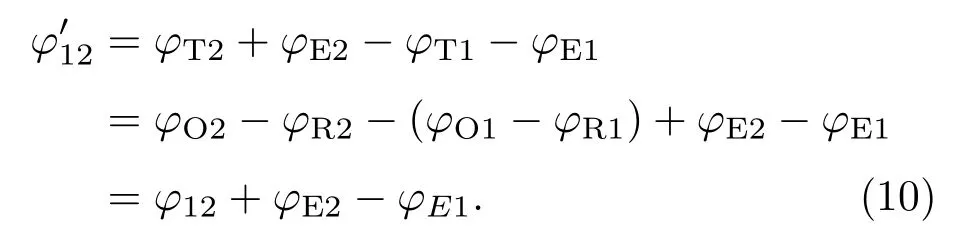
因此在全视场外差测量中,当频率频差存在时会对测量的精度造成影响,频差偏差fH−fM造成的测量误差来源于φE.根据(9)式,t0,φO−φR,fM,fS和N等参数会对测量精度有一定的影响.

3 频差偏差对测量精度的影响分析

3.1 初始时间、相位对测量精度的影响

图2 外差干涉不同测量时刻的干涉图和相位图 (a)t1时刻干涉图;(b)t1时刻相位图;(c)t2时刻的干涉图;(d)t2时刻的相位图Fig.2.Interferogram and phase diagram at different measurement moments:(a)Interferogram at t1;(b)phase diagram at t1;(c)interferogram at t2;(d)phase diagram at t2.

全视场外差干涉测量不同初始时刻测量的干涉图不同,解调获得的初始相位也不同.图2为待测面为球面、参考面为平面时全视场外差干涉测量的两次仿真结果.从图中可以看出,尽管两次测量任意两点的相位差相同,但两次测量的初始相位不同.根据(9)式可知不同的初始相位2πfHt0+φO−φR导致的误差不同,且具有周期性分布,周期为π.初始相位为图2(b)的探测数据的误差分布如图3所示,其探测器帧频为20 Hz、解调频率为5 Hz、采样帧数为4帧.

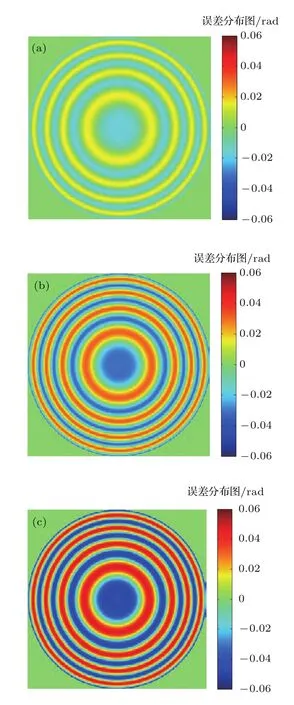
图3 初始相位对测量精度的影响 (a)频差偏差0.1 Hz;(b)频差偏差0.2 Hz;(c)频差偏差0.3 HzFig.3.Effect of initial phase on measurement accuracy:(a)Frequency difference deviation is 0.1 Hz;(b)frequency difference deviation is 0.2 Hz;(c)frequency difference deviation is 0.3 Hz.

从图3仿真结果可以看出,当外差频率具有偏差时,初始相位对全视场外差测量的测量精度具有一定的影响,误差分布与初始相位的分布相同.此外,频差偏差的大小对测量精度也有较大的影响,频差偏差越小,测量精度越高.图4给出了不同频差偏差下初始时刻、相位对测量精度影响的仿真结果.其中探测器帧频20 Hz、解调频率5 Hz、测量采样帧数为5帧.前4帧处理的误差如图4(a)所示,横坐标为频差相对于5 Hz的偏差,纵坐标为初始相位−π/2—π/2.图4(b)为后4帧相位误差,对应点的误差大小与图4(a)对应点的误差大小基本相同,但其符号相反,通过这两次测量取均值能够有效提高测量精度.图4(c)为两次测量联合处理后的误差,可以看出其误差最大值减小1/30以上.因此,选择合理测量方案和处理方式能够有效提升全视场外差的测量精度.

图4 初始时间、相位、频差偏差对测量精度的影响 (a)t=0时的误差分布;(b)t=0.05 s时的误差分布;(c)两次测量联合处理误差分布Fig.4.Effect of initial time,phase and frequency difference deviation on measurement accuracy:(a)t=0 error distribution;(b)t=0.05 s error distribution;(c)joint processingerror distribution of two measurements.

3.2 频差大小对测量精度的影响

全视场外差测量使用的低频差声光移频器,其比较成熟的产品最低频差为3 Hz.频差越小其频差的稳定性越差,测量精度会下降.但频差越高要求面阵探测器帧频越高,探测器选择范围越小,系统的成本也越高.干涉测量中测量误差的峰值(PV)是衡量系统能力的主要指标.图5给出了3,5和10 Hz三种频差下不同频差偏差与误差相互关系的仿真结果.其中采样帧频分别为12,20和40 Hz,采样帧数均为4帧.可以看出测量误差的PV值与频差偏差基本成正比,频差偏差越大,测量精度越低.相同频差偏差情况下,频差越大,测量精度越高.因此,在选择声光移频器驱动时要根据系统的指标要求、造价等综合判断,选择合适的频差和频差偏差指标,以减小声光移频器驱动的开发难度和系统造价.

图5 频差大小及偏差对测量精度的影响Fig.5.Effect of frequency difference and deviation on measurement accuracy.

3.3 采样频率、采样周期数对测量精度的影响

在干涉测量过程中,外界振动、光源功率稳定性、探测电路噪声等因素对测量精度有着较大的影响.为了有效抑制外界噪声,全视场外差技术通常通过增加采样频率和采样周期抑制噪声对测量精度的影响.根据(9)式,改变采样频率和采样周期即改变N值,频差偏差导致的误差同样会变化.图6为解调频率5 Hz,差频偏差分别为0.05,0.04和0.03 Hz情况下,全视场误差的峰值与单周期内采样点数的关系.可以看出频差偏差越大,误差的PV值越大.在频差偏差一定的情况下,单周期内增加采样帧数能减小PV值,提高测量精度.当单周期采样帧数大于15时,误差PV值趋于平缓,增加采样帧频对提高测量精度意义不大.

图6 测量精度与采样频率的关系Fig.6.Relationship between measurement accuracy and sampling frequency.

图7给出了采样周期数与误差PV值的关系,其中解调频率5 Hz,差频偏差为0.05 Hz.采用多周期数据对频差偏差引起的测量误差没有影响.即可以通过采集多周期的数据,抑制其他噪声对测量精度的影响,提高仪器的测量精度.

图7 测量精度与采样周期数的关系Fig.7.Relationship between measurement accuracy and sampling cycles.

4 结 论

研究了低频差移频器的频差偏差对全视场外差测量精度的影响,并推导了影响公式.当频差偏差已知时,可以通过该公式校正测量误差,当频差偏差难以测量或测量精度不足时,可以通过该公式对仪器的性能进行初步判断.

仿真分析了当频差存在偏差时,初始采样时间、初始相位、频差、频差偏差、采样频率和采样周期数对测量精度的影响,通过上述分析可以得出如下结论.

1)初始采样时间和初始相位对测量精度的影响相同,即测量精度与相位具有固定关系,具有周期性,其周期为π.通过合理选择测量参数和处理方法,能够大幅提高仪器的测量精度.

2)全视场外差测量误差的PV值与频差偏差具有线性关系,频差偏差越大,误差PV值越大.在频差偏差一定的情况下,频差越大,测量精度越高,但是对探测器帧频的要求越高.在进行仪器设计时要综合考虑,选择合适的频差参数.

3)在频差偏差一定的情况下,增大采样频率能够提高测量精度,单周期内采样帧数达到15帧后测量精度的提升有限.多周期采样对频差偏差导致的测量误差没有影响.该误差为仪器能达到测量精度的极限值,可以作为全视场外差测量设备测量精度分析的理论依据.

[1]Wu G,Takahashi M,Arai K,Inaba H,Minoshima K 2013Sci.Rep.3 1894

[2]Torre R,Taschin A,Sampoli M 2001Phys.Rev.E64 061504

[3]Wang G C,Yan S H,Yang J,Lin C B,Yang D X,Zou P F 2013Acta Phys.Sin.62 070601(in Chinese)[王国超,颜树华,杨俊,林存宝,杨东兴,邹鹏飞 2013物理学报62 070601]

[4]Yuichi K,Daisuke,Tomohiro K,Toyohiko Y 2010Opt.Lett.35 101548

[5]Tomasz T,Romuald J 2001Proc.SPIE4190 123

[6]Kong X X,Xiang L B,Zhang W X,Wu Z,Li Y,Lü X Y 2017Proc.SPIE10329 103292E-2

[7]Mark C P,Chung W S,Michael G S 2004Opt.Lett.29 111200

[8]Patrick E,Michael J C,Fereydoun L,Maurice P W 2006Opt.Lett.31 070912

[9]Wu Z,Zhang W X,Xiang L B,Kong X X 2017Proc.SPIE10329 1032905

[10]Clerc F L,Collot L,Gross M 2000Opt.Lett.25 100716

[11]Gross M,Goy P,Forget B C,Atlan M,Ramaz F,Boccara A C,Dunn A K 2005Opt.Lett.30 111357

[12]Atlan M,Gross M 2007Opt.Lett.32 111456

[13]Michel G 2016Appl.Opt.55 0300A8

[14]Michel G 2017Appl.Opt.56 071846

[15]Dario D,Alexey B,Daniel A,Michel G 2016Opt.Express24 26887

[16]Mauro V A,Fereydoun L,Maurice P W,Michael J C 2007Optics and Lasers in Engineering45 677

[17]Liao L,Yi W M,Yang Z H,Wu G H 2016Acta Phys.Sin.65 140601(in Chinese)[廖磊,易旺民,杨再华,吴冠豪2016物理学报65 140601]

[18]Li C Q,Wang T F,Zhang H Y,Xie J J,Liu L S,Guo J 2016Acta Phys.Sin.65 084206(in Chinese)[李成强,王挺峰,张合勇,谢京江,刘立生,郭劲 2016物理学报 65 084206]

[19]He Y Z,Zhao S J,Wei H Y,Li Y 2016Acta Phys.Sin.65 084206(in Chinese)[贺寅竹,赵世杰,尉昊赟,李岩2016物理学报65 084206]

[20]Holmes R B,Ma S,Bhowmik A,Greninger C 1996J.Opt.Soc.Am.A13 351

[21]Zhang W X,Xiang L B,Kong X X,Li Y,Wu Z,Zhou Z S 2013Acta Phys.Sin.62 164203(in Chinese)[张文喜,相里斌,孔新新,李杨,伍洲,周志盛2013物理学报62 164203]