用于热光伏系统的近场辐射光谱控制表面结构∗
2018-08-10于海童刘东杨震段远源
于海童 刘东 杨震 段远源
1)(清华大学,热科学与动力工程教育部重点实验室,二氧化碳资源化利用与减排技术北京市重点实验室,北京 100084)
2)(南京理工大学能源与动力工程学院,南京 210094)
1 引 言
热光伏(TPV)发电系统是一种新型能源转换系统,核心部分为热发射器和热光伏电池两部分,工作时,半导体电池通过光伏效应将高温发射器的辐射电磁波转化为电子空穴对,完成热能到电能的转换过程[1,2].热光伏系统能量来源多样,无运动部件,运行安静稳定;与直接光伏转换相比,热光伏的工作时间不受昼间阳光照射时段所限,且由于热源的辐射光谱可进行人为调控,因此可以设计窄带热辐射源代替宽谱带太阳能辐射,使能量转换效率打破单能带太阳能光伏的肖克利-奎伊瑟极限(S-Q极限)[3].热光伏系统的输出功率受热发射器辐射功率制约,而发射器温度受材料耐热性限制不能无限升高,因此为提升输出功率,提出了近场热光伏系统的思路,热发射器与电池仅由亚微米量级真空间隙隔开,此时辐射电磁波的倏逝分量可通过隧穿效应通过间隙,承载由发射器到电池的能量传递,即近场辐射效应[4].通过利用倏逝波,近场辐射热流能够远远超过远场辐射的黑体上限,实验也证明了将发射器与吸收器的真空间隙缩减到2µm以下时,热光伏系统的电流出现跃升[5],验证了近场热光伏系统的可行性.
为实现高效率的热光伏能量转化,需要有效操控系统中的辐射热流光谱分布,这是由于被电池吸收的辐射电磁波中能量低于电池能带的长波辐射无法转化为光生电流,而能量过高的短波部分在激发电子-空穴对后还有剩余能量,两种情况都直接导致能量转换效率下降,并会产生热量使电池性能恶化,因此热光伏系统的设计与常规光伏系统一样,都希望尽可能增强波长略短于电池能带的热流,而抑制其他波段的辐射传热.远场光伏系统常在半导体电池表面添加减反射薄膜或陷光微结构以增加吸收率[6],但现有设计难以直接应用于近场热光伏系统,原因如下:1)添加的表面结构或涂层可能与近场间距尺度接近,显著改变发射器与吸收器间的等效间距和辐射传递机理;2)近场辐射传热多由倏逝波主导,而远场减反射设计中未考虑倏逝分量,直接应用于近场会产生新的问题.实验和理论均已揭示远场增益辐射传热结构在近场间距下可能失去增强效果甚至削弱近场辐射传热,反之亦然[7,8].此外,热光伏系统常用的III-V族半导体电池在能带附近折射率高,吸收辐射电磁波能力差,增加了热光伏系统提升功率和效率的难度[9].
寻找和设计适用于近场热光伏应用的材料和结构,需要高效、严谨的近场辐射传热计算方法,不能简单套用远场的辐射和光学设计流程,一是因为基于黑体辐射定义的热发射率在近场辐射传热中失去了意义,二是因为近场热辐射可以激发平面内任意波数切向分量的行波或倏逝波模式,而基于远场光学响应的计算方法只能考虑行波部分[10].近场辐射传热的直接计算需要以涨落耗散理论为基础给出热辐射的源项分布规律,再由系统的格林函数给出辐射电磁波的分布[11].对于一维多层结构,格林函数的形式可以被简化,得到近场辐射热流的解析解[12].对于更复杂结构参与的情况,目前研究多使用等效介质理论(EMT)[13−15]将非均匀结构通过等效法则近似为具有等效介电常数的均匀层,再使用一维结构解析解.Vongsoasup等[16]设计用钨的矩形光栅作为热发射器,利用EMT计算发现发射器具有双曲超颖材料特性,相比无结构钨发射器获得了更高的热流,但该设计使不能被利用的长波热流被同时增强,能源转换效率未能有效提高.Chang等[17]采用EMT计算了钨纳米线到InGaSb电池的近场传热,并使用薄膜电池,由电池的全内反射控制了无用的长波热流,同时显著提升了系统的热流峰值与能源转化效率.但事实上EMT对近场辐射的应用范围并没有定论[18],原因在于近场辐射中倏逝波的参与,且传热路径尺度与结构尺度可能处于同一量级.此外也有研究证明对于金属性组元,即使结构特征尺度远小于特征波长,使用EMT仍可能与精确解偏差较大[19].
目前能够严格表征复杂结构参与的近场辐射热流的计算方法,一般是将涨落耗散理论与Maxwell方程的解相结合,改写已有的电磁学计算方法以适用于近场辐射计算,使用的方法包括时域有限差分(FDTD)法[10,20]、傅里叶模态法(FMM,又称严格耦合波分析)[21]、有限元法(FEM)等[22].其中,FDTD方法通过模拟系统对电磁波的时间域响应,通过傅里叶变换得到频域响应规律,一次模拟即可获得全光谱特性,编程简单,适用于任何形状的系统,且时域模拟易于表征近场辐射中常涉及的表面波传递等物理现象,是一种效率高、普适性强的近场辐射传热计算方法.
本文借助基于涨落耗散理论的FDTD近场辐射模拟方法,设计并验证了一种用于近场热光伏系统的辐射传热光谱控制表面结构,即III-V族电池表面的二维光栅结构.计算结果显示带表面光栅的GaSb电池与支持近红外表面波传播的发射器结合,可获得电池能带波长以下窄波段的选择性高近场辐射热流,峰值可达使用同温度远场黑体发射器时的2—3倍.使用FDTD方法模拟了系统的频域和时域响应特性,揭示了一种新的近场辐射光谱控制机理,即表面栅格结构与发射器表面波的近场耦合,由此满足高效率、高功率热光伏系统的辐射传热设计要求.
2 模 型
2.1 物质与结构
热光伏系统的辐射换热组件包括电池与热发射器两部分.受热发射器耐高温能力限制,一般设计辐射热流峰值和电池能带在近红外波段匹配以实现高功率与高转换效率.电池通常选择低能带III-V族半导体,以最常用的GaSb为例,其能带为0.726 eV,对应电磁波波长λ=1.7µm、频率ω=1.1×1015rad/s.热发射器方面,为激发窄波段内的高近场辐射热流,可以使用支持表面等离子体激元(SPP)、表面声子激元(SPhP)等表面波传播的材料,但自然界中不存在支持近红外表面波的材料,而能调制表面波频率的纳米结构难以满足热发射器的高温热稳定性需求.因此本文设计采用人工合成半导体——掺杂氧化锌作为热发射器,其SPP频率位于近红外区间,不需要附加表面结构即可激发SPP,且可通过掺杂组分类型与质量分数调制SPP频率.考虑采用GaSb电池,故选择掺杂比例为6%的ZnO:Ga(GZO),其SPP频率(ωSPP=1.39×1015rad/s)恰好略高于电池能带,以有选择性地增加电池能带之上的近场辐射热流.图1对比了几种材料的近场辐射光谱热流,使用GZO作为发射器获得的辐射热流比传统耐高温金属(W,Mo,Ta等)更高,但与GZO同种材料间的辐射换热相比,GZO到GaSb的辐射热流峰值明显较低,原因是GaSb在红外波段的折射系数高(n≈4),导致其菲涅耳反射系数高,不能吸收GZO发射器的SPP窄带辐射,光谱选择性潜力没有得到充分利用.
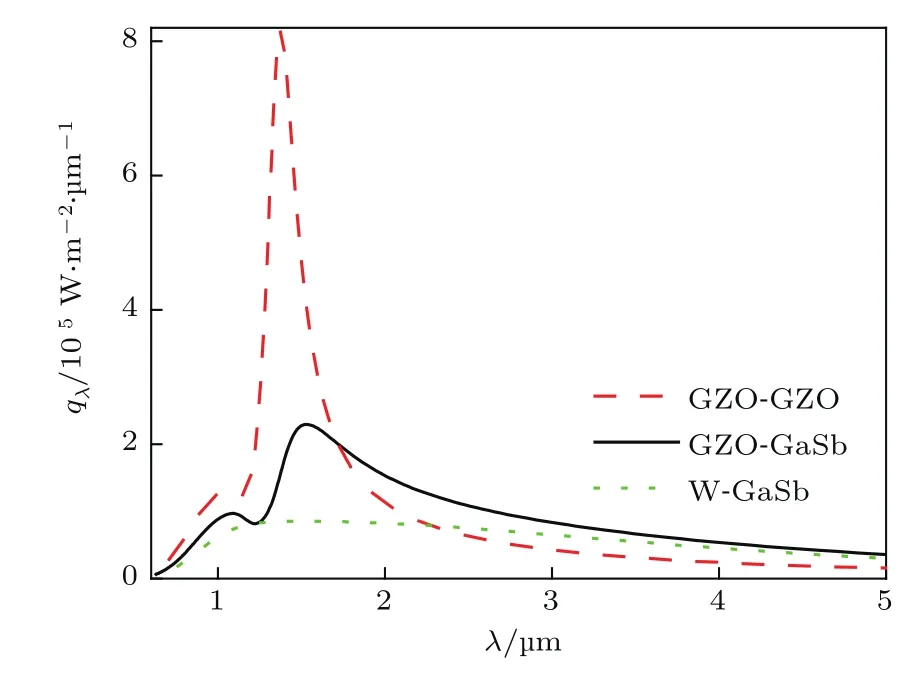
图1 平行平面材料间的辐射光谱热流qλ解析解(近场间距d=200 nm,两侧材料温度为1800和300 K)Fig.1.Analytical solution of spectral radiative fl ux between bulk materials(1800 K to 300 K)separated by a gap of 200 nm.

图2 计算模型示意图 (a)物质、结构及尺寸参数定义;(b)数值计算域示意图Fig.2. Illustration ofthecomputation model:(a)Materials,surface structures,and de fi nition of parameters;(b)numerical calculation domain.
为此,进一步设计对GaSb端进行改性以提升其近场辐射吸收能力.比拟远场光伏系统中的减反射表面,在GaSb表面添加二维正方形栅格结构(图2(a)),形状由周期长度Λ、柱面边长a与柱面高度h三个尺寸参数完全确定,相应地有光栅填充比例f=(a/Λ)2,槽宽w=Λ−a.已证明具有高尺寸比例的光栅、纳米线等表面结构在远场辐射问题中能有效增加III-V族半导体的吸收率[23],但对近场辐射传热的作用尚不清楚.此外,辐射传热计算中一般不需要针对异质结独立建模,因为其光学特性与GaSb基体基本一致,对辐射传热计算的影响可以忽略[24].本文计算中除非另加说明,否则均假定近场间距d=200 nm,发射器温度为1800 K,GaSb电池温度为300 K.
2.2 模拟方法
使用FDTD方法计算GZO与带表面结构GaSb间的辐射传热,模拟域如图2(b)所示.普通FDTD方法计算发射率和吸收率时,一般使用远场入射平面波作为源项研究系统的响应特性,该方法显然无法直接模拟近场辐射传热.根据涨落耗散定律给出的热辐射能量源项形式,在物体内部填充电流源项J,其分布规律服从[20,25,26]:
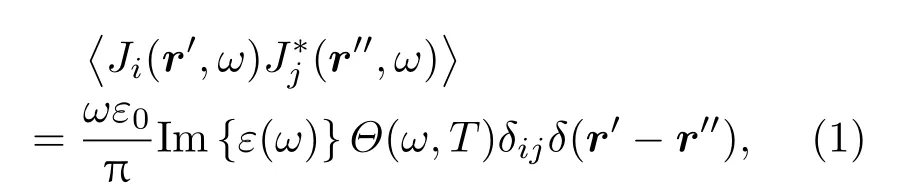
式中〈〉代表取统计平均值,∗为取共轭,Im{}为取虚部;r为空间坐标矢量,i,j=x,y,z代表各坐标分量;δ为Kronecker符号,反映任意不同位置以及任意不同坐标分量电流源项的不相干性;ω为电磁波角频率,ε(ω)为物质介电常数,ε0为真空介电常数;Θ= ħω/{exp[ħω/(kBT)]−1}为普朗克谐振子能量,ħ为约化普朗克常数,kB为玻尔兹曼常数,T为热力学温度.Θ与Im{ε}的乘积揭示了电流源项的光谱强度受温度和材料物性的影响规律.为避免电流源项的光谱相关性在FDTD算法中需要作额外傅里叶变换,本文使用Luo等[20]提出的Langevin法,以随机白噪声¯J作为计算中采用的实际源项形式,其特点是电流源光谱强度归一化,彼此非相干,
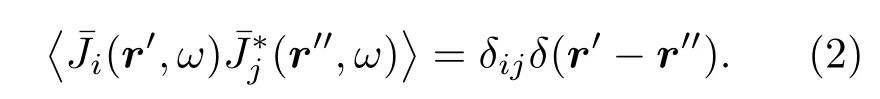
在计算结束的后处理中,根据(1)式和(2)式的系数之比对热流结果进行反归一化,即得到正确结果.实际在离散网格时间域模拟中,在发射体内部填充的电流源项是单位振幅、相位随机的高斯脉冲形式,使其在数值意义上逼近(2)式所要求的非相干性;计算时每个算例都运行多次模拟取平均,消除单次模拟中随机噪声的影响,如图3(a)所示,本文算例在30—40次模拟后收敛.除源项处理部分外,本文FDTD方法架构与常规方法一致,计算随机电流源激发的真空间隙中的电磁场强度,叉乘得到坡印廷矢量,即得到通过近场空隙的辐射热流.物质的色散特性用Drude-Lorentz模型描述,并使用分段线性递归卷积(PLRC)方法完成频域到时间域的变换处理.物质介电常数的Drude-Lorentz模型表达式为
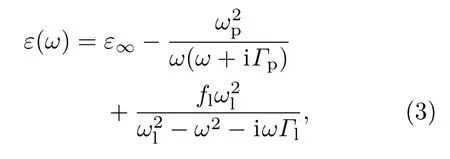
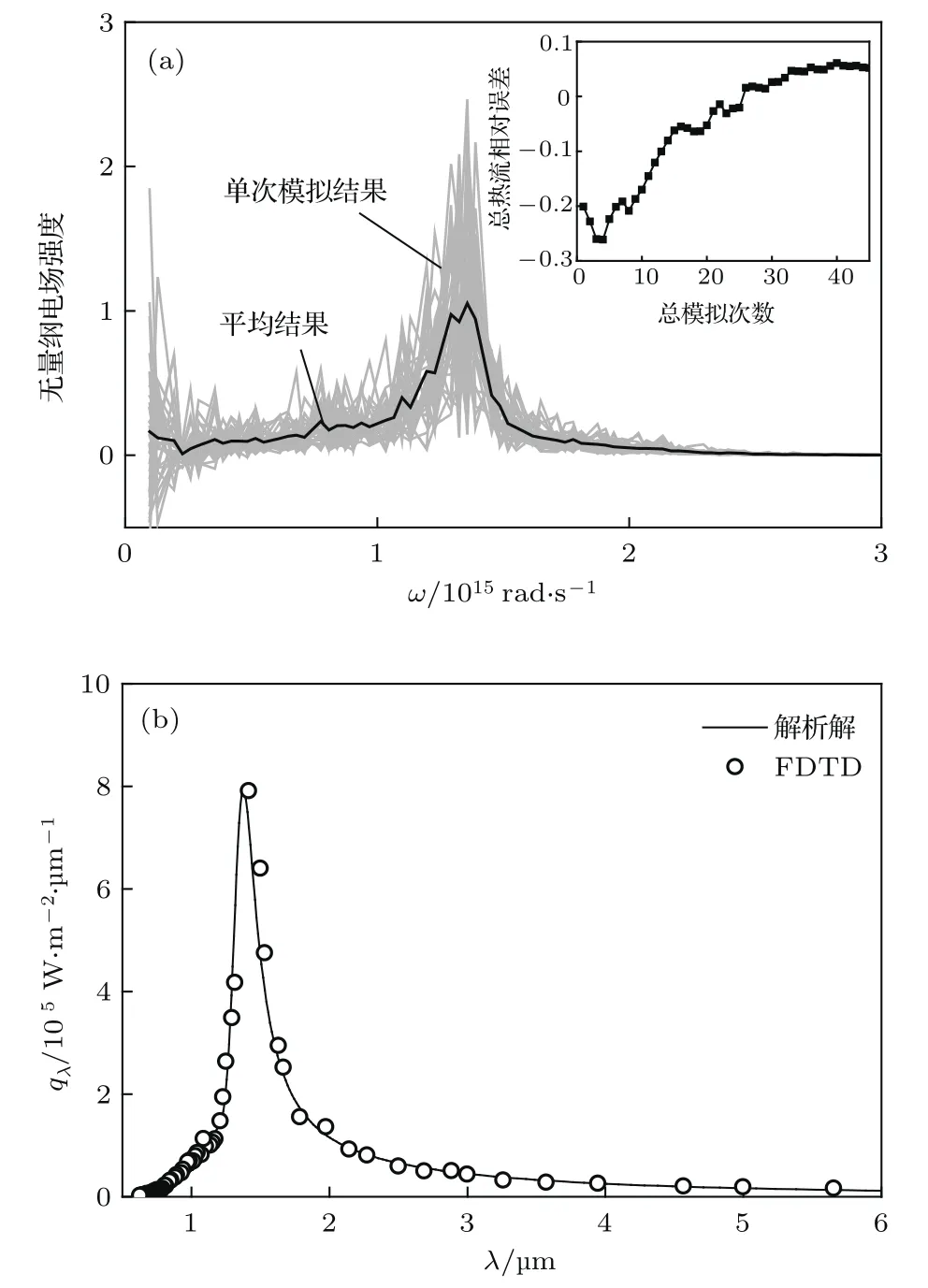
图3 近场FDTD算法验证 (a)Langevin法过程与收敛速率展示;(b)FDTD与解析解对比计算GZO平板间的近场辐射热流Fig.3.Validation of the near- fi eld FDTD calculation:(a)Illustration of Langevin approach and numerical convergence;(b)comparison of FDTD and analytical results for radiative transfer between GZO plates.
式中ωp为等离子振荡频率,ωl为Lorentz谐振频率,Γp和Γl为阻尼系数.计算中使用的拟合参数如表1所示.

表1 计算中使用的物质Drude-Lorentz模型参数Table 1.Drude-Lorentz parameters for all materials used in calculation.
此外,虽然是周期性结构模拟,但由于电流源项具有不同波数分量,因此不能直接使用x,y方向的Bloch周期边界条件;模拟域中包含数个结构周期,边界均使用完美匹配层(PML)条件[30]吸收向外传递的电磁波.模拟域尺寸为x=y=2.5µm,z=1.2µm,经检验三个维度上尺寸分别加倍不会导致结果显著变化.网格边长为10 nm,计算结果取48次模拟平均值,单次模拟在Intel E5-2630 v3 CPU上单核运行时间48—60 h.图3(b)中以GZO平板间近场辐射传热为算例,与解析解进行对比,验证了近场FDTD结果的准确性.
3 计算结果与物理机理分析
3.1 半无限大GaSb电池
借助近场FDTD方法阐明添加表面光栅结构对GaSb吸收能力的影响.为使电池表面的光栅结构与发射体表面波激发的交替正负电荷聚集区域充分耦合,光栅周期Λ应设计为SPP的半波长.由SPP的色散关系得到其波长为[11]

式中SPP频率ωSPP=1.39×1015rad/s,c为真空光速,ε0=1为真空相对介电常数. 由此可得λSPP=829 nm,为方便网格离散近似取Λ=400 nm.考虑结构加工的可行性,光栅高度不宜过大,计算中取h=200 nm,检验发现当h进一步增加时对结果影响不显著.
在固定结构参数Λ,h的取值后,重点研究顶端边长a的取值影响.对于有结构GaSb,不能用平行平板间的解析解验证FDTD数值解的准确性,使用文献[31]中的FMM半解析解作为对比.图4所示为两种典型参数条件下光栅结构对近场辐射热流的影响,其中a=320 nm代表高填充比例(f=0.64)、光栅沟槽高宽比大(h/w=2.5)的情况,a=200 nm代表低填充比例(f=0.25)、光栅沟槽高宽比小(h/w=1.0)的情况.从图4(a)可以看出,GaSb表面添加光栅结构有效提高了热流的峰值和波长的选择性,且FDTD结果与FMM符合良好,长波区FDTD热流结果略偏低是因为模拟区域尺寸受内存限制,长波区计算精度降低.

图4 表面光栅结构对GZO与GaSb间的辐射热流影响(Λ=400 nm,h=200 nm) (a)光谱热流结果;(b)相对使用远场黑体发射器的热流比值Fig.4. Radiative heat transfer between GZO and GaSb with and without surface structure(Λ =400 nm,h=200 nm):(a)Spectral radiative heat fl ux;(b)ratio over the condition using far- fi eld blackbody emitter.
为突出参数影响,图4(b)展示了近场热流与同温度远场黑体发射器到无结构GaSb热流的比值.可见GZO到无结构GaSb的近场热流已经在电池能带内超过了黑体辐射情况,而添加GaSb表面结构又显著增加了热流峰值.其中,高填充比例的光栅参数对应较高的峰值热流,a=320 nm时峰值热流达到远场黑体的2倍以上,是算例中峰值热流最高的情况,但热流增益光谱较宽,也增加了能带以外的长波区的辐射传热,影响了能量转化效率的提升.低填充比例(a=200 nm)时热流峰值略低,但光谱选择性更好,相比无结构情况的热流增益全部位于电池能带内,能够实现更高的能量转化效率.
3.2 表面减反射物理机理
相比其他计算方法,FDTD作为时域模拟方法能够清晰展示电磁场的时间演化规律,适于解释与表面波传播相关的物理现象,这也是使用FDTD法的重要原因.为揭示GaSb表面光栅操控近场辐射热流的物理机理,在FDTD的发射器表面中央添加单一电偶极子源项,设定其频率为GZO的SPP频率,观察一个时间周期内的电场强度变化(图5(a)).单点源项在GZO表面激发了正负电荷交替的聚集区,随时间推移沿表面方向传播,体现了GZO在近红外波段的SPP特性,正负电荷的周期长度即为表面波波长.而在与GZO间隔200 nm的GaSb侧,表面周期栅格结构的沟槽中同样形成了电荷聚集,这是介电常数周期变化结构的陷光效应.除了正对偶极子的沟槽直接受点源影响外,两侧沟槽中电荷的符号与正对的GZO恰好相反,这是与GZO表面波跨越近场间隙耦合作用的结果,且间隙两侧电荷分布的空间周期一致,因此可随时间演化保持稳定的近场间隙两侧电荷异号关系,辅助电磁波从发射器到吸收器的传输,由此增加SPP频率附近的辐射热流.物理机理简化过程如图5(b)所示.
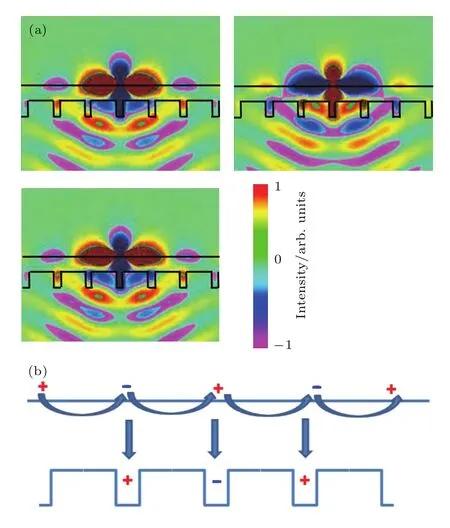
图5 单偶极子源项情形的时间域结果 (a)一个时间周期内的电场强度演化;(b)电荷分布简化示意图Fig.5. FDTD simulation with a single dipole source:(a)Evolution of electric fi eld intensity within one time period;(b)simpli fi ed illustration of charge distribution.
时域模拟结果说明了GaSb表面光栅调制近场辐射热流的物理机理,即周期结构与发射器SPP耦合的陷光效应.为验证光谱调制是发射器、吸收器两端在近场间距耦合的结果,图6给出了不同近场间距下的光谱热流计算结果.GZO与GaSb距离很近(d=100—200 nm)时,辐射热流在GZO的SPP位置附近有很高的峰值,而随着间距增大,辐射热流绝对值和光谱选择性均迅速减弱,在d=1µm时热流峰值已经完全消失.这证明了本文的光谱调控策略是一种特别适用于近场辐射传热的有效方法,只有发射器和吸收器间隔在近场尺度耦合才会诱发这种物理现象.
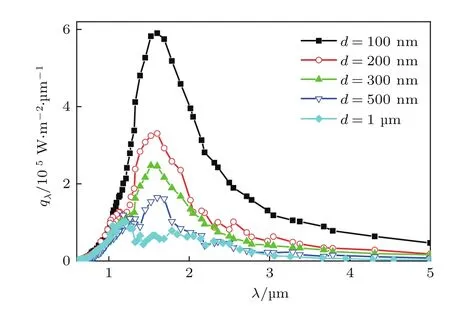
图6 不同近场间距下GZO与GaSb间的辐射热流(Λ=400 nm,a=320 nm,h=200 nm)Fig.6.Radiative heat fl ux between GZO and GaSb with various d(Λ=400 nm,a=320 nm,h=200 nm).
3.3 有限厚度GaSb电池
在添加GaSb表面结构的基础上,可进一步将电池薄膜化,在高反射率的金属基底上制备超薄膜III-V族半导体电池(图7(a)),通过内全反射实现光谱选择性吸收,提升光谱操控幅度[32].图7(b)对比了无限厚与有限厚GaSb电池的近场辐射热流,共同参数为Λ=400 nm,a=320 nm;对无限厚GaSb电池取h=200 nm,而对有限厚GaSb电池经优化计算取h1=100 nm,h2=250 nm.结果显示使用超薄膜GaSb电池配合高反射率金属底板进一步提升了辐射热流的峰值和光谱选择性,与远场黑体热流比值达到2.84,且增益区域全部位于电池能带内,同时实现了高辐射功率与高转化效率.
为说明基于严格结构的计算方法对揭示物理机理的意义,图7(b)对比了两种近场辐射传热的常用近似计算方法——EMT与Derjaguin近似[29].其中,EMT将非均匀介质层近似为具有等效介电常数的均匀介质,再应用一维结构解析解计算辐射热流;对比采用各向异性的Maxwell等效法则,这是一种精度较高、适用范围广的EMT法则.Derjaguin理论则分别计算近场间距为d和d+h1的一维解,再根据光栅填充比例取加权平均.对比可见两种近似方法均效果不佳,Derjaguin近似低估了全波段热流,而EMT热流结果过高且峰值位置有偏差,原因在于光栅层被等效为均匀的理想低折射率减反射层.这一结论与文献[29]中金属表面结构对近场辐射热流的影响相似,也再次证明了GaSb表面光栅对近场辐射热流的操控是由x,y方向介电常数的非均匀性引起的,使用近似方法不能描述电磁波与非均匀结构的作用机理,会对计算结果精度造成严重影响.

图7 使用有限厚度GaSb作为吸收器的辐射热流计算 (a)尺寸参数示意图;(b)辐射热流计算结果与近似方法的比较Fig.7.Radiative heat fl ux computation using GaSb absorber with fi nite thickness:(a)Illustration of size parameters;(b)radiative fl ux results compared with estimation methods.
4 结 论
设计了表面光栅结构用于增加GaSb对近场辐射传热的吸收能力,与具有近红外SPP特性的GZO发射器搭配,作为提升近场热光伏系统输出功率和能源转化效率的方案.使用结合涨落耗散定律的随机FDTD方法,直接对有复杂结构参与的近场辐射传热进行严格计算,时域和频域模拟结果揭示了一种新的近场辐射光谱调控机理,即与表面波耦合的陷光效应.将表面光栅结构与超薄膜电池结合,增强了辐射热流光谱的调控幅度,使近场热流峰值达到使用同温度远场黑体辐射源情况下的2.84倍,且热流增益区域全部位于波长略短于电池能带的窄波段,由此可有效提升近场热光伏系统的输出效率和转换功率.
[1]Liu D,Yu H T,Yang Z,Duan Y Y 2015J.Eng.Thermophys.36 698(in Chinese)[刘东,于海童,杨震,段远源2015工程热物理学报36 698]
[2]Coutts T J 1999Renewable and Sustainable Energy Reviews3 77
[3]Lenert A,Bierman D M,Nam Y,Chan W R,Celanovi C I,Soljačić M,Wang E N 2014Nat.Nanotechnol.9 126
[4]Basu S,Chen Y,Zhang Z M 2007Int.J.Energ.Res.31 689
[5]Hanamura K,Fukai H,Srinivasan E,Asano M,Masuhara T 2011ASME/JSME 8th Thermal Engineering Joint ConferenceHawaii,USA,March 2011
[6]Geng C,Zheng Y,Zhang Y Z,Yan H 2016Acta Phys.Sin.65 070201(in Chinese)[耿超,郑义,张永哲,严辉2016物理学报65 070201]
[7]Ijiro T,Yamada N 2015Appl.Phys.Lett.106 23103
[8]Chalabi H,Hasman E,Brongersma M L 2015Phys.Rev.B91 14302
[9]Molesky S,Jacob Z 2015Phys.Rev.B91 205435
[10]Lu D,Das A,Park W 2017Opt.Express25 12999
[11]Zhang Z M 2007Nano/Microscale Heat Transfer(New York:McGraw-Hill)p377
[12]Francoeur M,Mengüç M P,Vaillon R 2009J.Quant.Spectr.Radiat.Transfer110 2002
[13]Li J Y,Xuan Y M,Li Q,Han Y G 2013J.Eng.Thermophys.34 1548(in Chinese)[李佳玉,宣益民,李强,韩玉阁2013工程热物理学报34 1548]
[14]Wu H H,Huang Y,Zhu K Y 2016J.Eng.Thermophys.37 597(in Chinese)[吴会海,黄勇,朱克勇2016工程热物理学报37 597]
[15]Zhu K Y,Huang Y,Wu H H 2016J.Eng.Thermophys.37 2393(in Chinese)[朱克勇,黄勇,吴会海 2016工程热物理学报37 2393]
[16]Vongsoasup N,Francoeur M,Hanamura K 2017Int.J.Heat Mass Transfer115 326
[17]Chang J Y,Yang Y,Wang L 2015Int.J.Heat Mass Transfer87 237
[18]Zhang R Z,Zhang Z M 2017J.Quant.Spectr.Radiat.Transfer197 132
[19]Yu H T,Liu D,Duan Y Y,Zhen Y 2015Int.J.Heat Mass Transfer87 303
[20]Luo C,Narayanaswamy A,Chen G,Joannopoulos J D 2004Phys.Rev.Lett.93 213905
[21]Lussange J,Guérout R,Rosa F S S,Greffet J J,Lambrecht A,Reynaud S 2012Phys.Rev.B86 85432
[22]Bai Y,Jiang Y,Liu L 2015J.Quant.Spectr.Radiat.Transfer158 36
[23]Kanamori Y,Kobayashi K,Yugami H,Hane K 2003Jpn.J.Appl.Phys.42 4020
[24]Bernardi M P,Dupré O,Blandre E,Chapuis P O,Vaillon R,Francoeur M 2015Sci.Rep.5 11626
[25]Didari A,Mengüç M P 2017J.Quant.Spectr.Radiat.Transfer197 95
[26]Datas A,Hirashima D,Hanamura K 2013J.Therm.Sci.Tech.8 91
[27]Kim J,Naik G V,Emani N K,Guler U,Boltasseva A 2013IEEE J.Sel.Top.Quant.19 4601907
[28]Djurišić A B,Li E H,Raki C D,Majewski M L 2000Appl.Phys.A70 29
[29]Yang Y,Wang L 2016Phys.Rev.Lett.117 44301
[30]Wei B,Li X Y,Wang F,Ge D B 2009Acta Phys.Sin.58 6174(in Chinese)[魏兵,李小勇,王飞,葛德彪2009物理学报58 6174]
[31]Yu H,Liu D,Yang Z,Duan Y 2017Sci.Rep.7 1026
[32]Kim J,Hwang J,Song K,Kim N,Shin J C,Lee J 2016Appl.Phys.Lett.108 253101
