锥形二维光子晶体太阳电池数值模拟∗

陈培专 于莉媛 牛萍娟 付贤松 杨广华张建军 侯国付

1)(天津工业大学电气工程与自动化学院,大功率半导体照明应用系统教育部工程中心,天津 300387)

2)(南开大学,光电子薄膜器件与技术研究所,光电子薄膜器件与技术天津市重点实验室,光学信息技术科学教育部重点实验室,天津 300071)

1 引 言

相比于晶硅太阳电池,硅基薄膜太阳电池吸收层较薄,原材料使用量少,因此在成本下降空间上具有很大的优势[1,2].但是所有类型的硅基薄膜太阳电池普遍存在一个问题,即随着波长的增大,吸收层材料的吸收系数迅速下降,导致电池的长波吸收不断减小[3,4].对于单结硅基薄膜太阳电池,要将光谱吸收范围内的光充分吸收,吸收层厚度要达到毫米量级[5].但是由于制备工艺的原因,硅基薄膜太阳电池的吸收层晶格结构无法达到晶硅电池水平,因此存在较多的缺陷态,载流子扩散长度较小.为了充分收集光生载流子,吸收层厚度必须控制在几百纳米至几微米的范围内,这会导致光学吸收和载流子收集之间的矛盾.为了解决这一矛盾,需要在电池中引入陷光结构,在不增加甚至减小吸收层厚度的情况下,使更多的光进入电池内部并延长光在电池内部的吸收光程,实现光厚电薄[4,6−8].

硅基薄膜太阳电池的陷光结构包含两种类型:随机绒面结构[3,9,10]和周期性绒面结构[11−13].周期性绒面结构在两个方向上具有周期性,实质上属于微米或亚微米级的二维光子晶体(twodimensional photonic crystal,2D PC)[14,15].在之前的研究中,通常采用散射光占总反射光或透射光的比率即绒度来表征绒面形貌陷光能力的优劣[9,16−18].绒度越高,则绒面形貌的陷光能力越强,电池吸收越好.同时研究认为,长波陷光需要大特征尺寸的绒面形貌,而短波陷光需要小特征尺寸的绒面形貌[16−18].以上结论来自于实验中获取的经验,但实际上并不能完全适用于所有的随机绒面结构,尤其是不能适用于周期性结构[19].原因在于这些研究通常只关注绒面的横向特征尺寸.但是绒度的大小不仅与绒面形貌的横向特征尺寸(周期)相关,还与绒面形貌的高度直接相关[20].不同的绒面特征尺寸和绒面高度相结合可以形成相同的绒度,但对于电池的陷光效果是完全不同的.由此也导致到目前为止仍然无法了解何种绒面形貌具有最佳的陷光效果.

相比于随机绒面结构,采用周期绒面即2D PC的陷光结构有一个优势,即易于采用波动光学模拟的办法,通过严格求解麦克斯韦方程组,探索结构参数变化对电池吸收的影响规律,从而获得电池最佳的陷光形貌.事实上,随机绒面结构可以看作一系列正弦型周期性结构经空间傅里叶变换叠加形成[21].因此,获悉最佳的周期结构对后续研究并设计最佳的随机绒面结构也有很大的帮助.随机绒面结构的特征尺寸与太阳电池的光谱吸收范围属于同一个量级,本质上讲也属于波动光学的范畴.但在目前对周期绒面结构即2D PC的模拟研究中通常不考虑背电极、前电极、p型层和n型层等支持层的影响,只是简单研究绒面形貌结构参数变化对电池本征吸收的影响[22−25].实际上周期陷光形貌在提升电池总吸收的同时,也会显著提升支持层的寄生吸收,由此导致所得的最佳形貌未必能显著提升本征吸收.此外,对于周期结构而言,其陷光效果主要取决于衍射角和对应的衍射效率,这二者又主要取决于周期尺寸和高度.在先前的研究中通常将周期尺寸和高度对电池短路电流密度的影响进行分立研究,因此获得的结论具有片面性,无法真正洞悉绒面形貌对电池光学吸收的影响规律[26,27].

本文基于波动光学理论,采用时域有限差分( fi nite-difference time-domain,FDTD)方法,模拟研究锥形2D PC结构参数对单结微晶硅太阳电池各膜层吸收的影响规律.通过引入纵横比(高度与周期的比值)的概念,将周期和高度对电池各膜层吸收的影响有机结合,提出新的陷光思路,为实验获取优异的周期或随机绒面陷光结构提供指导.首先研究在不同波长范围内,周期和纵横比(≤1)变化对电池各膜层吸收和总吸收的影响规律;而后研究占空比变化对各膜层吸收和总吸收的影响;最后基于优化的周期和占空比,探讨纵横比大于1时电池吸收随纵横比的变化规律.

2 模拟及验证

2.1 模拟方法

基于Lumerical公司的商业化FDTD计算软件(FDTD Solutions),模拟研究计算锥形2D PC结构参数变化对电池各膜层吸收和总吸收的影响规律.随着计算机技术的飞速进步,FDTD数值计算方法得到了迅猛发展,应用范围几乎涉及所有电磁领域,是目前计算电磁学界公认的、最受关注的算法[28].应用FDTD算法求解太阳电池问题时,算法在模拟区域自动划分网格(Yee元胞),而后电磁场便从激励源处开始随时间逐步推进,待电磁场稳定后自动停止运算,此时便可获得太阳电池任何位置的电磁场信息.各膜层吸收Pabs的计算公式为[29]

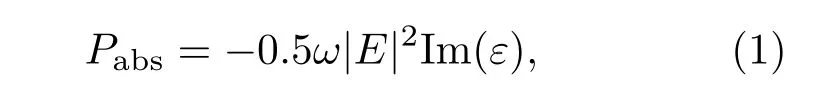
式中|E|2为电场强度,Im(ε)为材料介电常数ε的虚部,和消光系数直接相关,ω为频率.获得电池的空间电场分布|E|后即可计算得到各膜层的吸收.为了探讨2D PC结构参数变化对各膜层吸收的影响规律,将各膜层吸收转化为短路电流密度(Jsc),即一个结构参数下的每一膜层吸收只对应一个Jsc.具体方法如下.

假设各膜层吸收的光子都能产生电子空穴对,且一个光子产生一个电子空穴对,即电子空穴产生率η0=1,则电池各膜层的量子效率曲线EQ(λ)可表示为

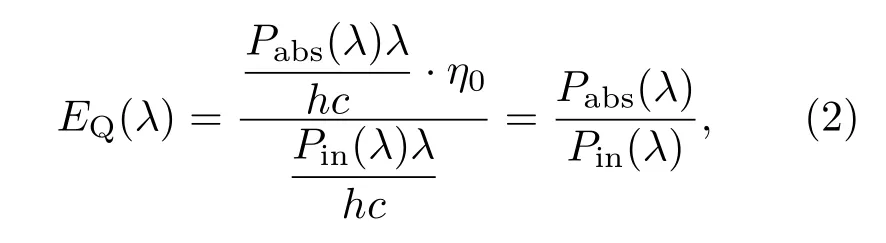
式中Pin(λ)和Pabs(λ)分别为波长λ时的入射光光场强度和被各膜层吸收的光场强度,h为普朗克常数,c为真空中的光速.将EQ(λ)和AM1.5标准太阳光谱进行积分,即可获得各膜层产生的短路电流密度Jsc,表达式为

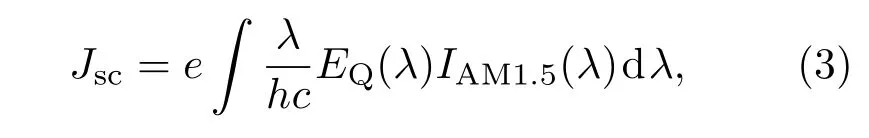
式中e为电子电量,IAM1.5为AM1.5标准太阳光谱(来自ASTM G173-03,由美国可再生能源实验室NREL测试获得).

2.2 模拟结构

选择具有宽谱域光谱吸收范围(300—1100 nm)的n-i-p型单结微晶硅(µc-Si:H)太阳电池作为研究对象,其本征层厚度通常约为2µm.当衬底引入绒面陷光形貌时,银(Ag)背反射电极会产生等离子激元共振吸收,并且随着粗糙度的增大,等离子激元共振吸收也会增强[30].此外,在绒面形貌上沉积微晶硅电池时,由于本征层厚度较厚和晶粒生长方向的影响,基底形貌并不能得以保持.为了充分了解陷光机理,减少寄生吸收的影响,并考虑到要对实验有一定的指导性,选择在本征吸收层引入锥形二维光子晶体,以膜层后缀名添加_PC表示,如i-µc-Si_PC.电池具体结构为平面衬底/Ag(100 nm)/ZnO:Al(AZO,100 nm)/n-a-Si(20 nm)/i-µc-Si_base(100 nm)/i-µc-Si_PC(2 µm)/p-nc-Si(20 nm)/ITO(80 nm).模拟制备流程如图1所示.首先在平面基底上顺序沉积Ag/AZO复合背反射电极、n型层、本征层(i-µc-Si_base和i-µc-Si_PC),如图1(a)所示;然后假设采用光刻等方法在i-µc-Si_PC上刻蚀形成锥形光子晶体(图1(b));最后再沉积p型层和ITO(图1(c)). 图中的i-µc-Si分为两部分:一部分是i-µc-Si_PC,厚度固定为2µm,只在该层上刻蚀制备光子晶体形貌,也即光子晶体的最大高度为2µm;另一部分是i-µc-Si_base,厚度固定为100 nm(不做刻蚀),该部分主要起阻挡层作用,即当i-µc-Si_PC的刻蚀高度达到2µm时,防止前后电极相接触而发生短路.

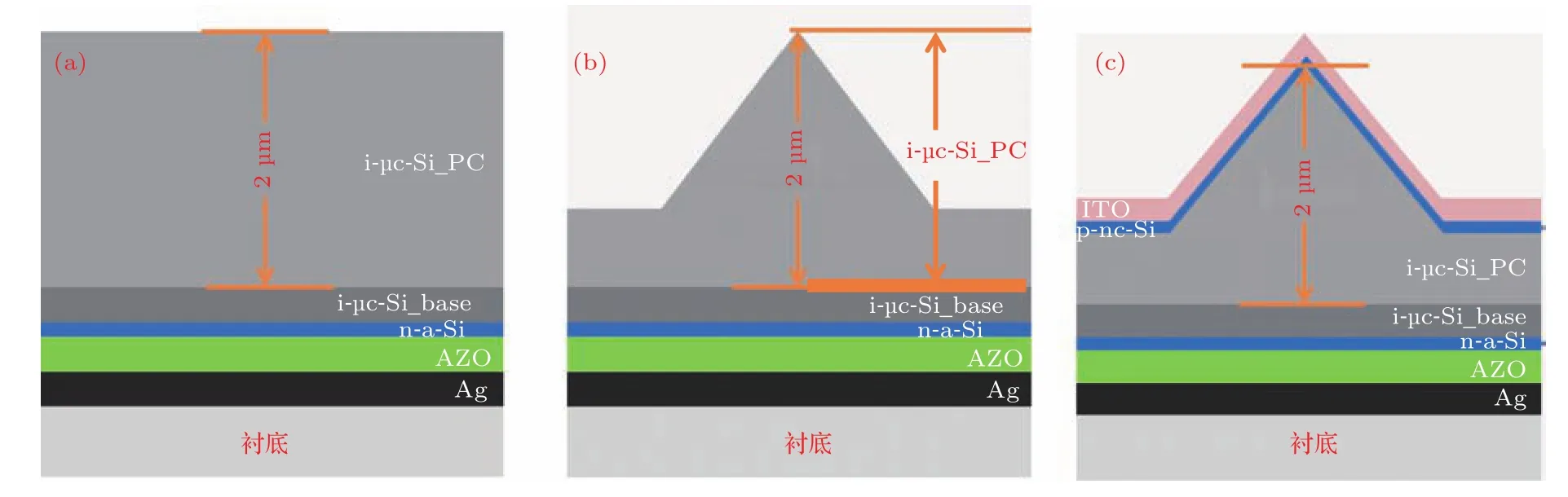
图1 基于锥形2D PC吸收层的单结微晶硅电池模拟制备流程图 (a)本征层(i-µc-Si_PC)未形成锥形2D PC;(b)本征层形成锥形2D PC;(c)完整电池结构Fig.1.Schematic of fabricating microcrystalline silicon thin fi lm solar cells based on conical 2D PC:(a)Intrinsic layer(i-µc-Si_PC)without 2D PC;(b)intrinsic layer with 2D PC;(c)complete cell with 2D PC intrinsic layer.

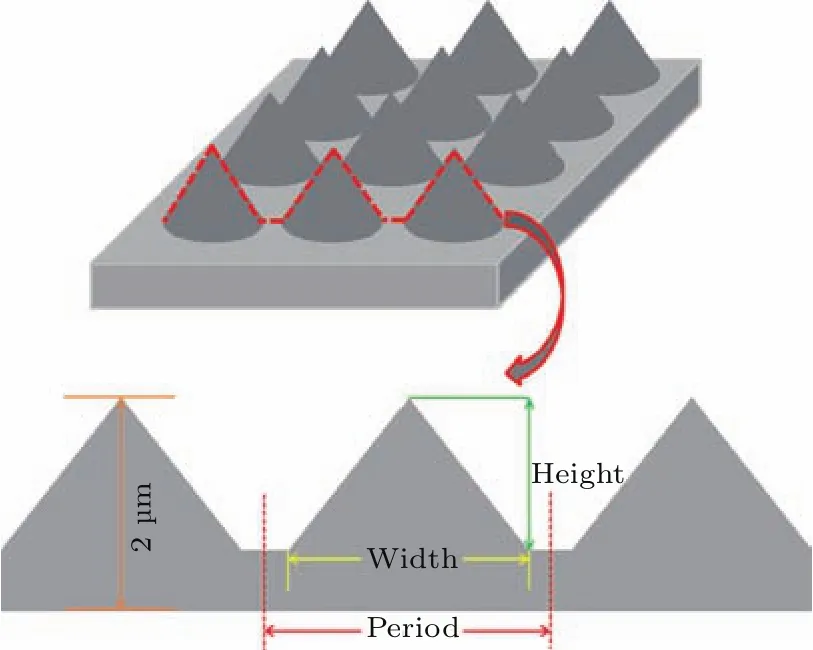
图2 锥形i-µc-Si_PC结构示意图Fig.2.Structure schematic of conical i-µc-Si_PC.

图2为i-µc-Si_PC的结构示意图,其总高度保持2µm不变,实验中可以通过刻蚀等方法在该层上形成不同的锥形2D PC结构.两个相邻的锥体并不直接接触形成V型底,而是留出一定的距离形成U型底结构,即底宽(W)小于周期(P),二者的比值为占空比ff(ff=W/P).锥体的高度(H)最大值为2µm,其与周期的比值定义为纵横比rHP(rHP=H/P).

2.3 模拟验证

为了提升模拟的准确性及可指导性,模拟计算时所用到的随波长变化的各材料均由南开大学光电子所实际制备,而后采用商用光谱椭偏仪WVASE32测试得到材料的椭偏量Ψ和Δ,并运用Tauc-Lorentz模型进行拟合获得材料光学常数,如图3所示.所有硅基膜层均采用等离子体增强化学气相沉积(RF-PECVD)系统制备,Ag,AZO采用磁控溅射方法沉积,ITO则用热蒸发法制备.

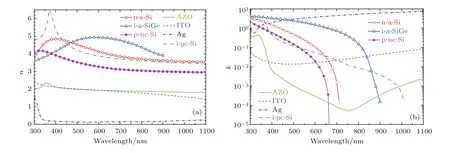
图3 各膜层材料光学常数 (a)折射率n;(b)消光系数kFig.3.Optical constants as a function of wavelength for each thin fi lm layer:(a)Refractive index n;(b)extinction coefficient k.

为了验证模拟的准确性,在图4(a)所示锥形光子晶体基底上(P=3µm,H=1µm,ff=13/15)沉积单结非晶硅锗电池,电池结构为Ag(100 nm)/AZO(100 nm)/n-a-Si(20 nm)/i-a-SiGe:H(200 nm)/p-nc-Si(15 nm)/ITO(80 nm),而后用FDTD模拟计算对应结构电池的量子效率,并与实验值进行比较,如图4(b)所示.之所以选择在上述基底上沉积非晶硅锗而非微晶硅,主要原因是前者吸收层较薄,可以实现保形生长,易于设计模拟结构并和实验结果进行有效比较.从图4(a)也可以看出沉积电池后基底形貌得以较好保持.为了减少数据量,所做的模拟计算都是基于二维模拟.图4(b)中EQ曲线实验值是在−0.3 V偏压下测试获得的,主要目的是减小p/i界面对载流子输运的影响以及电极欧姆接触对载流子收集的影响,使实验值更接近理想状况.从图中可以看出,模拟值和实验值符合较好,积分电流值分别为19.5 mA/cm2(模拟)和19.2 mA/cm2(实验),说明模拟结果可靠性较高.二者的差别主要在于短波范围,很重要的一个原因是沉积时厚度不能完全精确控制,会和模拟时设置的厚度有所偏差,尤其是对于厚度只有几十纳米的p型层和ITO而言更容易引起偏离,而这二者厚度稍微有所偏差就会对短波吸收造成重要影响.

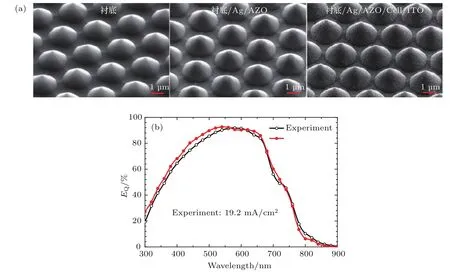
图4 (a)锥形光子晶体衬底及在衬底上沉积背反射电极和电池时扫描电子显微镜俯视图(45°角);(b)模拟和实验的EQ结果比较Fig.4.(a)Scanning electron microscopic image of conical 2D PC substrate and conical 2D PC substrates with back re fl ector and cells deposited on it,respectively;(b)EQcurves for simulation and experiment.

3 结果与讨论

3.1 周期和纵横比对电池各膜层吸收和总吸收的影响

锥形2D PC吸收层主要有三个结构参数:周期P、高度H和占空比ff,如图2所示.如果分立研究各膜层吸收随P或H的变化,或者采用三维坐标研究吸收随P和H的变化,都无法探究其中内在的规律.为此,将周期和高度相结合,引入纵横比rHP,着重研究各膜层光学吸收随P和rHP的变化规律.在研究二者对电池吸收的影响时,将ff暂时固定为13/15,周期P在0.25—2.00µm区间变化,步长为0.25µm;纵横比rHP选择为1/6,1/3,1/2,2/3,5/6,1/1这6个值,步长为1/6.

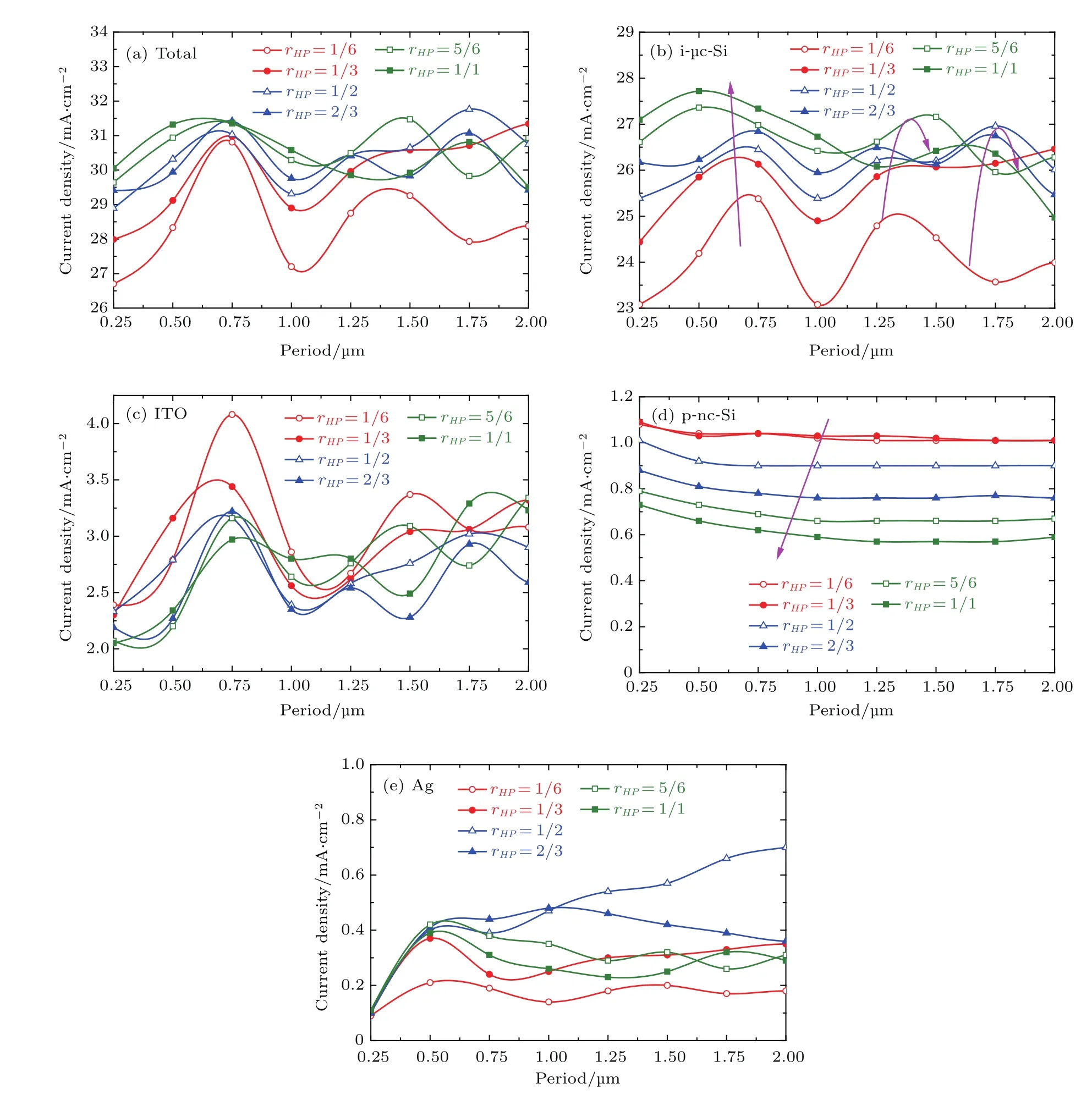
图5 光谱积分波长范围为300—1100 nm时,在不同的纵横比rHP下,周期P变化对微晶硅电池各膜层吸收(Jsc)的影响(a)总吸收;(b)i-µc-Si(包含 i-µc-Si_base和i-µc-Si_PC两部分);(c)ITO;(d)p-nc-Si;(e)AgFig.5.Influence of period P on each layer absorption of the microcrystalline solar cells at different aspect ratio rHPwith integral wavelength region of 300–1100 nm:(a)Total absorption;(b)i-µc-Si(both i-µc-Si_base and i-µc-Si_PC);(c)ITO;(d)p-nc-Si;(e)Ag.

图5所示为光谱积分波长范围为300—1100 nm时,在不同的纵横比下周期变化对微晶硅电池各膜层吸收(Jsc)的影响.其中图5(a)为总吸收, 图5(b)为i-µc-Si吸收(包含i-µc-Si_base和i-µc-Si_PC两部分),图5(c)为ITO吸收,图5(d)为p-nc-Si吸收,图5(e)为Ag吸收.没有给出AZO和n-a-Si的吸收曲线,因为无论采用何种结构参数,AZO和n-a-Si的寄生吸收都非常小,可以忽略不计.

当纵横比不变时,本征层吸收随着周期增大呈正弦变化.其余膜层吸收和电池总吸收也有类似的变化趋势,说明衍射效果随着周期增大呈正弦变化,而且会作用在各个膜层上.随着纵横比的增大,图5(a)中的总吸收曲线和图5(b)中的本征吸收曲线变化趋势非常相似.当P≤1.0µm时,电池的本征吸收随着纵横比的增大不断上升,在rHP=1时实现最大化;当1.0µm＜P≤1.5µm时,本征吸收随着纵横比的增大先不断上升而后减小,在rHP=5/6时实现最大化;当1.5µm＜P≤2.0µm时,本征吸收随纵横比的增大仍然先上升后下降,但实现最大化的纵横比减小为1/2.这说明要实现本征吸收最大化,小周期应采用大纵横比,大周期则应减小纵横比.

当纵横比和周期发生变化时,ITO的寄生吸收介于2.5—4.0 mA/cm2之间.对于p-nc-Si,当纵横比不变时,周期变化对其寄生吸收基本没有影响;纵横比增大时,寄生吸收总体呈逐渐下降趋势,贡献的寄生电流为0.6—1.0 mA/cm2.由此可见,周期和纵横比变化对p-nc-Si的寄生吸收影响很小.从图5(e)可以看出,纵横比变化包括周期变化对Ag的寄生吸收影响都很小,损耗电流不超过0.7 mA/cm2.这说明采用平面基底,使吸收和陷光同时在本征层中进行,可以显著减小Ag的寄生吸收.综上可以看出,对于锥形2D PC吸收层电池,寄生吸收主要由ITO引起.要减小ITO的寄生吸收,关键是减小ITO的吸收系数.

根据图5(b)可知,当P=0.5µm,rHP=1时,电池的本征吸收达到峰值,Jsc为27.8 mA/cm2;与平面结构相比(吸收层厚度为2.1µm,Jsc为21.9 mA/cm2),Jsc提升5.8 mA/cm2,相对增加27%.图6为以上2D PC结构电池和平面结构电池的本征吸收对比曲线.从图中可以看出,在吸收层中引入上述结构的2D PC,本征吸收获得显著提升.在300—550 nm波长范围内,到达电池底部的光很少,因此电池的吸收变化主要由电池的前表面反射变化引起.当波长大于550 nm时,大部分入射光能到达电池底部,此时背反射电极的反射和本征层的陷光特性对电池吸收起主要作用.在此波长范围内,本征吸收曲线出现很多吸收增强峰,主要是由锥形PC吸收层的振动模引起.为了进一步探寻锥形2D PC吸收层的陷光规律,分别研究300—550 nm(短波),550—800 nm(中波)和800—1100 nm(长波)这三个波长范围内锥形2D PC的周期和纵横比变化对电池本征吸收的影响,如图7所示.

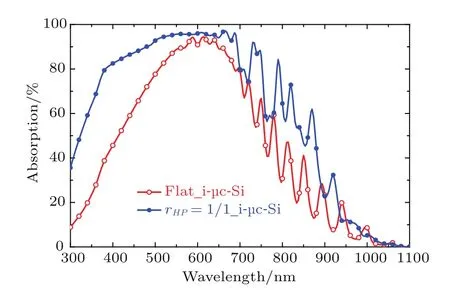
图6 锥形2D PC结构(P=0.5µm,rHP=1)和平面结构本征吸收比较Fig.6.Intrinsic absorptions of cells with and without 2D PC( fl at).

在300—550 nm波长范围内,Ag的寄生吸收为0,因为没有光到达电池底部.从图7(a)可以看出,随着纵横比的增大,本征吸收先迅速上升;当纵横比达到并超过1/2时,本征吸收上升幅度不断减小.此外,在上述波长范围内,当纵横比不变时,本征吸收受周期变化的影响很小.因此,为了使电池的短波吸收达到最大化,锥形2D PC吸收层可以采用任意周期,同时设定rHP＞1/2即可.该结论也表明,为了使更多的光进入电池内部而在电池表面引入绒面减反膜时,重点在于优化绒面形貌的纵横比,使之超过1/2.

在550—800 nm波长范围内,从图7(b)可以看出,当0.25µm ≤P＜0.75µm,rHP≥ 5/6时,电池的本征吸收明显高于其他周期和纵横比的电池对应吸收.说明在上述参数范围内,锥形2D PC的波动效果最强,电池陷光效果最好.在800—1100 nm波长范围内,本征吸收主要受周期大小的影响,受纵横比的影响较小,当0.50µm≤P≤0.75µm时本征吸收最高.

综合波长范围550—800 nm和800—1100 nm的本征吸收可以得出,当锥形2D PC吸收层的周期在0.5µm左右,且纵横比较大时,在中长波范围内电池的陷光效果最好.而当波长为300—550 nm时,本征吸收受周期的影响很小,但随纵横比的增大先上升而后逐渐趋于稳定.故对于锥形2D PC本征微晶硅电池,最佳的锥形2D PC结构应设置周期约为0.5µm,并选择大纵横比(由于在前述研究中纵横比最大只为1,纵横比超过1时是否会继续提升吸收将于后续讨论).

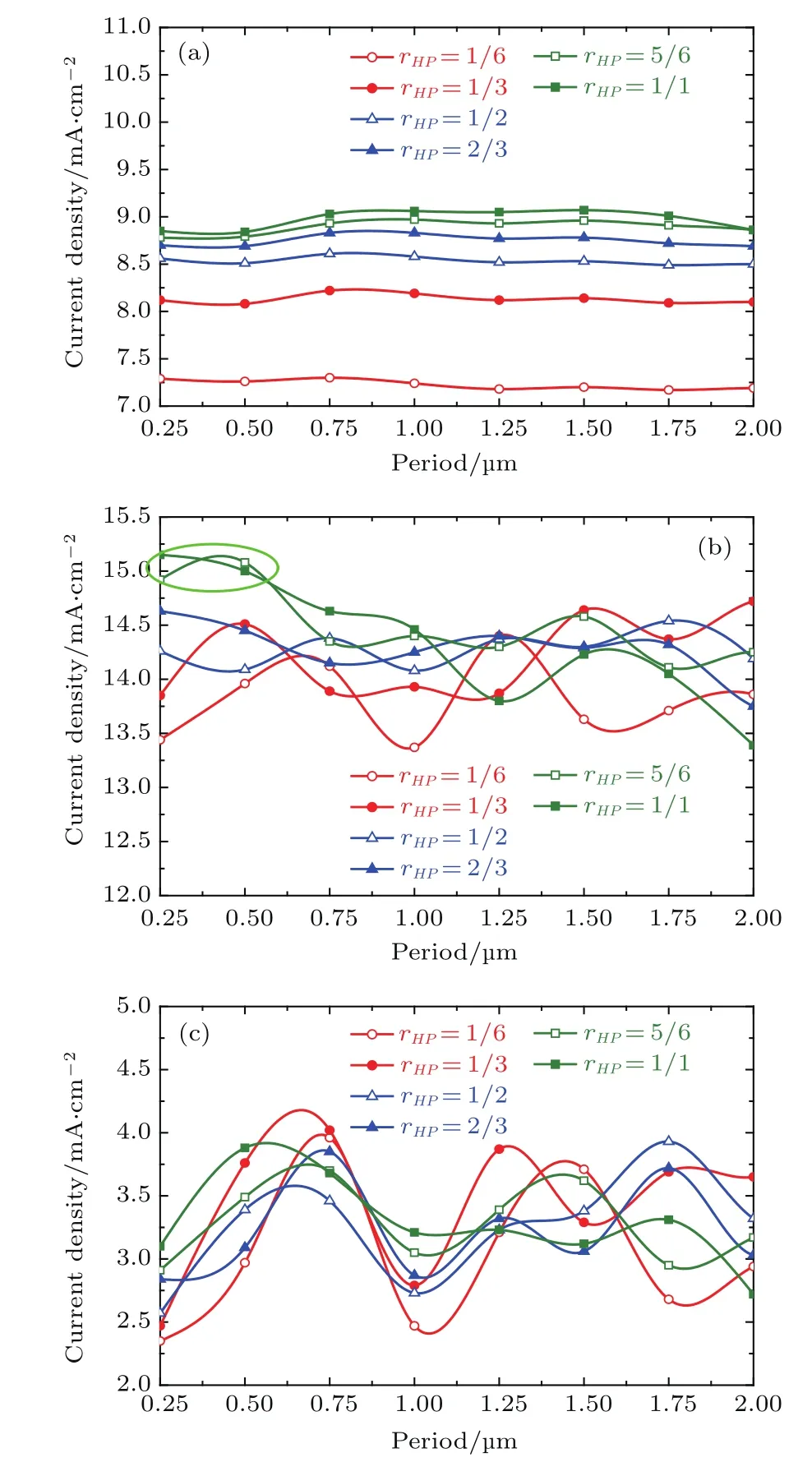
图7 在不同波长范围内周期和纵横比变化对电池本征吸收的影响 (a)300—550 nm;(b)550—800 nm;(c)800—1100 nmFig.7.Effect of period and aspect ratio on the cell intrinsic absorptions in the wavelength range of(a)300–550 nm,(b)550–800 nm,and(c)800–1100 nm.

3.2 占空比对电池各膜层吸收和总吸收的影响

根据前述研究,在占空比为13/15(≈0.87)的条件下,周期和纵横比分别选择0.5µm和1时电池的本征吸收最大化.研究占空比变化对电池总吸收、本征吸收的影响(P=0.5µm,rHP=1),结果如图8所示.从图中可以看出,总吸收和本征吸收随着占空比增大总体呈上升趋势,当占空比接近0.9时吸收达到最大值.

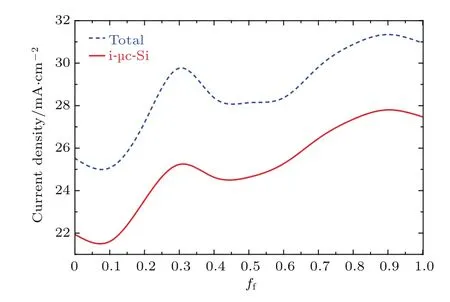
图8 占空比变化对电池总吸收和本征吸收的影响Fig.8.Influence of the fi ll factor on total absorption and intrinsic absorption of the cells.

3.3 周期和占空比不变时继续增大纵横比对电池吸收的影响

在前述研究中发现当P≤1µm时,电池的本征吸收随纵横比的增大而逐渐增大,当rHP=1时吸收实现最大化(0≤rHP≤1),如图5(b)所示.存在一个问题,前述研究中rHP最大值只取到1,那么对于P≤1µm的锥形PC吸收层,继续增大rHP是否会继续提升本征吸收?为此,对周期分别为0.25,0.50,0.75,1.00µm,高度从0增加到2µm时电池本征吸收的变化规律进行研究,如图9所示,对应的rHP分别从0增加到8.0,4.0,2.7,2.0.

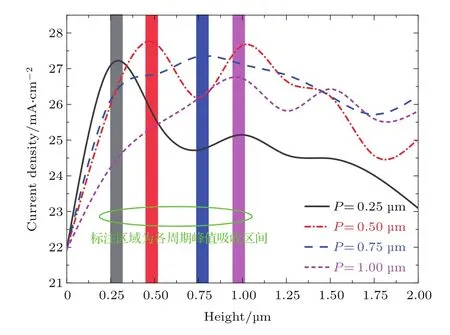
图9 P≤1µm时锥形PC吸收层高度变化(0—2µm)对电池本征吸收的影响Fig.9.Intrinsic absorption versus height of the conical 2D PC(0–2µm)when P ≤ 1µm.

从图9可以看出,随着纵横比的增大,本征吸收先上升而后呈总体下降趋势.当周期分别为0.25,0.50,0.75,1.00µm时,获得本征吸收最大化的对应高度值分别约为0.25,0.50,0.75,1.00µm.由此可以看出,当P≤1µm时,实现本征吸收最大化的rHP均为1,继续增大rHP并不会提升电池本征吸收.

在引言中指出,随机绒面结构可以看作一系列周期性结构经空间傅里叶变换叠加形成.因此在设计优异的随机绒面结构时,重点在于优化绒面形貌的纵横比,当其横向特征尺寸较小时(≤1µm),使其纵横比达到1;而当周期较大时,根据3.1节获得的结论,则应相应减小纵横比.

4 结 论

基于FDTD算法模拟研究了锥形2D PC结构参数对单结微晶硅电池各膜层光学吸收的影响规律.研究表明,引入锥形2D PC吸收层后,电池的本征吸收和寄生吸收都获得提升.寄生吸收主要由ITO引起,本征吸收则随着周期变化呈正弦波动,并且随着纵横比的增大先上升后下降.当周期分别为P≤1.0µm,1.0µm＜P≤1.5µm和1.5µm＜P≤2.0µm时,本征吸收分别在纵横比为1,5/6和1/2时实现最大化,即小周期应采用大纵横比,而大周期应减小纵横比.同时研究发现,为了使更多的光进入电池内部而在电池表面引入绒面减反膜时,重点在于优化绒面形貌的纵横比,使之超过1/2.此外,本征吸收随着占空比增大总体呈上升趋势,当占空比接近0.9时达到最大值.当引入结构参数为P=0.5µm,rHP=1,ff≈0.9的锥形2D PC吸收层时,微晶硅电池短路电流密度从平面结构的21.9 mA/cm2提升到27.8 mA/cm2,相对增加27%.以上结论为实验制备优异的周期或随机绒面陷光形貌提供了重要指导.

[1]Shah A V,Schade H,Vanecek M,Meier J,Vallat-Sauvain E,Wyrsch N,Kroll U,Droz C,Bailat J 2004Prog.Photovoltaics12 113

[2]Moulin E,Bittkau K,Ghosh M,Bugnon G,Stuckelberger M,Meier M,Haug F J,Hupkes J,Ballif C 2016Sol.Energ.Mat.Sol.C145 185

[3]Muller J,Rech B,Springer J,Vanecek M 2004Sol.Energy77 917

[4]Andreani L C,Bozzola A,Kowalczewski P,Liscidini M 2015Sol.Energ.Mat.Sol.C135 78

[5]Isabella O 2013Ph.D.Dissertation(Delft:Delft University of Technology)

[6]Hsu C M,Battaglia C,Pahud C,Ruan Z C,Haug F J,Fan S H,Ballif C,Cui Y 2012Adv.Energy.Mater.2 628

[7]Tan H,Santbergen R,Smets A H M,Zeman M 2012Nano Lett.12 4070

[8]Chen P Z,Hou G F,Fan Q H,Ni J,Zhang J J,Huang Q,Zhang X D,Zhao Y 2015Sol.Energ.Mat.Sol.C143 435

[9]Yan B,Yue G,Sivec L,Owens-Mawson J,Yang J,Guha S 2012Sol.Energ.Mat.Sol.C104 13

[10]Yan B,Yue G,Sivec L,Yang J,Guha S 2011Appl.Phys.Lett.99 113512

[11]Sai H,Matsui T,Matsubara K,Kondo M,Yoshida I 2014IEEE J.Photovolt.4 1349

[12]Sai H,Matsui T,Saito K,Kondo M,Yoshida I 2015Prog.Photovoltaics23 1572

[13]Lin Y Y,Xu Z,Yu D L,Lu L F,Yin M,Tavakoli M M,Chen X Y,Hao Y Y,Fan Z Y,Cui Y X 2016ACS Appl.Mater.Interfaces8 10929

[14]Tanaka Y,Ishizaki K,Zoysa M D,Umeda T,Kawamoto Y,Fujita S,Noda S 2015Prog.Photovoltaics23 1475

[15]Ishizaki K,de Zoysa M,Tanaka Y,Umeda T,Kawamoto Y,Noda S 2015Opt.Express23 1040

[16]Wang Y,Zhang X,Bai L,Huang Q,Wei C,Zhao Y 2012Appl.Phys.Lett.100 263508

[17]Tan H R,Psomadaki E,Isabella O,Fischer M,Babal P,Vasudevan R,Zeman M,Smets A H M 2013Appl.Phys.Lett.103 173905

[18]Tan H,Moulin E,Si F T,Schuttauf J W,Stuckelberger M,Isabella O,Haug F J,Ballif C,Zeman M,Smets A H M 2015Prog.Photovoltaics23 949

[19]Sai H,Saito K,Kondo M 2013IEEE J.Photovolt.3 5

[20]Moulin E,Steltenpool M,Boccard M,Garcia L,Bugnon G,Stuckelberger M,Feuser E,Niesen B,van Erven R,Schuttauf J W 2014IEEE J.Photovolt.4 1177

[21]Dewan R,Shrestha S,Jovanov V,Hupkes J,Bittkau K,Knipp D 2015Sol.Energ.Mat.Sol.C143 183

[22]Soh H J,Yoo J,Kim D 2012Sol.Energy86 2095

[23]Kawamoto Y,Tanaka Y,Ishizaki K,de Zoysa M,Asano T,Noda S 2015Opt.Express23 896

[24]Kawamoto Y,Tanaka Y,Ishizaki K,de Zoysa M,Asano T,Noda S 2014IEEE J.Photovolt.6 4700110

[25]Gomard G,Peretti R,Callard S,Meng X,Artinyan R,Deschamps T,Roca I,Cabarrocas P,Drouard E,Seassal C 2014Appl.Phys.Lett.104 051119

[26]Tamang A,Sai H,Jovanov V,Hossain M I,Matsubara K,Knipp D 2016Prog.Photovoltaics24 379

[27]Shi Y,Wang X,Liu W,Yang T,Ma J,Yang F 2014Opt.Express22 20473

[28]Fisker C,Pedersen T G 2013Opt.Express21 208

[29]Chen P Z,Hou G F,Zhang J J,Zhang X D,Zhao Y 2014J.Appl.Phys.116 064508

[30]Curtin B,Biswas R,Dalal V 2009Appl.Phys.Lett.95 231102