考虑剪切作用的梁元几何非线性损伤分析

2018-08-10詹润涛马文强

信阳师范学院学报（自然科学版） 2018年3期

关键词：泊松比端点弯矩

詹润涛, 冯波，马文强

(信阳师范学院建筑与土木工程学院, 河南信阳 464000)

0 引言

对于桥梁、钢结构等稳定性问题突出的结构,材料的本构关系满足线性关系，但是如果结构构件发生了比较大的平动或转动位移，那么这时就需要分析结构的几何非线性问题.

在结构的几何非线性分析中，材料一般假设为无缺陷的材料,然而结构在制造、安装中，结构的材料会形成缺陷，或者在长期荷载作用下材料性能会发生疲劳退化，这时就需要同时考虑材料性能退化的几何非线性损伤问题.

ALTENBACH等[1]提出一种唯像的本构模型，模拟金属薄壁壳和板的蠕变和损伤过程，通过考虑应变位移关系的二阶项分析了在弯曲情况下的板壳的几何非线性损伤情况.傅衣铭等[2]基于 Talreja 张量内变量损伤模型，建立了具初始挠度的考虑损伤效应的复合材料单层板的非线性压屈平衡方程，应用有限差分法和迭代法进行求解.

这些文献对于分析考虑损伤的结构的几何非线性力学性能做出了有价值的贡献.然而，上述文献主要是分析板问题的几何非线性损伤问题，关于梁的几何非线性损伤问题，相关文献比较少.对于桥梁结构而言，梁结构是主要的受力部件之一，因而分析梁的几何非线性损伤问题具有现实意义.

在外界荷载作用下，材料的性能会发生退化，从而导致弹性模量降低，然而继续承受荷载后，结构的应力应变关系在一些情况下仍旧保持线性，并且发生大位移或大转角，这样采用几何非线性耦合材料非线性的分析方法就不符合实际情况，因为材料非线性分析假设应力应变关系是非线性关系，与实际的材料的线性应力应变关系不相符，因此采用几何非线性耦合弹性损伤力学的方法是一种比较合理的解决方法.

本文引入相关文献弹性损伤力学的概念，分析了考虑剪切作用的梁的几何非线性问题，采用更新Lagrange法(U.L法)编程计算出梁损伤前后几何非线性的荷载位移曲线，对于研究桥梁结构损伤前后的几何非线性问题具有一定参考作用.

1 梁单元几何非线性刚度阵

当梁的高跨比比较大时，需要考虑剪切变形对梁变形的影响，也就是泊松比对梁的受力影响.其计算简图如图1所示.

梁的几何非线性分析有限元方法一般采用总体Lagrangian法(T.L法)和更新Lagrangian法(U.L法).对于采用Von-Karman大挠度理论对梁、板、壳的大挠度、小转动进行T.L法和U.L法几何非线性分析，都可以得到正确解，而在大挠度、大转动的情况下，须采用U.L法才能得到正确解[3].尤其对于桥梁结构中，U.L法得到了广泛的应用[4].本文采用U.L法进行几何非线性分析(见图2).U.L法的单元刚度阵为:

k=k0+kσ,

(1)

其中k是梁单元刚度阵，k0是线弹性刚度矩阵，kσ是初应力刚度阵[5].

对于考虑剪切作用的梁的线弹性刚度阵k0如式(2)所示[6].

[k0]=

(2)

参数b=12EI/(GAL2),剪切形状系数取=6/5，其中E、A、I、L、G分别是弹性模量、横截面积、惯性矩、长度、剪切模量.

[kσ]=

(3)

采用文献[6]流动坐标计算杆端位移和杆端力.

图1 梁的计算模型Fig. 1 Computation model for beam

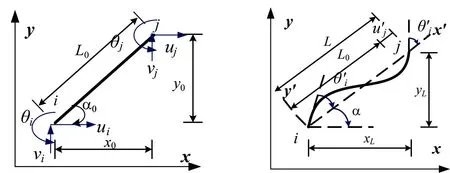
(a) 变形前的梁单元 (b)变形后的梁单元

流动坐标x′y′下的单元的长度变化为：

(4)

在流动坐标x′y′下的单元结点位移：

α=arctan(yL/xL),

(5)

(6)

(7)

{Fe′}=[ke′]{de′},

(8)

其中[ke′]为局部坐标系的单元阵，按照式(1)计算.转换矩阵如式(9)所示.

相关几何非线性有限元分析具体的流程在本文第3节详细论述.

[T]=

(9)

(10)

{Fe}=[ke]{de′}.

(11)

2 损伤变量和损伤演化方程

2.1 损伤变量

(12)

参考式(12)定义四阶损伤张量：

(13)

式(13)可变化为：

(14)

各向同性线弹性体弹性张量[9]:

Cijkl=λδijδkl+G(δikδjl+δilδjk),

(15)

(C0)ijkl=λ0δijδkl+G0(δikδjl+δilδjk),

(16)

Dijkl=αδijδkl+β(δikδjl+δilδjk).

(17)

根据张量的定义，式(17)可变化为:

Cijrs=(C0)ijrs-Dijkl(C0)klrs,

(18)

将式(15)、(16)、(17)代入式(18)可得：

λδijδrs+G(δirδjs+δisδjr)=

λ0δijδrs+G0(δirδjs+δisδjr)-

(αδijδkl+β(δikδjl+δilδjk))(λ0δklδrs+

G0(δkrδls+δksδlr)).

(19)

利用δikδjlδkl=δij，δklδkl=3，δrlδls=δrs，式(19)展开为

(λ-λ0-3αλ0-2αG0-2βλ0)δijδrs+

(G-G0(1-2β))(δirδjs+δisδjr)=0,

(20)

可得Lame常数λ,G和损伤变量α,β的关系:

λ=λ0-3αλ0-2αG0-2βλ0,

(21)

G=G0(1-2β).

(22)

将λ=(3K-2G)/3代入式(21)，可得体积模量K和α、β的关系式：

K=K0-K0(3α+2β).

(23)

令

3α+2β=ξ,

(24)

式(24)变化为:

K=K0(1-ξ).

(25)

利用式(26)和式(27),式(22)和式(25)变为式(28)和式(29)[9]:

(26)

(27)

(28)

(29)

文献[7]没有给出损伤前后的弹性模量和泊松比的显式表达式，本文用式(28)和式(29)求得损伤前后弹性模量和泊松比的显式表达式(30)和(31),从而可以直接对U.L法中梁刚度阵的E、ν进行更新：

(30)

(31)

2.2 损伤演化方程

由式(30)和式(31)可以看出，损伤前后E0,ν0和E,ν的关系由损伤变量ξ,β决定，只要知道ξ,β的损伤演化方程，就可以知道损伤前后弹性模量和泊松比的变化情况.一般采用自由能函数或者应变能函数作为损伤演化函数，例如文献[7]采用的是以应变能作为损伤演化函数.

对于只考虑承受弯矩、轴力、剪力的梁的应变能式为：

(32)

其中：M、N、Q分别是弯矩、轴力、剪力.

通过编制几何非线性损伤程序，发现利用应变能作为损伤演化函数进行相关计算比较困难，如图1所示，如果悬臂梁作用竖向力Fy或者工程中高桩作用水平荷载，对于悬臂梁或者高桩的几何非线性问题，每次荷载迭代计算梁单元的M、N、Q对于单元的两个节点不是一对平衡力，一端有弯矩，另一端没弯矩，或者两端的弯矩不相等，如图3所示.因此无论采用梁的节点1还是节点2的M、N、Q计算应变能不能反应梁单元的应变能，尤其当M特别大时，弯矩对应变能的计算影响特别大.如果采用式(32)积分方法计算应变能对于U.L列式又是比较难以计算，因为U.L的有限元列阵提供的是梁单元两端的节点力，单元中间位置节点力没有提供，同时梁单元会发生变形，长度会发生变化，损伤前后弹性模量会发生变化，这也会增加计算应变能的难度.

图3 梁单元节点力Fig. 3 Node force of beam element

由于悬臂梁中的最大位移发生在端点2，为了简化计算,将端点2的位移函数作为损伤演化函数，从而建立损伤演化方程.设梁单元的位移为u,v,θ，利用量纲分析可知，式(32)应变能W量纲为[质量][长度]2/[时间]2,因此在不考虑质量和时间的情况下，也就是在质量均匀和不考虑荷载速率的情况下，采用位移的二次方的形式和应变能是等价的.为保持量纲的一致性，对照式(32)定义无量纲损伤演化函数Φ为：

Φ=u2/A+v2/A+θ2.

(33)

当单元划分较小时，梁单元两端位移差别较小，采用位移模式作为损伤演化函数可以克服应变能作为损伤演化函数带来的计算困难，也能够反映几何非线性分析中大位移和大转角对材料损伤的影响；位移函数相对应变能、自由能来说，更加可测，在一定程度上克服自由能和应变能作为损伤演化函数的唯象性的缺陷(自由能和应变能比较难以测量).

参考文献[7]，定义损伤演化方程为:

(34)

(35)

其中：m、n、c1、c2是系数；Φt是损伤的阀值，即位移函数大于Φt，损伤开始发生；Δt代表荷载步的变化，例如当荷载步为等值变化[0,a,2a,3a,…]，这时t=(2a-a)/(a-0)=1.损伤变量增量形式：

(36)

(37)

3 几何非线性损伤程序流程图

参考文献[3,6,7,10]和本文第1,2节的相关式，编制几何非线性损伤Matlab程序，迭代收敛条件:

(38)

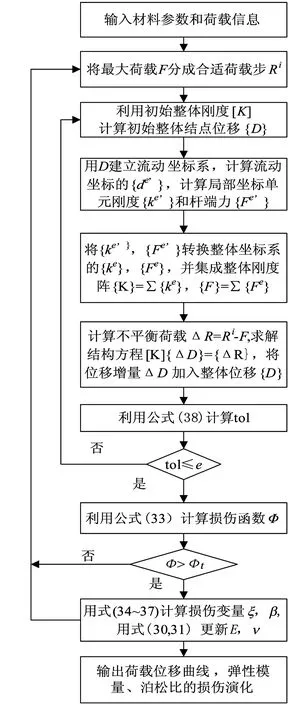
图4 梁的几何非线性损伤程序流程图Fig. 4 Flow chart of geometrically nonlineardamage mechanics analysis for beam

4 算例

如图1，根据热轧型钢规范[11]，采用工字梁型号30b，参数为：E=210 GPa，ν=0.3，梁宽B=128 mm，梁高H=300 mm，面积A=67.254 cm2,惯性矩I=9400 cm4，长度L=3.0 m，设受力为受压为主，Fx=1500 kN，Fy=150 kN,c1=c2=0.005,m=n=2.屈曲荷P=5 406.247 kN，Fx小于P，因此梁没有屈曲失稳.

为了验证编制的Matlab程序的正确性，首先利用Ansys 12分别对图1进行线弹性和几何非线性分析，也就是在APDL语言中分别设NLGEOM OFF和NLGEOM ON，采用beam4单元，端点2的位移列于表1.然后采用U.L列式编制Matlab程序.

为了简化分析，将图1划分为一个单元进行编程计算，X、Y方向的分步加载，每次荷载增量分别为150 kN和15 kN，计算可得梁端点2的几何非线性的位移列于表1.本文分析两种考虑损伤的工况，

(1)当损伤演化函数超过阀值，损伤发生，损伤阀值参考式(33),定义如下：

Φt=(u)2/A+(v)2/A+(θ)2=0.70.

(39)

(2)取Φt=0.01时，损伤开始发生.

几何非线性和几何非线性损伤两种情况下，Matlab程序计算的梁端点2的位移最大值列入表1.通过表1可以看出，利用Matlab程序计算的梁端2的几何非线性位移与用Ansys 12的划分10个单元计算的几何非线性位移相差不大，但是与Ansys 12线弹性计算的梁端点2的位移相差比较大，说明编制的几何非线性程序是正确的.当Φt=0.7时表明，此种工况下计算端点2的几何非线性位移与考虑损伤的几何非线性位移差别不大，当Φt=0.01时，即几乎初始加载后损伤就立刻发生，此时端点2的位移的增加量比较大，说明按照式(34)和式(35)计算，荷载位移曲线对损伤的发生时刻是比较敏感的.

图5表示不同荷载步的端点2的考虑损伤和未考虑损伤的几何非线性荷载位移曲线，程序每个荷载步按照图1坐标系统计算,所得的位移为负值，将其取绝对值，从而得到图5荷载位移曲线.

由于当Φt=0.7时，如表1所示，考虑和未考虑损伤计算的位移相差不大，因此图5采用工况为Φt=0.01的荷载位移曲线.

由于c1=c2,m=n，损伤变量β，ξ的损伤演化规律相同.将程序计算的弹性模量和泊松比除以初始弹性模量和泊松比进行归一化处理.图6表示损伤变量β，ξ和弹性模量、泊松比的损伤演化曲线，如图6所示，损伤变量β,ξ和弹性模量、泊松比在荷载1200 kN之前的损伤演化比较平稳，但是超过1200 kN之后，损伤开始加快发展，表明损伤演化具有非平稳变化特点.