BaLiF3晶体的弹性及热力学性质研究
2018-08-10陈善俊张伟斌程书博韦建军
陈善俊,魏 敏,陈 艳,张伟斌,3,程书博,韦建军
(1.长江大学 物理与光电工程学院,湖北 荆州 434023;2.四川大学 原子与分子物理研究所,四川 成都 610065;3.东国大学 物理系,首尔 04620)
0 引言
BaLiF3晶体是一种立方型钙钛矿结构的复合氟化物晶体,具有独特的结构与良好光学特性:折射率较低、光学透明度较高.因此,在工业应用领域,它可作为光存储激励、能量转换、新型激光等重要材料,并在基础领域研究和技术领域研究占有举足轻重的地位.近年来,随着研究的深入,它引起了科研工作者的广泛关注.实验研究方面:BOUMRICHE[1]等人采用XRD确定BaLiF3晶体为立方的钙钛矿结构,测得其晶格常数为0.3996 nm.BESNALAH[2]等人在CF4气氛下制备出了BaLiF3单晶体,并测得吸收峰在123 nm(10.1 eV)处.LIN[3]等人制备了含BaLiF3纳米晶体的新型氟氧
化物玻璃陶瓷(GCs),其尺寸在30 nm左右.石春山[4,5]等人采用高温固相法在Ar气流中制备得到BaLiF3微晶粉末,并对其抗辐照损伤特性进行了探索性研究,发现X射线对其产生的损伤一般很容易恢复.MISHRA[6]等人采用高压X射线衍射,研究了钙钛矿结构的BaLiF3晶体在0~50 GPa条件下的稳定性,并得到其体弹模量为75.9 GPa.QIANG[7]等人通过X射线衍射(XRD),确定了BaLiF3的晶体结构,并首次研究了在980 nm激发下新型Er3+/Ho3+、Yb3+共掺杂BaLiF3微晶的上转换发光特性.理论计算方面:NISHIMATS[8]等人采用第一性原理方法,研究了掺杂后的BaLiF3晶体的能态密度及能带结构,重点研究了Cr2+、Mn2+等二价过度金属离子对BaLiF3的能带结构影响规律.YALCIN[9]等人采用第一性原理计算方法,从理论上研究了BaLiF3、BaLiH3和SrLiH3钙钛矿材料的结构、力学、电子、光学和动力学性质,并指出BaLiF3是一种有潜力的激光候选材料.
目前关于BaLiF3晶体的实验和理论研究主要集中在BaLiF3晶体光学性质方面,而关于它的热力学性质的研究比较少,特别是在极端条件(高温高压)下的热力学性质研究尚显不足.为此有必要研究其在高温高压下的热力学性质,为BaLiF3晶体在极端条件(高温高压)下的应用研究提供理论指导.
本文采用第一性原理超软赝势平面波密度泛函理论(DFT)[10-12]的方法,研究钙钛矿结构BaLiF3晶体的弹性及热力学性质,进而研究压强和温度对其热力学性质的影响规律,使得BaLiF3晶体的特征和性质在理论上更加全面地显示出来,为BaLiF3晶体的制备及其在热力学应用方面提供理论指导.
1 理论计算方法
本文计算运用的是第一性原理平面波赝势方法——CASTEP程序包[13],釆用BFGS[14]算法对晶胞进行几何结构优化,交换关联能采用广义梯度近似(The Generalized Gradient Approximation, GGA)[15]的PBEsol形式.原子势采用超软赝势,平面波截断能量为850 eV,k点网格取12×12×12.在迭代过程中,能量自洽收敛在5.0×10-6eV/atom、最大力收敛标准为0.1 eV/nm、最大位移收敛标准为5.0×10-5nm.
BaLiF3晶体为立方钙钛矿结构,其空间群为Pm-3m.每个BaLiF3晶胞中含有5个原子,Li原子占据晶胞体心,而Ba原子位于立方体顶角位置,F原子位于面心.相应的原子坐标分别为Ba(0.0, 0.0, 0.0)、Li(0.5, 0.5, 0.5)、F(0.5, 0.5, 0.0),其原子空间排布如图1所示.
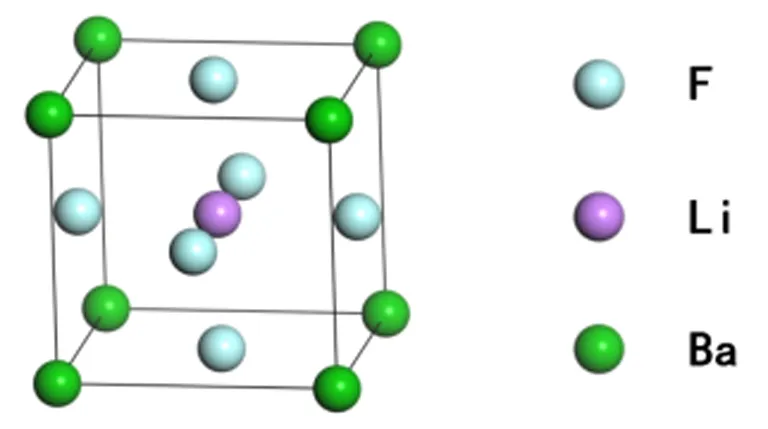
图1 BaLiF3的晶体结构模型Fig. 1 Unit cell structure of BaLiF3
为了研究BaLiF3晶体热力学性质,本文采用准谐德拜模型[16].在该模型中,BaLiF3晶体的非平衡Gibbs函数G*(V;p,T)可表示为:
G*(V;p,T)=
E(V)+pV+Avib(Θ(V);T).
(1)
在式(1)中:等式右边第一项E(V)为每个BaLiF3原胞的总能量,第三项AVib为Helmholtz振动自由能,Θ(V)为德拜温度.在准谐德拜模型中,AVib可表示为[17,18]:
3ln(1-e-Θ/T)-D(Θ/T)).
(2)
在式(2)中:D(Θ/T)为德拜积分,n为单个原胞中总原子数,kB为玻尔兹曼常数.若晶体是各向同性的,则德拜温度Θ可表达为:
(3)
式(3)中:M为原胞的分子质量,σ是泊松比率(Poisson ratio),f(σ)参阅文献[19],Bs为晶体的绝热体弹模量,即有以下形式:
(4)
当p、T一定时,对非平衡Gibbs函数G*(V;p,T)最小化,只需对V求偏导,得到最小值,即:
(5)
通过求解方程式(5),得到晶体原胞的热力学状态方程,进一步可以得到等温弹性模量BT、等体热容Cv、热膨胀系数α,即:
(6)
(7)
(8)
在式(8)中,γ为格林艾森参数,可表示为:
(9)
2 结果与讨论
2.1 BaLiF3的弹性性质
本文采用广义梯度近似GGA-PBEsol对BaLiF3晶体的晶胞进行了几何结构优化,计算了零温、零压下BaLiF3平衡晶格常数,如表1所示.从表1中可以看出,我们计算的BaLiF3的晶格常数为0.3978 nm,仅比实验值0.3996 nm[1]和0.3995 nm[6]略小,与其他的理论值也很接近[20,21].由此表明,在此结构下,计算结果十分可信.
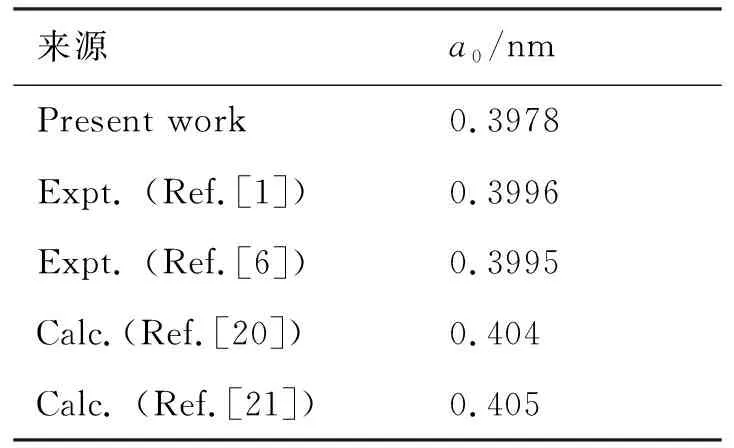
表1 零温零压下的BaLiF3的晶格常数Tab. 1 Lattice constant a0 under 0 GPa and 0 K for BaLiF3
BaLiF3是面心立方结构晶体,对于立方晶体,弹性常数Cij有三个非零独立分量,即C11、C12与C44.体弹模量和剪切模量可由VOGIT[22]、RUESS[23]、HILL[24]近似得到,由VOGIT近似:
(10)
由Ruess近似[23]得,
(11)
根据HILL[24]的理论证明,GV和GR的算术平均值为多晶体模量G,即:
(12)
在压强p=0 GPa条件下,立方晶体的体弹模量与弹性常数存在以下关系:
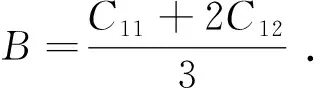
(13)
表2给出了零温零压下的BaLiF3弹性常数、体弹模量和剪切模量.由表2可知,KORBA[21]等计算的弹性常数和体弹模量与实验值[1,6]相比,误差较大.而我们的计算结果与实验值[6]相符较好.由此表明,本文的计算结果是可靠的.
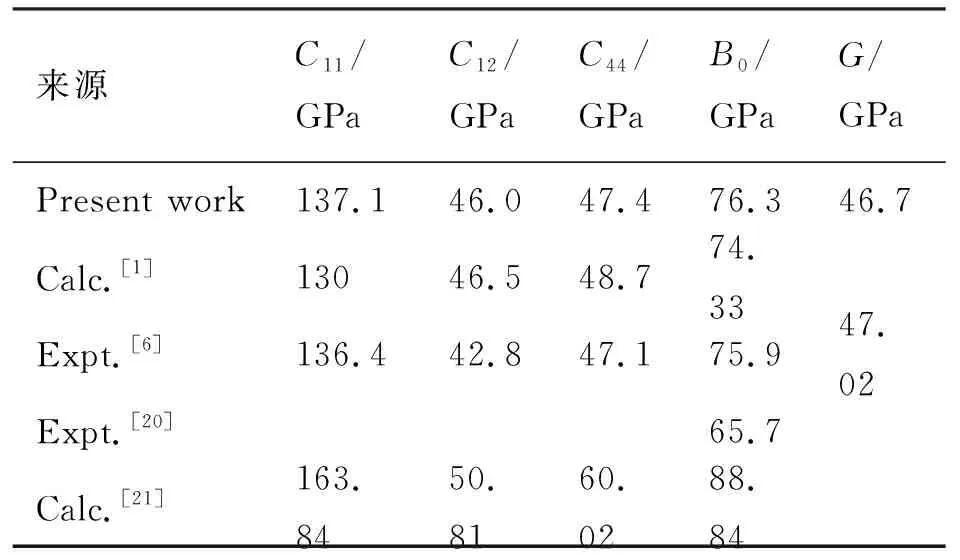
表2 零温零压下的BaLiF3晶体弹性常数Cij、体弹模量B0、剪切模量GTab. 2 Elastic constants Cij、Bulk modulus B0 andshear modulus G under 0 GPa and 0 K for BaLiF3
由PUGH[25]提出的晶体力学行为标准可知:B/G的值越大,晶体的延展性越好,反之晶体延展性越差(易碎),其临界值为1.75.由表2数据计算得到BaLiF3的B/G值为1.64,说明BaLiF3晶体的延展性较差.因此,BaLiF3不易在低压条件下制备.由表2数据可以进一步计算得到不同压强下的B/G值,见表3数据,可以发现B/G值在相变范围内随着压强的增加而增大,表明BaLiF3在高压条件下更易制备.
根据立方晶体的结构稳定性要求,弹性常数需同时满足以下三个条件:
C44-p>0,
C11-C12-2p>0 ,
(14)
C11+2C12+p>0.
表3给出了压强在0~190 GPa范围内,温度T=0 K时,BaLiF3晶体的弹性常数、体弹模量和剪切模量.
图2给出BaLiF3弹性参数随压强的变化关系.由表3和图2可知,弹性常数C11、C12和弹性模量B随着压强的增加有着近似线性的增长,而C44增加相对缓慢.根据立方晶体结构稳定性要求,由表3数据计算可得,当压强p<186 GPa时,BaLiF3晶体的力学结构是稳定的.当压强p>186 GPa时,弹性常数不能完全满足立方晶体结构稳定性的判据,因此BaLiF3晶体失去力学结构稳定性,此时钙钛矿结构不能维持.如果此时继续增大压强,BaLiF3晶体就极有可能发生相变.但目前并没有相关实验结果与之佐证.
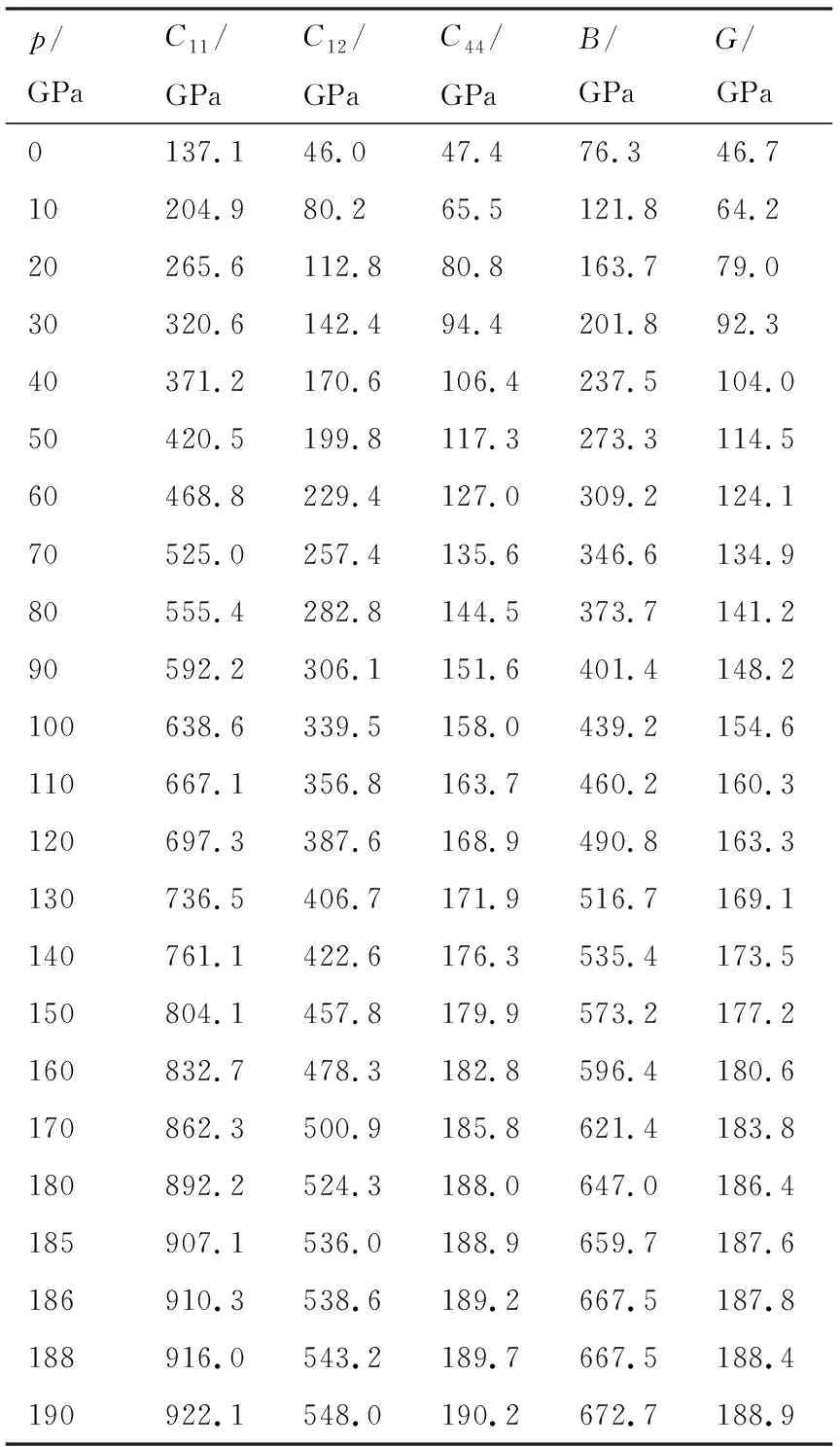
表3 T=0 K时不同压强下BaLiF3的弹性常数(Cij)、体弹模量(B)和剪切模量(G)Tab. 3 Elastic constants Cij、bulk modulus B and shearmodulus G under different pressures for BaLiF3 at 0 K
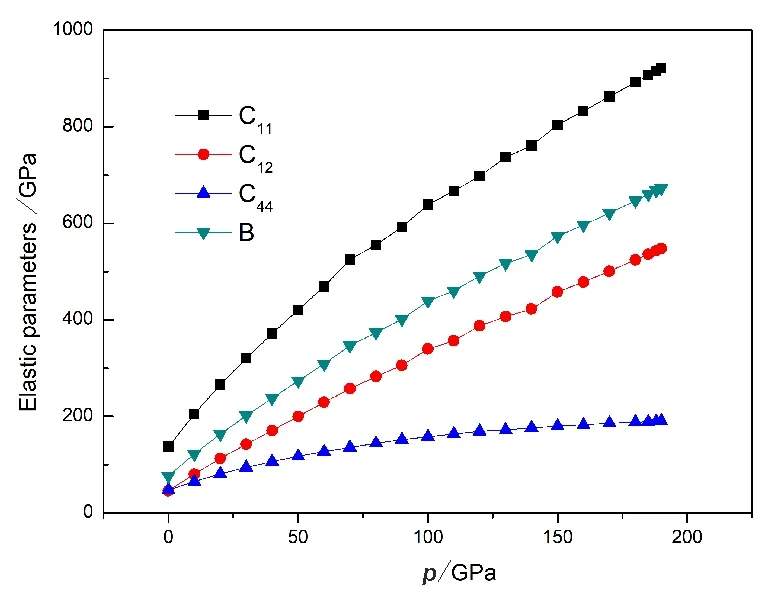
图2 BaLiF3弹性参数和压强的关系Fig. 2 Elastic-related parameters versus pressure of BaLiF3
图3给出了BaLiF3晶体相对体弹模量与温度和压强的关系,其中B为不同温度不同压强下的体弹模量.由图3(a)可知,当0 K
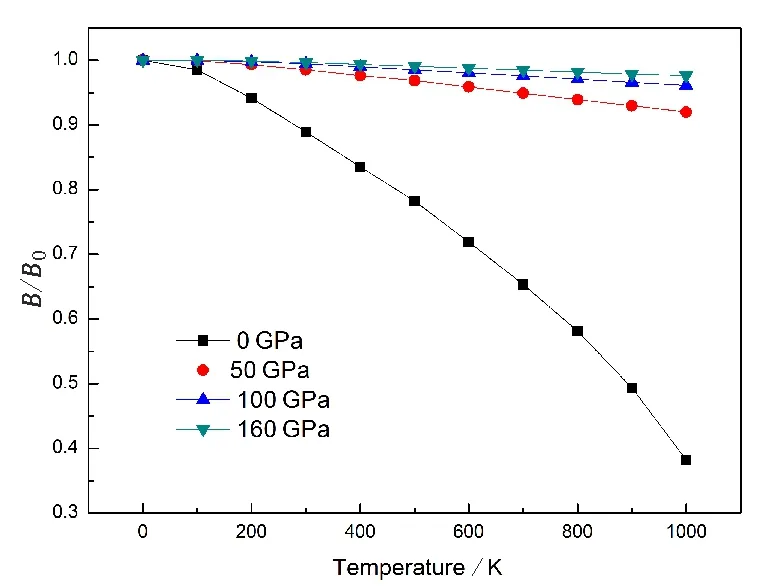
图3(a) BaLiF3晶体的相对体弹模量与温度的关系Fig. 3(a) The variation of relative bulk modulus B/B0as a function of temperature for BaLiF3B0为0 K下的体弹模量
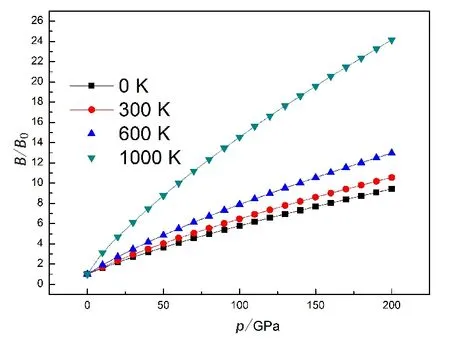
图3(b) BaLiF3晶体的相对体弹模量与压强的关系Fig. 3(b) The variation of relative bulk modulus B/B0as a function of pressure for BaLiF3 B0为0 GPa下的体弹模量
2.2 BaLiF3的热力学性质
为了研究外加压力对BaLiF3晶体结构的影响规律,选取一系列的晶格常数,计算相应的原胞体积V与对应的总能量E,然后把能量和体积用Birch- Murnaghan equation of state(EOS)状态方程进行拟合得到E-V曲线,见图4.前面计算得到BaLiF3晶体的相变压强为186 GPa,所以研究0~200 GPa的热力学性质.根据图4中第一性原理计算得到的E-V曲线的数据用GIBBS程序来完成相关计算.利用GIBBS程序模拟计算得到的晶体热力学数据有一定的误差,但和相应真实数据处在同一个数量级,所以可以用该方法从理论上预测相关的热力学性能,为实验研究提供理论指导.
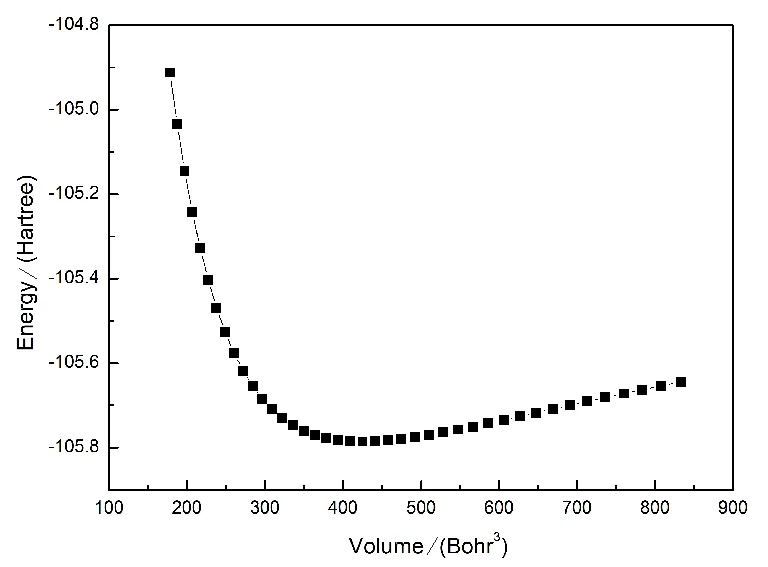
图4 BaLiF3总能量(E)和原胞体积(V0)的关系Fig. 4 Total energy(E) versus unit cellvolume(V0) of BaLiF3
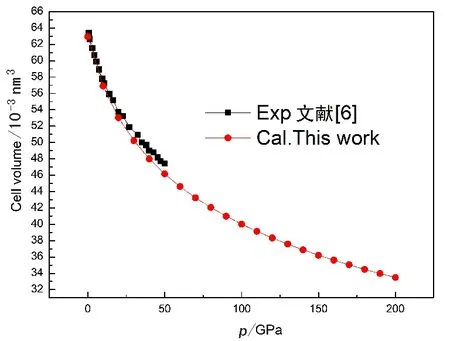
图5 BaLiF3晶体体积与压强的关系Fig. 5 The variation of cell volume of withpressure for BaLiF3
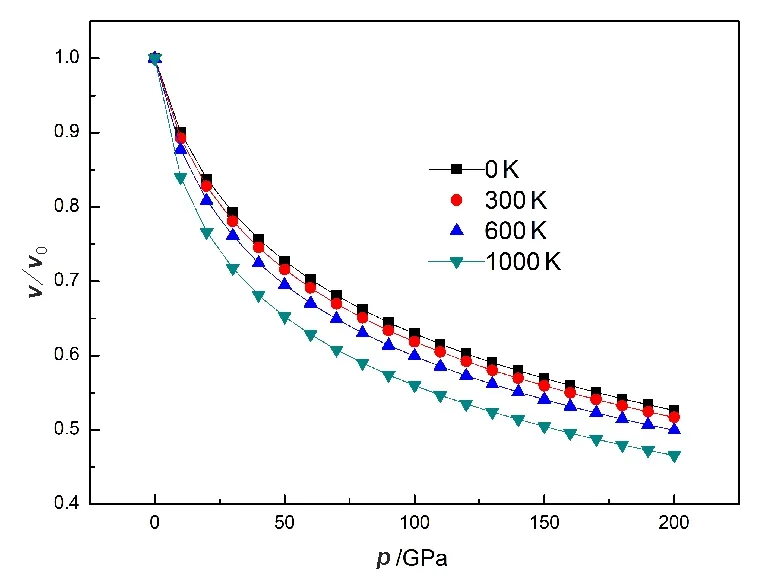
图6 不同温度下BaLiF3晶体相对体积与压强的关系Fig. 6 The variation of relative volume V/V0 as afunction of pressure at different temperature for BaLiF3
实验上,MISHRA[6]等选取了在0~50 GPa之间一系列的压强,测量了BaLiF3原胞体积.图5为BaLiF3晶体体积随压强的变化关系,其中包括,我们的计算结果(0~200 GPa)与实验值[6]的比较.由图5中两条曲线走向的比较,可以清晰地看到,我们计算的理论值与实验值相符较好,尤其是当压强较小时(p<25 GPa),两条曲线几乎是完全吻合的.在p>25 GPa时,我们的计算结果略低于实验值,但也是在合理的误差范围之内.图6给出不同温度下BaLiF3晶体相对体积与压强的关系,其中V0为零压下平衡体积.由图6可知,在一定温度下,压强增加相对体积减小;在一定压强下,温度越高相对体积越小,即高温下的曲线下降得更快.这是由于高温固体更容易被压缩,高温下粒子能量增加,热运动加剧,固体更容易被压缩.
图7为不同压强下等体热容Cv与温度T的关系,图8为不同压强下等压热容Cp与温度T的关系.
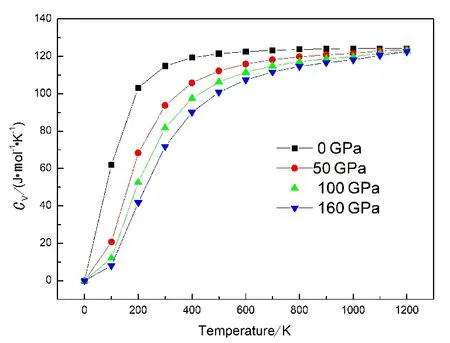
图7 不同压强下BaLiF3晶体等体热容与温度的关系Fig. 7 Constant volume heat capacity as a functionof temperature at different pressure for BaLiF3
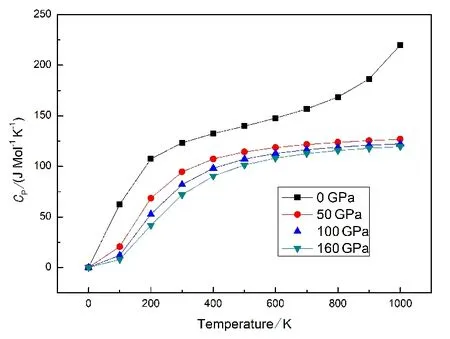
图8 不同压强下BaLiF3晶体等压热容与温度的关系Fig. 8 Constant pressure heat capacity as a functionof temperature at different pressure for BaLiF3
从图7、图8中知,在相同的温度下,等体热容和等压热容随着压强的增大而减小;一定压强下,在相对低温中(T<900 K),等体热容和等压热容随着温度的增加而增大,在相对高温中(T>900 K),等压热容随着温度的增加依然有着一定程度的增大,但较高的温度中,随着温度的增加,等体热容接近Dulong-Petit极限.在T<900 K时,等体热容随温度变化显著,因为在此范围内BaLiF3体积的变化较为明显;当T>900 K时,温度增加等体热容增幅很小近乎为零,这是由于晶体非谐效应(高阶项)的影响,等体热容接近Dulong-Petit极限3nNAkb(NA为阿伏加德罗常数).对于BaLiF3晶体,n=5,即约为124.75 J·mol-1·K-1.
热膨胀系数α能够直观地反映物质的结构稳定性.因为在简谐近似中, 原子间相互作用势能曲线的形式是对称的抛物线,因此不会有热膨胀现象的发生.又因为准谐德拜模型考虑了非简谐效应,晶体的热膨胀系数α及格林艾森参数γ(见式(9))才不为零.图9为压强p在50、100、160 GPa时BaLiF3晶体热膨胀系数与温度的关系.由图9可知,相同压强下,在相对低温中(T<500 K),随着温度的升高热膨胀系数迅速增大,在相对高温中(T>500 K),温度增加热膨胀系数变化较小,尤其是在高温时热膨胀系数随着温度的增加而近乎不变,这表明BaLiF3晶体在经过初期明显的体积膨胀后,在高温中具有良好的体积不变性;在一定温度下,压强越大,热膨胀系数越小,这说明高压下BaLiF3有较好的体积不变性.
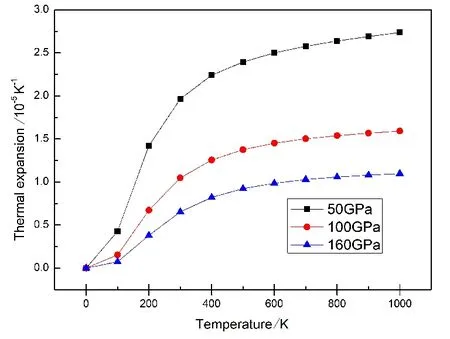
图9 不同压强下BaLiF3晶体热膨胀系数与温度的关系Fig. 9 The variation of the thermal expansioncoefficient α as a function of temperatures atdifferent pressures for BaLiF3
图10给出了温度在300 K、600 K、1000 K时,相对德拜温度和相对热容与压强的关系.由图2和图10可知,德拜温度与体弹模量存在比例关系,压缩性的增大导致了德拜温度的减小,硬质材料有着更高的德拜温度.压强一定时,温度越高,相对德拜温度越高,相对热容越大;当温度恒定时,相对德拜温度随压强增加而增大,而相对热容随压强增大而减小.这是因为增大压强和降低温度的效应是相同的,但是相比于温度对德拜温度的影响,压强对其影响更大.通过准德拜模型,本文计算常温(T=300 K)下,BaLiF3晶体的德拜温度Θ为389.06 K,目前还未有实验值与之比较.
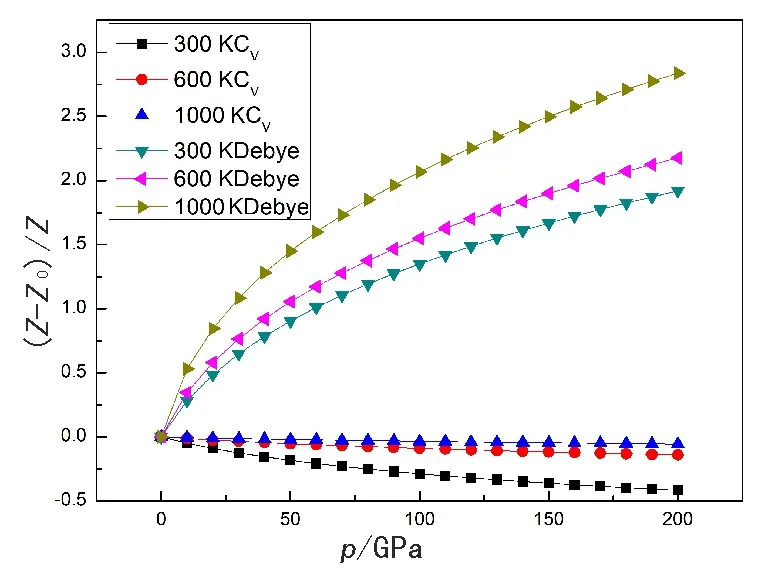
图10 BaLiF3的相对德拜温度和相对热容与压强的关系Fig. 10 The relative Debye temperature and relativeconstantvolume heat capacity at various pressureas a function of pressure for BaLiF3
Z为各压强下的德拜温度和热容,
Z0为p=0时的德拜温度和热容
3 结论
利用基于平面波赝势密度泛函理论的第一性原理,并结合准德拜模型,研究了温度和压强对BaLiF3晶体弹性性质和热力学性质的影响.所计算的BaLiF3晶格常数、弹性常数、体弹模量、剪切模量与实验值及其他计算理论值都符合得很好.得到BaLiF3的B/G值为1.64(小于1.75),说明它是脆性的.依据立方晶体力学稳定条件得到其相变点为186 GPa.通过准谐德拜模型,得到常温下德拜温度Θ为389.06 K.热容随压强升高而降低,在高温下热容接近于Dulong-Petit极限.
