一种基于自适应粘滞Landweber算法的雷达杂波模拟方法

薛永生，高玉章

（1.海军装备部飞机办公室，北京100071，2.海军航空大学青岛校区，山东青岛266041）

雷达杂波是建立与实际雷达工作环境相一致模型的重要组成部分[1]。在低仰角或高分辨率雷达情况下，Weibull分布模型可以在很宽的条件范围内很好地与实验数据相匹配[2]。目前，使用无记忆非线性变换法（ZMNL）[3-4]进行Weibull杂波模拟的关键之处，在于确定非线性变换前后相关系数的关系[5]。为了快速地求解相关的非线性函数，目前常用迭代的方法来代替查表、分段近似[6]、多项式拟合[7]等方法。但是当前的迭代方法[8]多为隐格式迭代法，收敛速度较慢，且在实际应用时需要更多的初始条件。因此，有必要变换问题的求解角度，引入高效的非线性迭代算法来解决这一问题。

第一类算子方程问题是最优化理论中的一个重要问题，在信号处理和图像重建等领域有着广泛的应用[9-10]。传统的Landweber算法虽然可以用来进行逼近第一类算子方程问题的数值解，但由于收敛速度慢，提出了一些改进的方案，如预处理方法[11]、最大期望法[12]、时变步长法[13]、一维搜索法[14]等。但均未见在迭代结构和自适应步长方面有系统的优化。

本文针对Landweber算法[11]，提出了一种具备粘滞迭代格式和自适应步长的迭代算法，并将ZMNL方法中相关系数非线性关系的求解转化为第一类算子方程问题。利用给定分布的相关函数和所提出的显格式迭代算法对相关高斯分布的相关系数进行了求解。计算机仿真结果表明，该算法与以往的隐函数迭代算法相比较，能够在有效地提高杂波的模拟精度的同时，明显地减少迭代的次数。

1 相关Weibull分布雷达杂波产生模型

1.1 无记忆非线性变换法

无记忆非线性变换法原理如图1所示。

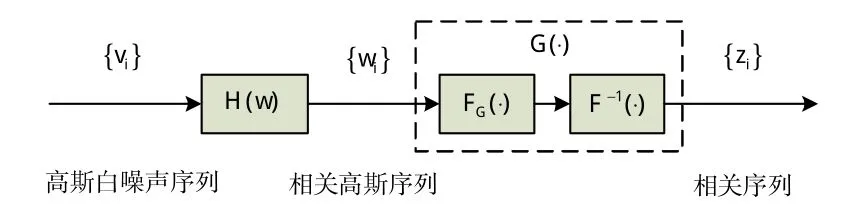
图1 ZMNL法原理图Fig.1 Diagram of ZMNL schematic

基本思想[8]是，高斯随机序列{vi}线性变换后得到{wi}，{wi}仍服从高斯分布。FG(⋅)与F-1(⋅)联合构成非线性变换G(⋅)，FG(⋅)对于服从高斯分布序列的随机值求其分布函数，得到0、1之间的均匀分布序列，这样零记忆非线性变换后得到的{zi}为相关Weibull分布随机序列。序列{zi}的自相关函数S与序列{wi}的自相关函数ρ必然存在非线性关系。只要已知S就可以求得ρ，进而可以谱分解得到H(w)。

1.2 相关Weibull分布杂波模型

Weibull分布[15]模型能很好地描述地杂波、海杂波，其概率密度函数可表示为：

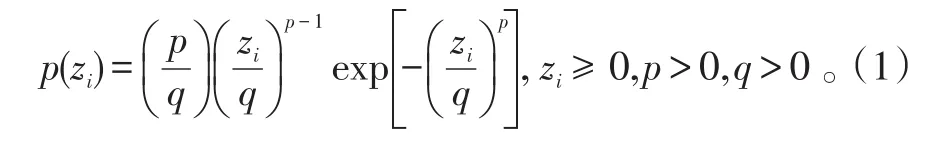
式（1）中：q是表征尺度的参数；p是控制分布尾部形状的参数。

Weibull分布随机变量z可以用2个正态分布随机变量w1和w2表示，即非线性变换

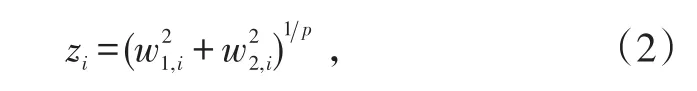
式中，w1,i和w2,i（i=1,2,…）相互独立且满足同一正态分布N(0,σ2)，并且有q=(2σ2)1/p。

Weibull分布的产生框图[16]，如图2所示。

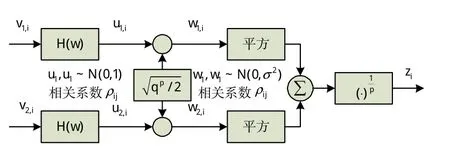
图2 Weibull分布产生原理图Fig.2 Diagram of Weibull distribution produces schematic

相关系数Sij与正态分布相关系数ρij的关系[17]：

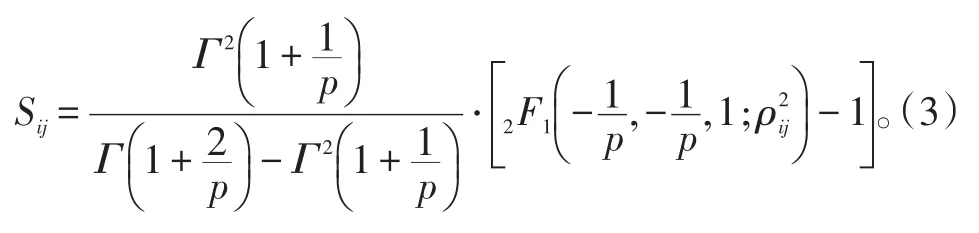
式（3）中：Γ为Gamma函数；2F为高斯超几何分布函数。

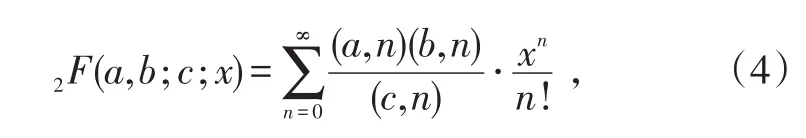
式中，(a,n)=a(a+1)(a+2)…(a+n-1)，当n=0 时，(a,0)=1，a≠0。

2 基于自适应粘滞Landweber算法的杂波模拟方法

在给定所需产生的Weibull杂波的情况下，需要根据杂波的相关函数Sij得到相关高斯序列的相关系数ρij，由于式（3）中用到高斯超几何函数和伽玛函数这些特殊函数，所以无法直接求得相应的ρ显示封闭解。本文以一种具备粘滞迭代格式和自适应步长的Landweber改进算法给出S到ρ的显示迭代格式。

2.1 自适应粘滞Landweber算法

设C={P∈ℝM}和Q={b|b∈ℝM}分别是Hilbert空间H1和H2中的非空闭凸子集，A:C→Q为有界线性算子，寻找满足下面第一类算子方程条件的x，

可用Landweber迭代算法[11]求解。

Landweber算法。设x0是任意的，且n=0,1…,计算：

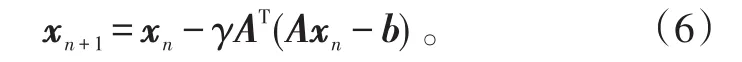
式（6）中：A为M×N实矩阵；γ∈(0,2/L)，L为矩阵ATA的最大特征值‖x*-x‖。

为逼近最优解，可令式（6）的停止规则为：

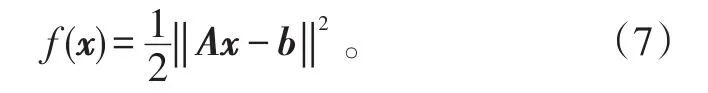
式（7）为最小约束问题，因而Landweber算法可转化为约束最优化问题，式（7）的梯度为：

可见，在上述算法中，步长参数γ为定值或取决于ATA和A的范数的实序列{γn}。若‖A‖容易计算，则上述算法是容易执行的，且一般取步长为1/‖A‖2。但是大多数情况下，很难计算‖A‖。依据文献[18]中的方法，下面给出步长参数γ的自适应值，从而避免了计算‖A‖，并给出粘滞迭代格式如下。

自适应粘滞Landweber算法。设x0∈C，n=0,1,2,… ，计算：

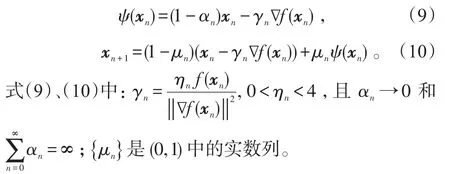
如果对于某一n≥1，xn+1=xn，则xn是一个近似解，迭代停止；否则令n=n+1，继续式（10）计算xn+2。

2.2 问题转化及算法实现

针对式（3）中的反函数求取问题，可以应用上节的显式非线性迭代算法来求解。首先，需要把由S求ρ的非线性问题转化成为第一类算子方程问题；然后，用相关的算法进行迭代运算。

式（3）可表示成：

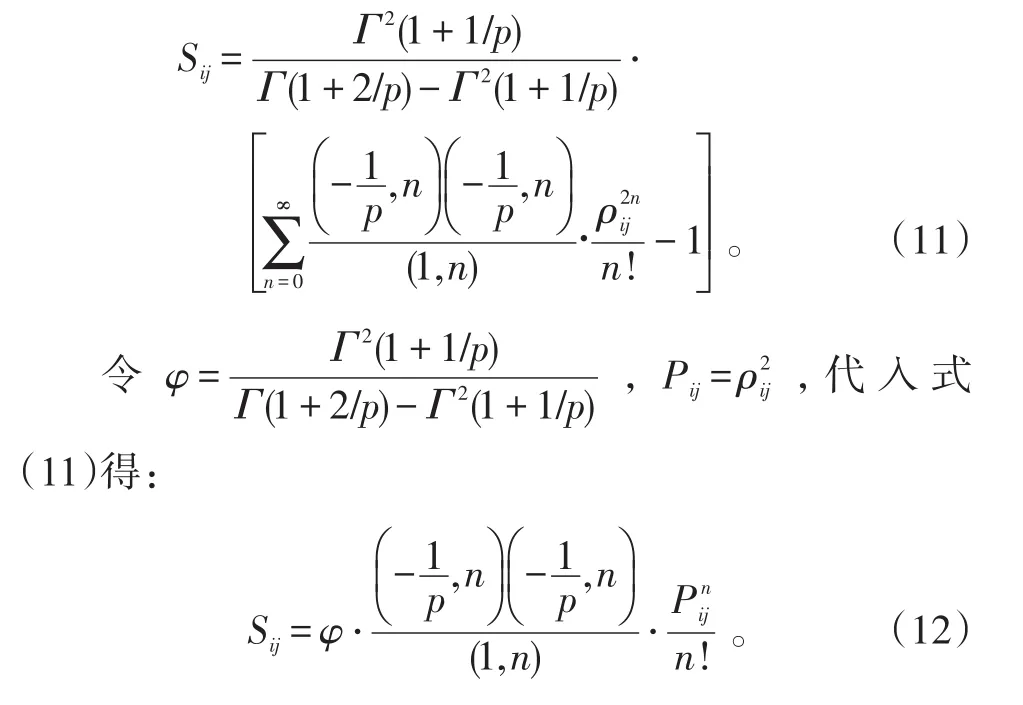
于是可将式（12）的反问题转化成第一类算子方程问题表述如下：

C为高斯分布相关系数空间；定义A=[C⋅Tii]1≤i≤N为N×N阶对角矩阵，其中算子Tii可表示为：

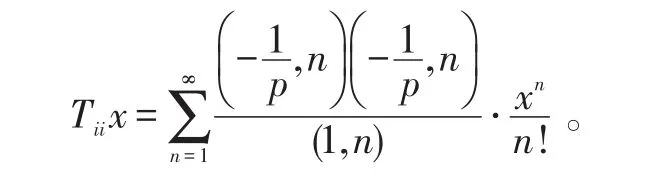
定义Q={S∈RN}，为Weibull分布相关函数空间。其中，N为脉冲数。于是对上述非线性问题可以表述为寻找满足AP=S的向量P，使得P∈C。

利用自适应粘滞Landweber算法实现Weibull随机序列的具体仿真步骤如下：

1）对给定杂波的相关函数序列Sij，利用自适应粘滞Landweber算法求出相关系数序列ρij；

2）产生独立高斯分布的随机序列{vi}，利用步骤1）得到的相关系数序列ρij通过AR模型得到滤波器系数，调制出需要的相关正态序列{ui}；

3）利用式q=(2σ2)1p得到w1,w2～N(0,σ2)中的σ2，产生的w1、w2高斯序列由非线性变换式（2）得到Weibull分布序列{zi}，i=1,2,…,N。

3 仿真结果与分析

为证明利用文中所述非线性迭代算法进行系统辨识，从而模拟相关非高斯雷达波的有效性。本文仿真时假定功率谱为高斯状，其归一化相关函数为[19]：

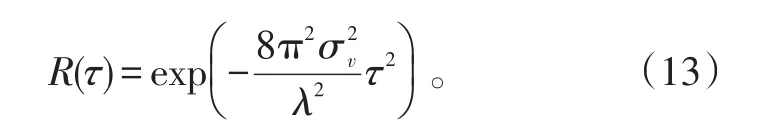
式（13）中：σv为杂波速度的均方根值；λ为工作波长；τ=k⋅PRI，k=0,1,…,N，PRI为脉冲重复间隔，N为脉冲数。

仿真时参数λ=0.03，σv=1 m/s，PRI=0.001 s，N=32。

在仿真过程中，考虑到计算量以及字长等的限制，迭代次数是有限制的。为保证迭代结果是收敛的且达到一定的精度，对式（12）进行计算次数限制，

取K=100以保证计算精度。

在利用Landwever算法和自适应粘滞Landweber算法进行计算时，由于A的定义中含有算子Tii，因此近似的取A=C⋅IN×N，从而令定步长γ=1/‖A‖2。在改进的算法中，取ηn=1/n，αn=1/n。

在雷达杂波模拟过程中，取p=1.5，q=2.2。分别利用2.1节中的显式非线性迭代算法与文献[8]中的隐函数迭代方法进行仿真。对于隐函数迭代、Landwever算法各取迭代次数n=10，对于本文中提出的自适应粘滞Landweber算法仅取n=4。相关函数序列Sij和ρij的关系曲线如图3所示。从图3中可以看出，改进的YLS算法仅用4次迭代就能达到隐函数迭代10次的效果，而Landwever算法的迭代效果最不理想。

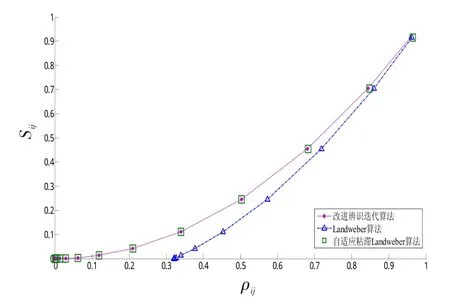
图3 不同迭代算法相关函数序列Sij和ρij的关系曲线Fig.3 Different iterative algorithms of the relation curve of the correlation function sequenceSijandρij

图4为不同算法仿真得到Weibull分布杂波的归一化功率谱密度函数曲线与理论曲线的对比图。从中可以看出，在采用10次迭代的情况下，自适应粘滞Landweber算法的迭代值较好，在仅用4次迭代的情况下，就达到了与理论曲线最好的拟合程度。

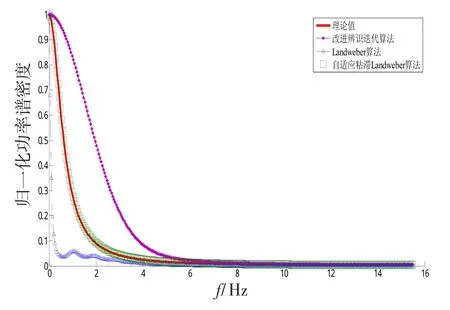
图4 不同迭代算法Weibull杂波功率谱密度函数曲线比较Fig.4 Comparison of power spectral density function of Weibull hybrid power spectrum in different iteration algorithms

通过对上述不同迭代算法的仿真结果进行比较，可以得出自适应粘滞Landweber算法模拟产生相关Weibull分布杂波序列不仅准确有效，而且需要更少的迭代次数。因此，利用该算法产生的Weibull分布序列时域波形如图5所示。

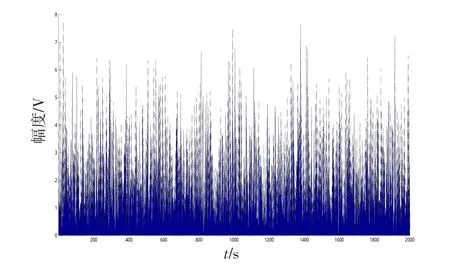
图5 相关Weibull分布杂波时域波形Fig.5 Correlation Weibull distribution cluster time domain waveform

4 结论

本文在基于ZMNL方法模拟Weibull分布雷达杂波的模型中，利用求解正态分布相关系数存在高度非线性的特点，将该非线性问题转化成为第一类算子方程问题。针对Landweber算法的迭代效率低和步长计算的复杂性，提出了一种具备粘滞迭代格式和自适应步长的迭代算法，并用来求解正态分布的相关系数。该方法以显格式的迭代算法代替以往的隐格式的迭代算法，使得问题的求解更加直观、清晰，可以降低杂波数据模拟的运算量。将改进的迭代算法与以往的迭代算相比较，计算机仿真结果表明文中所提出的迭代算法不仅能有效地提高杂波模拟精度，而且能有效地减少迭代次数。这为高效地解决相关Weibull分布雷达杂波模拟问题提供了参考。