浅谈2018年考纲视角下的解析几何复习备考*

福建省龙海第一中学(363100) 曾卫文 柯育仁 苏艺伟

一、2018年考纲对解析几何的要求

2017年12月,教育部考试中心颁布了2018年高考数学考试纲,其对解析几何部分的要求如下:

(1)直线与方程

①在平面直角坐标系中,结合具体图形,确定直线位置的几何要素.

②理解直线的倾斜角和斜率的概念,掌握过两点的直线斜率的计算公式.

③能根据两条直线的斜率判定这两条直线平行或垂直.

④掌握确定直线位置的几何要素,掌握直线方程的几种形式(点斜式、两点式及一般式),了解斜截式与一次函数的关系.

⑤能用解方程组的方法求两条相交直线的交点坐标.

⑥掌握两点间的距离公式、点到直线的距离公式,会求两条平行直线间的距离.

(2)圆与方程

①掌握确定圆的几何要素,掌握圆的标准方程与一般方程.

②能根据给定直线、圆的方程判断直线与圆的位置关系;能根据给定两个圆的方程判断两圆的位置关系.

③能用直线和圆的方程解决一些简单的问题.

④初步了解用代数方法处理几何问题的思想.

(3)圆锥曲线与方程

(1)圆锥曲线

①了解圆锥曲线的实际背景,了解圆锥曲线在刻画现实世界和解决实际问题中的作用.

②掌握椭圆、抛物线的定义、几何图形、标准方程及简单性质.

③了解双曲线的定义、几何图形和标准方程,知道它的简单几何性质.

④了解圆锥曲线的简单应用.

⑤理解数形结合的思想.

(2)曲线与方程

①了解方程的曲线与曲线的方程的对应关系.

上述内容与2017年高考数学考试大纲基本一致.因此2018年的解析几何高考命题应该会继续延续2017年的相关做法,仍然是在考查基础知识的基础上,注重对解析几何所渗透的数学思想方法的考查.重视试题间的层次性,合理调控综合程度,坚持多角度,多层次的考查,努力实现全面考查综合数学素养的要求.

二、全国卷高考对解析几何重点考查的内容

在考纲的指导下,全国卷的试题中解析几何试题一般有3道,圆、椭圆、双曲线、抛物线一般都会涉及.双曲线一般作为客观题进行考查,多为容易题.解答题一般以椭圆与抛物线为载体进行考查,主要考查定点定值问题的证明以及相关的综合性问题,运算量较大,不过近几年高考适当控制了运算量,难度有所降低.

三、2017年全国卷高考试题举例

(1)选择填空

选择填空题主要考查圆,椭圆,双曲线,抛物线的定义,几何性质,基本量的求解.在2017年的三套全国卷中,I卷和II卷都考查了一道选择和一道填空,而III卷则考查了两道选择题,没有填空题.

题型1求离心率

例1 (2017年全国I卷第15题)已知双曲曲线C:的右顶点为A,以A为圆心,b为半径作圆A,圆A与双曲线C的一条渐近线交于M,N两点.若∠MAN=60°,则C的离心率为____.

解析如图1所示,作AP⊥MN,因为圆A与双曲线C的一条渐近线交于M,N两点,则MN为双曲线的渐近线上的点,且A(a,0),|AM|=|AN|=b,而AP⊥MN,所以 ∠PAN=_30°,点A(a,0)到直线的距离在 Rt△PAN中,代入计算得a2=3b2,即由c2=a2+b2得c=2b,所以

图1

例2 (2017年全国卷II第9题)若双曲线C:1(a＞0,b＞0)的一条渐近线被圆(x−2)2+y2=4所截得的弦长为2,则C的离心率为()

解析本题主要考查求双曲线的离心率.双曲线的渐近线方程为bx±ay=0,圆心(2,0)到渐近线距离为则点(2,0)到直线bx+ay=0的距离为即整理可得c2=4a2,双曲线的离心率

例3 (2017年全国III卷第 10题)已知椭圆C:的左、右顶点分别为A1,A2,且以线段A1A2,为直径的圆与直线bx−ay+2ab=0相切,则C的离心率为()

解析本题考查求椭圆的离心率.圆的方程为x2+y2=a2,由于直线与圆相切,所以解得

方法总结离心率是椭圆和双曲线最重要的几何性质.求离心率(或离心率的取值范围),常见有两种方法:①求出a,c代入公式②只需要根据一个条件得到关于a,c的齐次式,然后等式(不等式)两边分别除以a或a2转化为关于e的方程(不等式),解方程(不等式)即可得或取值范围.

题型2求双曲线的标准方程

例4 (2017年全国 III卷第 5题)已知双曲线C:的一条渐近线方程为且与椭圆有公共焦点,则C的方程为()

解析本题主要考查求双曲线的方程.双曲线C:的渐近线方程为椭圆中c=3,即双曲线的焦点为(±3,0).故双曲线的方程为

方法总结求双曲线标准方程的基本方法是待定系数法.具体过程是先定形,再定量.即先确定双曲线标准方程的形式,然后再根据a,b,c,e及渐近线之间的关系,求出a,b的值.如果已知双曲线的渐近线方程,求双曲线的标准方程,可利用有公共渐近线的双曲线方程为再由条件求出λ的值即可.

题型3抛物线的几何性质

例5 (2017年全国II卷第16)已知F是抛物线C:y2=8x的焦点,M是C上一点,FM的延长线交y轴于点N.若M为FN的中点,则|FN|=___.

解析如图2所示,不妨设点M位于第一象限,设抛物线的准线与x轴交于点F′,作MB⊥l与点B,NA⊥l与点A,由抛物线的解析式可得准线方程为x=−2,则AN=2,FF′=4,在直角梯形ANFF′中,中位线由抛物线的定义有MF=MB=3,结合题意有MN=MF=3,故|FN|=|FM|+|NM|=3+3=6.

例6 (2017年全国I卷第10题)已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,则|AB|+|DE|的最小值为___.

图3

解析如图3所示,设直线AB方程为y=k(x−1),由得k2x2−(2k2+4)x+k2=0.设A(x1,y1),B(x2,y2),则由韦达定理得x1x2=1,故由于直线DE⊥AB,所以只需用代替上式中的k,即得|DE|=4+4k2.因此

方法总结抛物线的定义是解决抛物线问题的基础,它能将两种距离(抛物线上的点到焦点的距离,抛物线上的点到准线的距离)进行等量转化.如果问题中涉及抛物线的焦点和准线,又能与距离联系起来,那么用抛物线定义就能解决问题.因此涉及抛物线的焦半径、焦点弦问题,可以优先考虑利用抛物线的定义转化为点到准线的距离,这样就可以使问题简单化.

(2)解答题

题型1求轨迹方程

例1 (2017年全国II卷)设O为坐标原点,动点M在椭圆C:上,过M作x轴的垂线,垂足为N,点P满足

(1)求点P的轨迹方程.(2)略.

解析设P(x,y),N(x,0),M(x,y0).由得故代入椭圆C:得x2+y2=2.

方法总结求动点轨迹方程常常采用以下方法.

1.直译法.直接将动点满足的的几何等量关系翻译成动点x,y,所得方程即为所得动点的轨迹方程.

2.定义法.若动点运动的几何条件恰好与圆锥曲线的定义吻合,可直接根据定义建立动点的轨迹方程.用定义法求解可先确定曲线的类型与方程的具体结构式,然后用待定系数法求解.

3.代入法.动点是直线被圆锥曲线截得的弦中点,只要通过代点作差并以弦的斜率作为过渡,即可获得动点的轨迹方程.事实上这就是中点弦问题的处理方法.

4.参数法.当动点坐标满足的等量关系不容易直接找到时,可以选取与动点坐标有密切关系的量(如角,斜率,比值等)作为参数t,根据已知条件求出动点的参数式方程,然后消去参数即可得动点的轨迹方程.

题型2直线过定点问题

例2 (2017年全国I卷)已知椭圆C:b＞0),四点P1(1,1),P2(0,1),中恰有三点在椭圆C上.

(1)求C的方程

(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为−1,证明:l过定点.

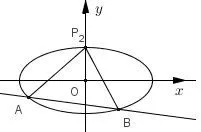
图4

解析如图4所示,当直线l斜率不存在时,设l方程为x=m,A(m,yA),B(m,−yA).由已知有即解得m=2.此时直线l与椭圆只有一个公共点,不符合题意.当直线l斜率存在时,设直线l方程为y=kx+t,1.联立,得(1+4k2)x2+8ktx+4t2−4=0.设A(x1,y1),B(x2,y2),P2(0,1).则由韦达定理得由已知有即此时直线l方程为y=kx−1−2k=k(x−2)−1,故l过定点(2,−1).

例3 (2017年全国II卷)

设O为坐标原点,动点M在椭圆C:上,过M作x轴的垂线,垂足为N,点P满足

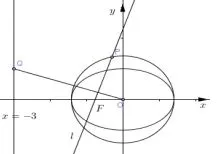
图5

(1)求点P的轨迹方程(略).(2)设点Q在直线x=−3上,且证明:过点P且垂直于OQ的直线l过C的左焦点F.

解法1 由于要证明直线l过左焦点F(−1,0),则可以先求出直线l的方程,再检验F(−1,0)满足该方程.如图5所示,设P(m,n),Q(−3,t),F(−1,0),O(0,0).直线l的斜率为直线l的方程为即3x−ty=3m−tn.由得3m−tn=−3,代入上式得3x−ty=−3.该方程对任意t∈R恒成立,故直线l过左焦点F(−1,0).

解法2 由于直线l过点P且垂直于OQ,故要证直线l过C的左焦点F,等价于证明PF⊥OQ.如图5所示,设P(m,n),Q(−3,t),F(−1,0),O(0,0). 由得3m−tn=−3.又3+3m−tn=0,故PF⊥OQ,因此直线l过C的左焦点F.

方法总结证明动直线过定点的解题步骤可归纳如下.

一选:选择参变量.需要证明过定点的动直线往往随某一个量的变化而变化,可选择这个量作为参变量.当动直线涉及到的量较多时,也可选取多个参变量.

二求:求出动直线的参数方程.求出只含上述参变量的动直线方程,并由其它辅助条件减少参变量的个数.最终使动直线方程的系数中只有一个参变量.

三定点:求出定点的坐标.不妨设动直线中所含参数为λ,把直线方程写成形如f(x,y)+λg(x,y)=0的形式,然后解关于x,y的方程组,得到定点的坐标.

题型3综合性问题

例4 (2017年全国III卷)已知抛物线C:y2=2x过点(2,0)的直线l交C于A,B两点,圆M是以线段AB为直径的圆.

(1)证明:坐标原点O在圆M上;

(2)设圆M过点P(4,−2),求直线l与圆M的方程.

解析(1)设A(x1,y1),B(x2,y2),l:x=my+2.由得y2−2my−4=0,即则x1x2=4.故因此故坐标原点O在圆M上.

(2)由(1)可得y1+y2=2m,x1+x2=m(y1+y2)+4=2m2+4.故圆心M的坐标为(m2+2,m),圆M的半径由于圆M过点P(4,−2),因此故 (x1−4)(x2−4)+(y1+2)(y2+2)=0,即x1x2+4(x1+x2)+y1y2+2(y1+y2)+20=0.由(1)可得y1y2=−4,x1x2=4.所以2m2−m−1=0,解得m=1或当m=1时,直线l方程为x−y−2=0,圆M方程为(x−3)2+(y−1)2=10.当时,直线l方程为2x+y−4=0,圆M方程为

方法总结综合性问题一般融合了直线与圆锥曲线的相关性质,体现在知识的交汇处命题的指导思想,需要综合运用各种知识求解.

四.备考策略

基于上述对2018年考纲对解析几何部分要求的解读,以及2017年全国卷对解析几何部分的考查分析,在复习备考中应该把握以下几点.

1.夯实基础,掌握通性通法

熟练掌握以下知识点:①直线的斜率、方程、位置关系的判定、点到直线的距离公式;②线性规划;③圆的方程、几何性质;④圆锥曲线的定义、标准方程、几何性质、弦长公式. 掌握通性通法:如直线与圆的位置关系问题通常转化为圆心到直线的距离问题;直线与圆锥曲线的位置关系问题,通常采用设而不求法及方程的思想,将问题转化为二次方程的有关问题来求解;求离心率问题转化为a,b,c的关系问题;利用直译法、定义法、转代法、参数法求轨迹方程等.

2.注重知识整合,加强综合训练

综合性强是解析几何试题的重要特点,解析几何试题的综合性可概括为两类:一、纵向联系,特别是直线与二次曲线的位置关系;近几年解几试题基本是纵向联系题.二、横向联系,解析几何可与集合、简易逻辑、函数、方程、数列、三角、平面几何、平面向量、不等式、导数等知识点融合,体现在知识交汇处命题的思想,能极好的考查学生的综合能力.

3.强化运算,力求避繁就简

运算繁杂是解析几何最突出的特点.首先,解题中要指导学生克服只重视思路轻视动手运算的缺点.运算能力差是学生普遍存在的问题,不仅在解析几何问题中要加强训练,而且在其他板块中也要注意加强训练,只有把提高学生的运算能力贯彻于教学的过程之中,才能受到较好的效果.其次,要培养学生运算的求简意识,突出解析几何设而不求的运算本色,充分发挥圆锥曲线的定义和利用平面几何知识化难为易,化繁为简的作用.

总之,在准确理解2018年考纲对解析几何要求的基础上,认真研究2017年全国卷解析几何试题,能够帮助我们深刻认识解析几何的教育价值,从宏观整体上理解和驾驭教材,从微观上把握,调控,设计,实施有效的备考策略,进而内化教学理念与素质的提升,从而实现高效复习.