渗透数学文化的高考题

广东省雷州市第八中学(524232) 魏 欣 邓春梅

数学文化试题近年来在高考中一直有所体现.本文对历年渗透数学文化的高考题进行了统计、归类、分析,并加以解读,最后给出了数学文化在教学中的建议,以期达到开阔眼界、积累经验、提高解答渗透数学文化考题的能力.

一、数学文化的内涵

著名数学教育家、华东师范大学数学系张奠宙教授在《数学教学》2015年第9期发表了文章《多一点数学文化的考题》,该文诠释了数学文化的内涵:数学文化指数学的思想、精神、方法、观点、语言,以及它们的形成和发展.数学作为一种文化现象,早已是人们的常识.狭义的数学文化指数学的思想、精神、方法、观点、语言,以及它们的形成和发展;广义的数学文化除上述内涵以外,还包含数学家、数学史、数学美、数学教育、数学发展中的人文成分、数学与社会的联系、数学与各种文化的关系等等.

近几年高考数学试卷出现以数学文化为背景的新颖命题,将数学知识、方法、文化融为一体,有效考查学生在新情境下对知识的理解及迁移运用能力.2017年考纲作出明确要求后,相信以后的高考关于数学文化的命题会加大,应引起师生们的重点关注.

二、渗透数学文化的高考题的统计与分析

以下是近5年高考全国卷(见下表)、2007-2017年其他省份高考卷也均考查渗透数学文化的高考题,由于篇幅关系,此处不再赘述.

近五年全国卷数学文化试题分布统计表

纵观近几年全国各地的高考试题不难看出,渗透数学文化的高考题主要有以下五个特点:

第一、从文理试卷分配看,数学文化背景试题出现在理科数学卷中较多,文科卷相对较少.

第二、从题型和知识点分布看,基本以选择填空题为主,计算题和证明题相对较少.

另外,涉及到的知识点主要集中在立体几何计算与证明、各种几何形体的体积和面积比例计算、数列、算法程序框图、推理、概率、函数等等.其中几何形体、数列、算法程序框图所占比重明显较大,也出现了有关数学史的几何证明题,并且分值较大.

第三、从素材选取来源来看,出自我国数学名著的数学文化真题几乎均来源于《九章算术》、《数书九章》及《算数书》,其中《九章算术》为主.大多以古代社会人们的生活实际和生产实际为背景,且先用古汉语描述,再以现代汉语予以翻译和解析.另外,外国古代数学文化也有涉及,多以数学名题为主.可见,命题者也注意到了数学的文化多元性思想.

第四、从类别和价值上看,涉及数学史料中的古算题、数学名题、数学家人物及优秀成果、数学与其它学科的文化联系所占比例较少.进一步,突出科学价值、人文价值及应用价值较多,突出美学价值较少.

第五、从呈现的方式来看,仅有显性和隐形两种形式.其中,以隐性形式考查方式较多,以显性形式考查方式较少.显性形式是直接给出数学文化背景作为试题的情景或引子,解答与数学文化背景基本无关.而隐形形式是指不直接给出数学文化背景,隐含考查与数学文化相关的知识和思想方法.

二、渗透数学文化的高考题的归类与总结

1.渗透数学文化的几何题

例1 (2017年浙江理科卷第11题)我国古代数学家刘徽创立的“割圆术”可以估算圆周率π,理论上能把π的值计算到任意精度,祖冲之继承并发展了“割圆术”,将π的值精确到小数点后七位,其结果领先世界一千多年,“割圆术”的第一步是计算单位圆内接正六边形的面积S内,S内=___.

赏析本题以我国古代数学家刘徽创立的“割圆术”估算圆周率为载体,主要考查了圆与三角函数,创设的情景具有浓厚的文化底蕴.答案为

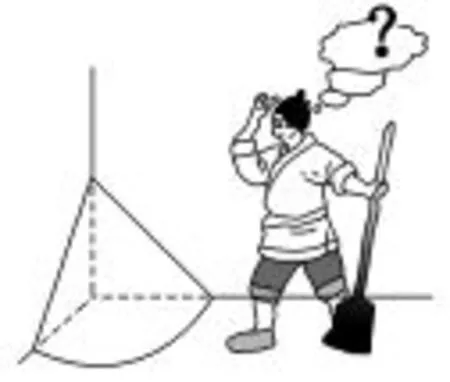
图1

例2 (2015年全国I理科卷第6题)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图1,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有()

A.14斛 B.22斛 C.36斛 D.66斛

赏析本题插图来源于《九章算术》,是本题的一个亮点,其一增强了数学问题的生活化,使数学的应用更贴近学生的生活实际;其二探索了高考数学试题插图的新形式,给出了如何抽象数学问题现象化的范例.本题选B.

例3 (2014年湖北文科卷第10题)《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:置如其周,令相乘也.又以高乘之,三十六成一.该术相当于给出了由圆锥的底面周长L与高h,计算其体积V的近似公式它实际上是将圆锥体积公式中的圆周率π近似取为3.那么,近似公式相当于将圆锥体积公式中的π近似取为( )

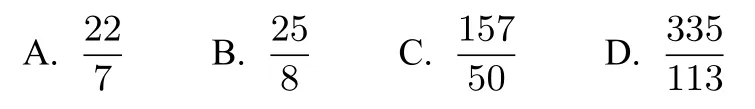
赏析本题源于《算数书》,通过加工改造和加以解析的方式创设了类比推理的情景.试题充分体现了地域特色和数学文化.本题选B.

例4 (2012·湖北理科卷第10题)我国古代数学名著《九章算术》中“开立圆术”曰:置积尺数,以十六乘之,九面一,所得开立方除之,即立圆径.“开立圆术”相当于给出了已知球的体积V,求其直径d的一个近似公式人们还用过一些类似的近似公式,根据判断π=3.14159...,下列近似公式中最精确的一个是()

赏析球是完美的几何体,揭示球的直径与体积之间的关系是中国古代数学的重要研究内容.本题以《九章算术》中“开立圆术”为背景,给出了四个历史上曾经使用过的关于球的直径与体积之间的近似公式.题目没有直接要求考生将四个公式与球的体积公式比较,判断公式的精确性,而是采用了“下列近似公式中最精确的一个是”这种相对隐蔽的独特的设问方式,要求考生自己寻找判别方法,渗透着对考生创新意识的考查.本题选D.

例5 (2013年湖北文科卷第16题)我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水,天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是____寸.(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸)

赏析本题源于《数书九章》,通过加工改造和加注解析的方式降低了理解题意的难度.试题体现了空间想象能力中“无图想图”、“无图作图”的高层次要求,有效地考查了考生提炼图形与应用图形的能力,同时传播了数学文化.著名数学史专家钱宝宗先生对于《数书九章》中提到的“天池盆”作了高度的评价,指出:“天池盆是世界文化史上最早出现的雨量器.”本题答案为3寸.

例6 (2015年湖北理科卷第19题)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图2,在阳马P−ABCD中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE.

图2

(1)证明:PB⊥平面DEF.试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由.

(2)若平面DEF与平面ABCD所成二面角的大小为的值.

赏析本题以课本例题为原型改编而成,主要考查空间直线与平面的垂直以及二面角等基础知识,同时考察空间想象能力和推理论证能力,以及数形结合的思想和转化与化归的思想.此题背景源于《九章算术》卷第五《商功》之[一五].今有阳马,广五尺,袤七尺,高八尺.问积几何;之[一六]今有鳖孺,下广五尺,无袤;上袤四尺,无广,高七尺.问积几何.考题将“阳马”、“鳖孺”相结合,并与课本例题有机整合、巧妙嫁接、精典设问、和谐优美的考题呼之即出.让数学教育者与高考学子为之赞叹.

2.渗透数学文化的数列题

例7 (2017年全国新课标II理3)我国古代数学名著《算法统宗》中有如下问题:远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有().

A.1盏 B.3盏 C.5盏 D.9盏

赏析该题选自明代著名数学家吴敬所著《九章算法类比大全》“塔顶盏灯”问题,后来明朝著名的数学家程大位将这首名题选入《算法统宗》.显然,这是一个等比数例问题,已知塔的层数、灯总和,下层比上一层增加一倍,根据等比数列求和公式可求得塔顶有3盏灯.

例8 (2011年湖北理科卷第13题及文科卷第9题)《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第5节的容积为____升.

赏析本题将数学史与等差数列知识进行融合,注意考查学生的理解问题及知识的迁移应用能力.《九章算术》是中国古代第一部数学专著,是《算经十书》是一部经几代学者整理、删补和修订而成的数学经典著作,系统总结了战国、秦、汉时期的数学成就.全书采用问题集的形式编写,共整理246个问题及解法,分成方田、粟米、衰分、少广、商功、均输、盈不足、方程和勾股共九章.同时,《九章算术》在数学上还有其独到的成就,不仅最早提到分数问题,也首次阐述了负数及其加减法运算法则.它是一本综合性的数学著作,是当时世界上最简练有效的应用数学,它的出现标志着我国古代数学形成了完整的体系.本题答案为

例9 (2012年湖北文科卷第17题)传说古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数.他们研究过如图3所示的三角形数:

图3

将三角形数1,3,6,10,…记为数列{an},将可被5整除的三角形数按从小到大的顺序组成一个新数列{bn}.可以推测:

(1)b2012是数列{an}中的第___项;

(2)b2k−1=____.(用k表示.)

赏析此题是以形为载体,考查数列的通项公式等基础知识,考查特殊与一般的数学思想方法,考查归纳与猜想、推理与计算的能力,试题既合理引用了经典史料,又不刻意增加难度,同时对学生的数感进行了有效地考查,让学生在数学史的背景中,体验数学的理性精神.

3.渗透数学文化的算法题

例10 (2016年全国丙卷理科第8题文科第9题)中国古代有计算多项式值的秦九韶算法,如图4是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=()

A.7 B.12 C.17 D.34

图4

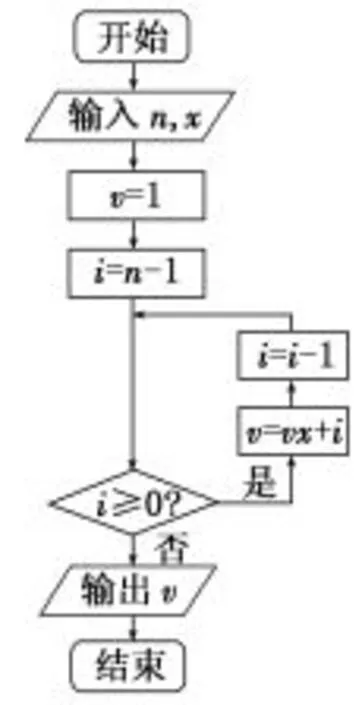
图5

例11 (2016年四川理科卷第6题)秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图5所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例.若输入n,x的值分别为3,2,则输出v的值为()

A.9 B.18 C.20 D.35

例12 (2015年全国卷II文理卷第8题)如图6,程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,18,则输出的a=()

A.0 B.2 C.4 D.14

赏析以上三道题目均来源于我国古代数学名著《九章算术》,主要考查程序框图、“秦九韶算法”和“更相减损术”的知识.

图6

4.渗透数学文化的概率题

例13 (2017年全国I理科卷第2题)如图7,正方形ABCD内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是()

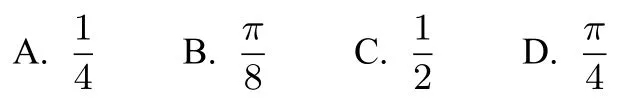
图7

解析本题以我国古代的太极图为背景,考查了几何概型知识,体现数学美学价值.本题答案为B.

例14 (2012年湖北理科卷第2题)《九章算术》是人类科学史上应用数学的最早巅峰,在研究比率方面的应用十分丰富,其中有“米谷粒分”问题:粮仓开仓收粮,粮农送来1534石,验其米内杂谷,随机取米一把,数得254粒内夹谷28粒,则这批米内夹谷约()

A.134石 B.169石 C.268石 D.338石

解析本题以《九章算术》为背景,考查了随机抽样事件的概率知识,体现数学应用价值.本题答案为B.

5.渗透数学文化的逻辑推理题

例15 (2017年全国II理科卷第7题)甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则可推断知道自己成绩的是().

A.乙可以知道四人成绩 B.丁可以知道四人成绩

C.乙、丁以知道对方成绩 D.乙、丁以知道自己成绩

例16 (2016年全国II理科卷第15题)有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是____.

例17 (2014年全国I文理卷第14题)甲、乙、丙三位同学被问到是否去过A,B,C三个城市时,甲说:我去过的城市比乙多,但没去过B城市;乙说:我没去过C城市;丙说:我们三人去过同一城市.由此可判断乙去过的城市为____.

例18 (2014年北京理科卷第8题)学生的语文、数学成绩均被评定为三个等级,依次为“优秀”“合格”“不合格”.若学生甲的语文、数学成绩都不低于学生乙,且其中至少有一门成绩高于乙,则称”学生甲比学生乙成绩好”.如果一组学生中没有哪位学生比另一位学生成绩好,并且不存在语文成绩相同、数学成绩也相同的两位学生,那么这组学生最多有()

A.2人 B.3人 C.4人 D.5人

赏析以上四道题目主要考查逻辑推理能力及分析问题、解决问题的能力.试题要求考生从文字语言中精确抽取有用的信息,加工信息,并利用各信息中的逻辑关系,通过逻辑推理,最终做出正确的判断.

三、数学文化在教学中的建议

1.在知识引入部分注重体现数学文化.

知识的引入部分是体现数学文化的一个重要途径,我们可以从多方面来体现数学文化,如:数学知识的发生、发展的背景,数学知识的应用、数学知识与社会发展的关系,与此知识相关的趣闻轶事,数学家的故事、精神,以及含有此知识的自然资源、人文遗产等.

2.借助数学文化突破教学难点.

如对高中函数的概念的教学,如果采取传统的先给出定义,再举例、练习强化的方式进行教学,往往效果不佳.教学中可以利用函数概念的发展史,从变量说引入,到对应说,到关系说,再合理应用一些特殊函数如符号函数和高斯函数等,可以帮助学生理解函数概念和本质,从而提升学生对学科本质的认识.

3.在解题的过程中渗透数学文化,尤其是历史上的数学名题.

数学名题和数学猜想是无数先贤细致思考和用心钻研的结晶,它们无不很好的促进了数学的不断前进.历史上许多数学名题不仅能展现出其所在的历史背景,且都展现着某些重要的思想方法和独特的数学魅力.例如古希腊三大几何问题、哥尼斯堡七桥问题、哥德巴赫猜想等.

4.善用教材中隐形数学文化知识进行拓展训练.

当前教材中出现了许多高考数学文化命题素材来源题.如“阿波罗尼圆”、“回文数”、“三角形数”分别出现在人教版高中数学必修2第131页习题4及必修3第51页第3题和必修5第28页的正文部分.因此,教师上课时要有意识地对这些数学文化素材或历史名题进行拓展改编.比如根据布洛卡点的基本性质,就可以结合余弦定理、外森比克不等式和等比数列等知识拓展许多变式问题.

5.在课堂小结中注重体现数学文化.

课堂小结不仅仅是对知识点的总结,更重要的是对数学思想方法的总结,对数学应用价值的总结.在课外阅读中注重体现数学文化.教材的拓展性栏目提供了丰富的数学文化素材,教师应该引导学生阅读、思考、操作,并注意从中引导、总结数学家的探索精神、理性精神、求实精神等数学精神,以及数学与社会发展、生活实际的联系等.

数学作为一种文化,体现在数学的方方面面.教材相当重视数学文化,几乎教材的每一部分都含有数学文化的内容,我们教师应该主动去发掘开发这些内容,并将数学文化与教学实践有机地结合起来,使数学文化贯穿到教学实践的全过程.这样做,使数学史的应用深入到学生的认知层面,有利于培养学生的数学思维能力和数学问题意识.张奠宙教授指出:“数学史必须走进课堂,在实际教学中使得学生在学习数学的过程中真正感受到文化感染,产生文化共鸣,体会数学的文化品味和人情味.”