利用三角函数f(x)=sin(ωx+φ)的性质求参数ω的最值问题

广东省中山市实验中学(528400) 王明义

三角函数的图像是三角函数的重要表示方法之一,它完美地体现了数形结合的思想,具有直观形象、规律明显的特点.在高考中,这部分内容主要以客观题的形式出现,分值在5分左右,偶尔以解答题的形式出现加以考察,多数题目试题难度中等.在2016年的理科全国I卷高考试题中,与三角函数的图像有关的试题共15道,其中8道题考查了三角函数的图像的变换.认真研究高考题是复习备考的捷径,因为高考题有考点准确、信度好、方向明、内容精、成本低、效益高的特点,因此,高考题有着极高的训练和研究价值.

本文作者以2016全国理科数学I卷的第12道选择题为出发点,对这类问题做一个深入的探究,得到三角函数中一些常用的结论,并利用这些结论方便地解决了一些类似的数学问题.

一.问题提出

题目(2016年全国卷I第12题)已知函数f(x)=sin(ωx+φ),为函数的零点,为对称轴,且函数在区间上单调,则ω最大值()

A.11 B.9 C.7 D.5

解法一(解析法)依题意有

解方程得

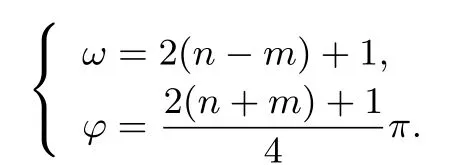
(1) 当m+n=0时,ω=4n+1,又因为得到ω≤12.依题意取n=2得到ω=9,经验证符合单调性要求.

(2)当m+n=−1时,ω=4n+3,取n=2得经验证函数不满足单调性要求故舍去.

综上所述,答案B满足要求.

解法小结这种解法我们称为解析法,它是利用已知条件采用列方程的方式,来计算出参数的值,这个解法思路比较简单,但是实际操作起来计算量偏大,而且不够直观.下面我们利用三角函数的图像推导出4个性质,然后利用这些性质解决这个问题.

二.与函数f(x)=sin(ωx+φ)有关的四个性质

性质1 函数f(x)=sin(ωx+φ)的某一个零点与某一条对称轴的距离d和周期T的关系:

证明不妨设函数的零点为x1,对称轴为x=x2,则由零点和对称轴的性质可以得到:

证毕.

性质2 若函数f(x)=sin(ωx+φ)在某区间上单调,则此区间的长度d与最小正周期T的关系为:

此结论由三角函数的图像易得,证明从略.

性质3 对于函数f(x)= sin(ωx+φ),若满足f(x1)=f(x2),则为函数的一条对称轴或者|x1−x2|=kT,k∈N.

证明因为f(x1)=f(x2)所以

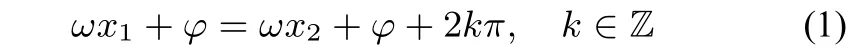
或者

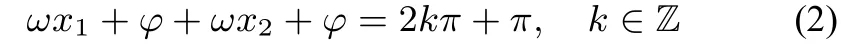
性质4 对于函数f(x)=sin(ωx+φ),若f(x1)=−f(x2),则为函数的一个零点或者

证明若f(x1)=−f(x2)我们得到:

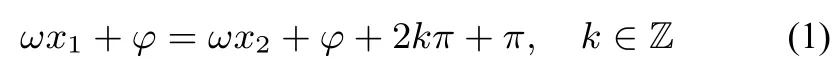
或者

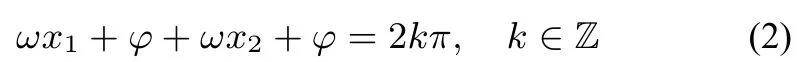
由(1)得

由(2)得

三.应用举例

例1 首先我们利用上述性质来解决文章开头的高考题.

解答由性质1和性质2我们可以得到:

从而得到ω=2n+1且ω≤12.根据题意和四个选项中的答案,我们先令ω=11进行排除,得到此时n=5.由(1)得对称轴和零点的距离为下面我们就在零点和对称轴之间作出个周期的图像,如图一.其中黑色加粗部分为给定区间上的图像.由于不符合在单调性的要求故排除.

然后我们再令ω=9,此时n=4.同理可得到对称轴和零点的距离此时为同理,在零点和对称轴之间作出个周期的图像,如图二.易知此时满足单调性的要求,答案选B.

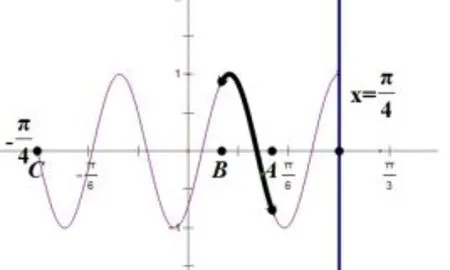
图1

图2

例2 (2014年北京理科第14题)设函数若f(x)在区间具有单调性,且试问f(x)的最小正周期是多少?

解答由性质2我们可以得到所以所以再有性质3和可知为对称轴.再由性质4和可知为函数的一个零点.再利用性质1得即所以T=π.

此题的解答过程完美的体现了上述4个性质的应用,简单明了,赏心悦目.

例3 已知函数且在有最小值无最大值,则ω为多少?

解答因为函数在内有最小值无最大值,所以在区间内的图像大致为图3所示.则由性质2可知对称轴为且所以即ω=且ω＞0,故

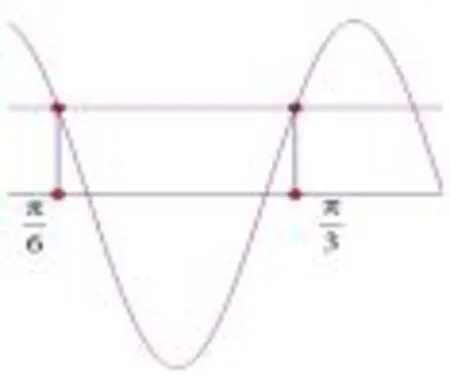
图3

四.备考复习建议

(一)夯实基础,重点突破

三角函数图像问题的核心在于如何作图和识图,所以我们要打好利用“五点法”作图和利用“图形变换法”作图这两个基础,方能在解题的时候以不变应万变,用最快捷和高效的方法解决问题.

(二)一题多解,变式训练

现在的高考题灵活多变,我们不能够一味的机械模仿,重复做一些“经典好题”.否则,一是忽略了数学的本质,二是导致学生慢慢失去学习数学的乐趣.所以我们要进行适当的变式训练,从而克服如上弊端.当然,变式训练要围绕学生的易错点展开,训练学生解决灵活性问题的能力,让学生不断积累,做到举一反三.

(三)数形结合,锻炼思维

上面的例题中,我们主要是利用三角函数的图像观察出四个性质,这就是数形结合的思想的应用.数形结合的思想是数学知识在更高层次上的抽象和概括,高考中会面临对这方面的重点考查.因此,通过复习提升学生高阶思维能力,也是我们今后学习过程中的重中之重.