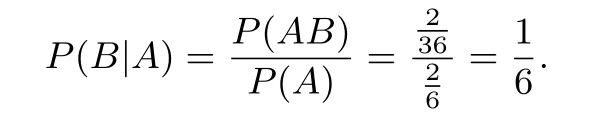一个条件概率问题的辨析

广东省广州市第七中学(510080) 陈武生

一、问题的提出

文［1］指出了教学中容易被师生疏忽的有关条件概率的问题,读后很受启发.最近,笔者所在学校使用了如下的一道题目进行高三测试,结果再次引起了大家的争论与反思.

原题(广州某地高中毕业综合测试题)抛一枚均匀的骰子(骰子的六面分别有数字1,2,3,4,5,6)来构造数列{an},使

原标准答案(1)从略.(2)若或即前2次抛骰子中都是奇数或都是偶数.若前2次都是奇数,则必须在后5次中抛出3次奇数2次偶数,其概率:若前2次都是偶数,则必须在后5次中抛出5次奇数,其概率:所以所求事件的概率

可以看出,原标准答案中把第二问看成是积事件.

二、问题的讨论

两种与原标准答案不同解答测试后发现,相当多的学生把第2问看成是条件概率来解.学生解法中,除标准答案的方法之外,还有以下两种:

解法一(缩小样本空间法)所求概率为

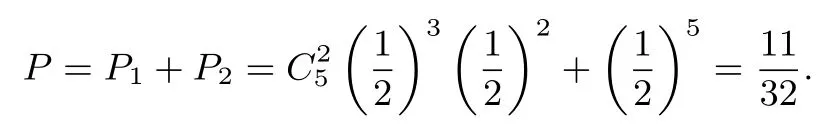
解法二(据条件概率公式计算)设

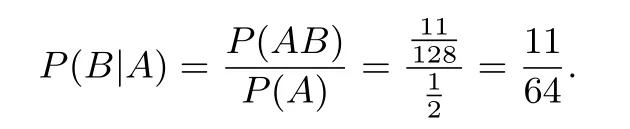
按文［1］说法,本题第2问应使用条件概率.本文不想在是否用条件概率的问题上做太多的文章,相信在以后的各类考试中,命题者会在措词上给出明确的表述.笔者认为,本题第二问是条件概率问题,所以原标准答案是错误的.现在的问题是,以上解法一、解法二为何结果不同?

三、原因分析

(i)对于解法一,可从独立性方面分析如下:由题目知,前两次的结果与后面几次的结果之间没有关系,即所求为:P(B|A)=P(B′),其中B′为换句话说,A与B′相互独立,所以解法一正确.

(ii)对于解法二,初看难于发现结果与解法一相异的原因.从解题过程,我们可作以下的分析:

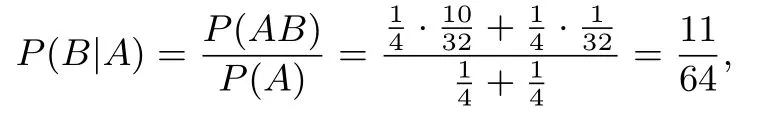
解法三

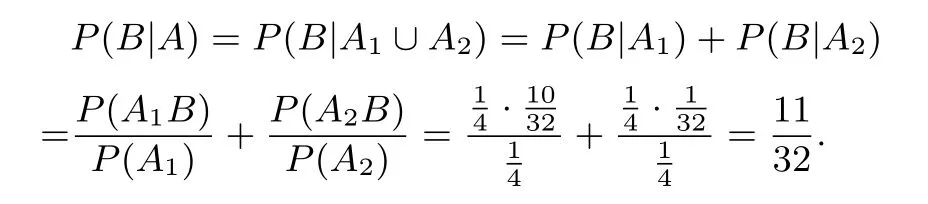
归纳总结事实上,解法三就是全概率公式,高中的教材并没有涉及;根据文[2],为了求得较复杂事件R的概率,可以先把它分成两个(或若干个)互不相容的较简单事件之并,利用加法公式求得.全概率公式如下:设B1,B2,···是一列互不相容的事件,且有则对于任一事件A,有

下面再举一例子来说明问题.

例1 有两个箱子,1号箱中有2个白球和4个红球,2号箱中有5个白球和3个红球,现随机从1号箱中选出1个放入2号箱,然后从2号箱中随机选出一个球,试给出从2号箱中取出红球的概率?

分析这里用全概率公式求解.

解因为从1号箱中选出白球的概率记为B1;从1号箱中选出红球的概率记为B2;1号箱中选出的为白球时,从2号箱中取出红球的概率为1号箱中选出的为红球时,从2号箱中取出红球的概率设所求的事件为R,则

四、一些建议

1.命题应严把文字关,对于易引起混淆的语义,应进行修改;历年高考命题都遵守这个原则.

2.条件概率的教学应把握难度,不应出太难的题,但对这个概念本身,力求在教学中讲透.对于本题的解法二为何出错,学生也许不能真正理解,还可以用以下题来说明:

变式投掷骰子两次,求在第一次掷得的点数为1或2的条件(设为A)下,两次掷得的点数之和为5(设为B)的概率.

由于可以列举法证得,学生更容易理解.

解法一(正确解法)容易求得所求概率为

解法二(错误解法)所求为