椭圆的第三定义

广东省佛山市罗定邦中学(528300) 龙 宇

广东省佛山市李伟强职业技术中学(528300) 何 珊

1.第三定义的由来

在人教A版教材–选修2-1的第80页有如下一道习题:

10. 已知△ABC的两个顶点A,B的坐标分别为(−5,0),(5,0),且AC,BC所在直线的斜率之积等于m(m̸=0),试探求顶点C的轨迹.

此题的目的是为了介绍圆锥曲线的第三定义,但介绍的过于浅显.根据高考的考纲,教材中出现的任何内容都可能作为高考的出题点.所以本文以椭圆为例,介绍一下椭圆的第三定义,再给出几个例题供大家参考.

定义平面内的动点到两定点A1(−a,0),A2(a,0)的斜率乘积等于常数e2−1的点轨迹及点A1,A2叫做椭圆,其中的常数e2−1∈(−1,0).

说明因为当椭圆上的点与端点重合时,斜率不存在,所以该定义要特别注意两个端点.

2.第三定义的运用

例1 已知椭圆E:的离心率其左、右顶点分别为点A,B,且点A关于直线y=x对称的点在直线y=3x−2上,点M在椭圆E上,且不与A,B点重合.(1)求椭圆E的标准方程;(2)已知点N在圆O:x2+y2=b2上,MN⊥y轴,若直线MA,MB与y轴的交点分别为C,D.求证:sin∠CND为定值.

分析第(1)问较简单,E的标准方程为过程从略.第(2)问中求证∠CND的正弦为定值,而与正弦相关的结论较少,转求该角的余弦值,若该角的余弦为定值,正弦必为定值.

因为点M在椭圆E上,设点M为又因为点N在圆O:x2+y2=b2上,且MN⊥y轴,所以点N为设直线MA的斜率为m,直线MA为:得到点C的坐标为同理,设直线MB的斜率为n,得到点D的坐标为通过向量的方法来计算∠CND的余弦,

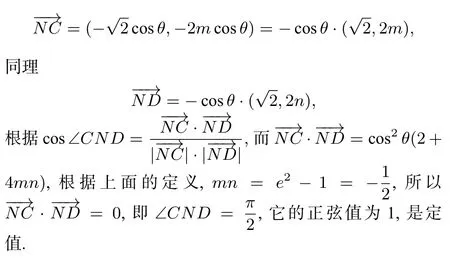
该类问题的传统解法,是用尽量少的未知数(即“消元”思想)表达出所求式,再计算出最终的定值.而该解法以直线斜率做为参数,增加了较多的未知量,与学生们“固有的”消元思想相违背,虽然能更好表达题目的意图,但解答的过程会越来越复杂,以最后的向量为例,我们一共有三个未知量,对于解答者而言,需要较强的心理承受能力,才能继续化简.但是该解法通过第三定义,在最后一步消掉所有的未知量,能给人一种豁然开朗的感觉,很有一种数学的奇异之美.

例2 (2016年广州一模第20题)已知椭圆C的中心在坐标原点,焦点在x轴上,左顶点为A,左焦点为F1(−2,0),点在椭圆C上,直线y=kx(k̸=0)与椭圆C交于E,F两点,直线AE,AF分别与y轴交于点M,N.

(1)求椭圆C的方程;

(2)以MN为直径的圆是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.

分析第(1)问中椭圆方程为:过程从略.对于第(2)问,主体思路都是联立直线与椭圆,求解得到点E,F,进而得到点M,N,然后以点M,N为直径做圆,再观察表达式,判断该圆是否过定点.思路虽清晰,但运算太过复杂.根据题干信息,点E,F关于原点对称,可直接设点E(x1,y1),点F(−x1,−y1),虽可以简化部分运算,但仍很复杂.

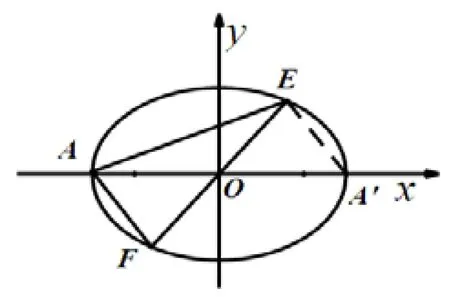
图1

在证明该问之前,我们先利用椭圆的第三定义得到如下的

断言设直线AE,AF的斜率分别为m,n,则有

事实上,设椭圆的右顶点为A′,则有点A与点A′关于原点对称,点E,F也关于原点对称,则有直线EA′的斜率等于AF的斜率n,利用椭圆的第三定义,

解直线AE,AF的直线方程分别为它们与y轴的交点分别为以MN为直径的圆的方程为:

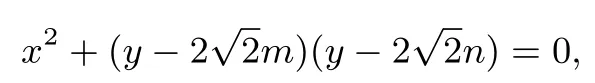
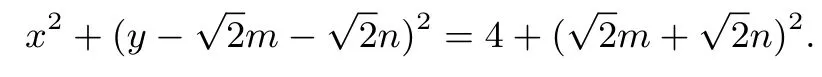
根据方程可知,该圆过定点为(±2,0).

总结两道例题的本质是一样的.根据例1,点P落在圆x2+y2=4上.如果把两题结合起来,我们可以编出下面的练习供读者思考

练习已知椭圆C:直线y=kx与椭圆C交于点E,F,设椭圆上的任意一点P,直线PE,PF与y轴交于点C,D,设点N在圆O:x2+y2=b2上,且PN⊥y轴,求证:CN⊥DN.

证明过程如上例,从略.

例3 设P为椭圆C:上的动点,F1,F2为椭圆的两个焦点,I为△PF1F2的内心,求点I的轨迹方程.

解在求轨迹方程之前,我们先证明如下的

断言设焦点三角形的底角为α,β,则有

事实上,设焦点三角形的顶角为γ,注意到由正弦定理可得

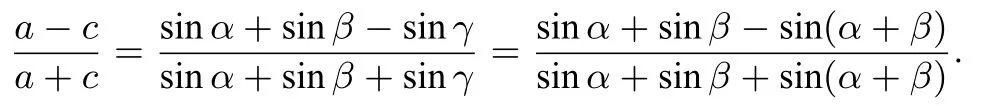
仿照上面的解法二,利用和差化积及二倍角公式可得:

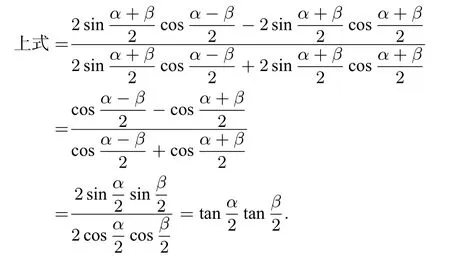
回归到焦点△PF1F2即有为定值,且该定值位于(−1,0).根据椭圆的第三定义,点I的轨迹为椭圆,其方程为: