试析中考数学综合题常见类型
2018-08-08翁为科
翁为科
(深圳市罗湖高级中学初中部,广东 深圳)
中考数学中习题开放性主要是指,条件不完善,结论没有明确同时也不唯一,解法没有严格限制,这样在解题中学生便留有充分的认知空间。题目在解题中充分体现了创新精神,因此在中考中比例持续加大,现在要求教师对这些开放性习题的类型以及解题策略进行分析研究,引导学生通过分析、比较、猜想等多种思维方式进行探究。
一、中考中的常见数、式题型
为了使学生对中考题目有系统认识,一定要针对性地对常见题型剖析,不断深化感性认识。
计算类习题,数和式综合使用。
在此种题目中要先进行简化,之后求值。
此类计算题,主要是为了考查学生数字和式子之间综合运算能力,在很多地方中考中都有出现。此类习题为基础性题目,在计算中重视不够,便经常会出现各种错误;同时涵盖知识点较多,学生学到的各种数字和式子都有涉及,有任何问题没有考虑到便会失分。做此种类型题目一定要保证:第一,记熟特殊角三角函数值,同时要掌握好负指数幂以及整数指数幂、二次根式、平方根、绝对值、实数在运算中的顺序以及运算法则;第二,掌握好整式加减、乘除、因式分解和通分、约分以及分式之间的乘除运算。在分式化简中一定要重视x值是否能够确保分式有意义。
二、中考中的方程以及不等式组、函数综合问题
例题:为了在长假高峰购物做好准备,运动服装品牌店主要采购两类服装,分别为甲类、乙类。两种货物的购买价格和出售价格如下。

运动服装价格 甲 乙类进价(元/件) m m-20售价(元/件) 240 160
购货时,货款中3000元购买甲类服装的件数和2400元购买乙类服装数量一样。
(1)得到m值。
(2)购买甲类和乙类服装中,200件总利润一定在21700元之上,同时低于22300元,现在分析在专卖店内一共有哪几种进货方式?
(3)在第二条条件中,专卖店要对甲种服装进行优惠促销,同时决定对甲类服装进行优惠a(50<a<70)元,乙类服装售价不变。现在分析专卖店中要想得到最大利润要使用哪种进货方式?
解:(1)根据题意可以看出3000/m=2400/m-20,可以得到m=100,在验证之后可以得到m=100为方程解,因此可以得到m=100。
(2)进购甲类服装x件,乙类服装一共(200-x)件,从题意可以看出。
(240-100)x+(160-80)(200-x)≥21700,①
(240-100)x+(160-80)(200-x)≤22300,②
可以得到95≤x≤105。∵x为整数,105-95+1=11,∴会有11种方案。
(3)设总利润为 w,w=(140-a)x+80(200-x)=(60-a)x+16000(95≤x≤105)。
①中 50<a<60 时,60-a>0,其中 w 随着 x变大同时变大。专卖店在x=105时可以发现,w中有最大值。因此可以得知,购买甲种服装105件时,购买乙种衣服为95件。
②在a=60时可以看出,60-a=0,w=16000,可以看出两种方案获利都相同。
③在60<a<70中,60-a<0,同时w会随着x的变大不断减小,在x=95时w一定有最大值。因此可以购买甲种服装95件,乙种服装105件。
这种类型的题为分式方程、一元一次不等式组、一次函数。处理这些问题的关键点在于读懂题意,同时找出描述性词语,列出所求的不等关系以及等量关系。处理第三问时不仅要将其中的实际问题“利润”转变为一次函数,同时也要充分结合一次函数性质,依据一次函数状况进行分类研究。方程和函数之间相互结合的综合题,也是考试重点[1]。函数和方程虽然为不同的数学概念,但是相互关联和渗透,很多方程问题都可以使用函数进行处理,同时也可以使用方程处理函数问题。这些问题关键要重视变化和联系,可以分析抽象的数量特征,实现函数和方程之间的相互装换,从而起到解决问题的作用。
三、统计和概率综合
在统计类题中考点主要有抽查、全面调查,平均数、中位数和众数,这些主要是反映了数据集中性,考试中要考查学生在各种背景中使用各种数代表每种数据,或者统计图找出数中特征、极差以及方差,两者主要是反映数据之间的波动,描述稳定性,在对两组数据进行比较时一般会先观察平均数,之后才会使用方差。
例题:在方格中,A、B、C、D、E、F都处在正方形顶点。(1)A、D、E、F四点中任意选择一点,选择的点主要以B、C作为顶点画出三角形,求得到等腰三角形的概率。
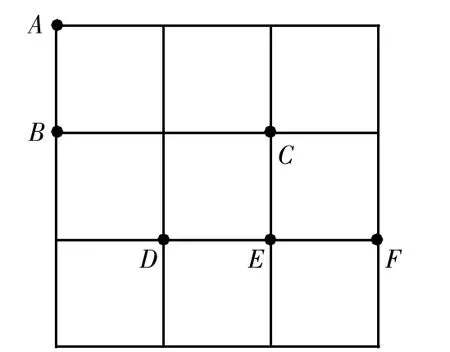
(2)从 A、D、E、F这四点中任意取两个点,取得点和 B、C 作为顶点画出四边形,计算出可以得到平行四边形的概率(树状图、列表求解)。
在题中不仅要考查学生使用树状图、列表计算出所有可以得到平行四边形的概率,同时也要使用概率对等腰三角形进行评判,所考核的知识点综合性强。在解决这些问题时,不仅自己要学会画树状图列表得到各种结果和概率,同时也要掌握图形性质判定知识。
四、二次函数中的综合问题
二次函数主要是探讨具体问题中的数量变化以及在此规律上的抽象数学概念,同时也是研究现实世界规律的模型。二次函数中的重要思想便是用运动观点分析和解决问题[2]。在命题上主要围绕新课标,为了考查学生分析和处理实际问题的能力,确定好二次函数中的表达方法,充分理解函数特征。使用好描点画法做出二次函数图象,在图象中看到函数性质,使用配方、公式等各种方式确定函数图象开口方向以及顶点,使用这种方式得到一元二次方程近似解。
已知二次函数y=ax2+bx+c(a≠0)的图象如下图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③m>2。其中,正确结论的个数是 ( )
A.0 B.1 悦.2 D.3
①二次函数y=ax2+bx+c与x轴有两个交点,
∴b2-4ac>0,故①正确;
②∵抛物线的开口向下,
∴a<0,

∵抛物线与y轴交于正半轴,
∴c>0,
∵ 对称轴 x=b/2a>0,
∴ab<0,
∵a<0,
∴b>0,
∴abc<0,故②正确;
②一元二次方程ax2+bx+c-m=0没有实数根,
∴y=ax2+bx+c和y=m没有交点,
由图可得,m>2,故③正确。
故选:D。
五、阅读以及新定义有关的综合型题目
这些题在以后的数学考试中会逐渐增加,同时考试的很多知识并不属初中数学,更多的是重视初中和高中知识之间的衔接。很多题目都是高中数学知识,或者有一些跨学科的知识。这些主要是考查学生理解能力、阅读能力、使用新知识能力。处理这些问题关键在于认真阅读,同时要理解题目,认识到题目中的新公式、新定义,同时使用这种方式解决和处理相关问题。
例题:在实数中,规定[x]为不大于 x的整数,有[1.2]=1,[4]=4,[-2.6]=-3,假如现在分析x可以为多少 ( )
A.41 B.43 悦.51 D.57
解析:从定义中我们可以看出,[x]主要为小于等于x的最大整数。同时结合例题可以看出要想满足可以得到46≤x<56,因此可以选择第三项。
数学综合题中不仅有这些题,也会有各种变换类型的[3]。但是不论是何种综合题,不仅要对方法进行考查同时也重视综合能力。在学习中一定要抓住知识的关联,掌握好数学思想和方式。只有通过这种方式才可以灵活使用、分析问题、观察问题,解好综合问题。
