日本2017年全国小学数学学力测试试卷

◇编译/陈肖颖 章勤琼

2007年，日本恢复了停止43年之久的全国学力调查，并将其制度化，每年都举行。测试对象为小学和初中毕业年级的学生，内容包括学力测试部分和学习状况调查，前者主要考查学生对日本国语和数学两门基础学科的掌握情况，后者则是为了了解学生的生活习惯及学校环境而进行的问卷调查。去年介绍了2016年日本小学数学学力测试试卷，现介绍2017年的测试试卷。

A卷

1.1m丝带的价格为60日元，请思考如何求下面所需的花费。

（1）买2m丝带需要花多少钱？买3m丝带需要花多少钱？请将答案分别写出来。

（2）买0.4m丝带，此时应花费（ ）日元。丝带的长度和费用的关系如图1所示。“买1m的费用是60日元”“买的长度是0.4m”“买0.4m的费用是（ ）日元”，这些在图1中应该怎么表示呢？在A～E中选择合适的位置，并将上述答案一一标记。

图1

（3）求买 0.4m 的费用的式子是：60×0.4。

为了求出60×0.4的答案，我们像下面这样使用60×4的求法来解答：

图2

方框中F的答案是哪一个呢？请从下面的①～③中选择一个正确答案。

①乘10 ②除以10 ③变化

2.计算下列各题。

（1）123×52；

（2）10.3+4；

（3）6+0.5×2；

（4）5÷9（商用分数形式表示）。

3.写出8和12的最小公倍数。

4.比较装满水的两个瓶子的容量，可以将两个瓶子中的水分别倒入大小相同的杯子中，（图略）并通过倒满水的杯子的数量进行比较。

与这种方法类似，下列物体的质量或长度也分成同样大小的几份来进行比较的是①～④（如图3～6）中的哪几个？选择2个答案，将号码写下来。

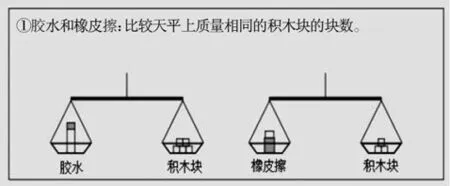
图3

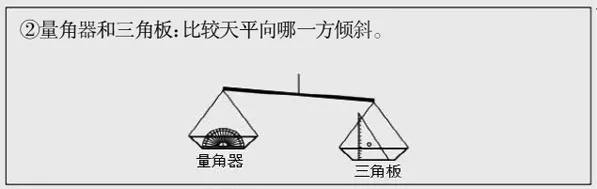
图4

图5

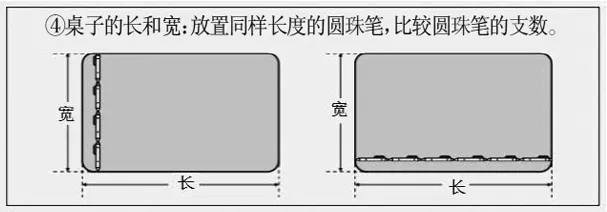
图6

5.利用两条直线，作出平行四边形和三角形。

如图7，①～④中三角形的面积是平行四边形F面积的一半的有哪些？请写出其编号。

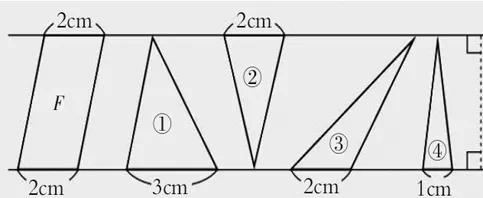
图7

6.如图8，在以点O为圆心的圆内作出正五边形。

首先，作一条半径，与圆相交于点A。

其次，根据点B的位置作一条半径，此时，∠AOB的大小是多少？请写出答案。

图8

7.图9是一个立方体的展开图。

图9

用这个展开图折成立方体后，与着色面平行的面是A～E中的哪一个？从下面①～⑤中选择：

①A ②B ③C和 D ④A、B和 E ⑤A、C、D和E

8.你有一些贴纸，如果平均分给5人，则每人有10张。用式子表示原有贴纸的数量是多少。在下面①～④中，选出合适的答案：

①□×5=10

②10×□=5

③□÷5=10

④10÷□=5

9.就问题“家里是否喂养狗或猫”，我们采访了13个人，情况记录如表1：

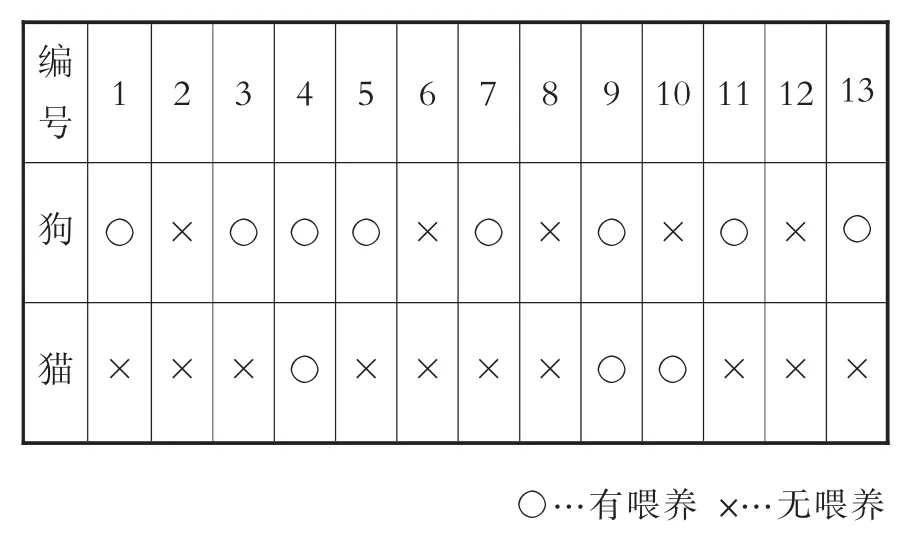
表1 喂养狗或猫的情况记录

整理如下：

表2 喂养狗或猫的情况调查表

（1）表1中编号为1的人应填在表2中A～E的哪个位置？

（2）写出表2中E代表的数。

B卷

1.有编号为1～9的卡片各1张（图略）。从中选取2张并进行排列，交换两位数的2个数字，用较大的数减去较小的数。例：选取和，排成19和91。计算两位数增量：91-19=72。

选取的2张卡片上的数字不同时，我们把它们的差称为“卡片之差”。例如，和这2张卡片的“卡片之差”为8。

绫香将“卡片之差”为1、2、3时选取的2张卡片都做了两位数增量计算（如图10）：

图10

绫香：“卡片之差”为 1、2、3 时，通过计算可知两位数增量分别为9、18、27。

（1）“卡片之差”为4时，写出一个计算两位数增量的式子，并求出答案。

绫香得出“卡片之差”为2、3时两位数增量分别为18、27。下面是她思考的过程：

5 3是 5个 10和 3个 1，35是 3个 10和 5个1。

如图11，图中的⑩代表10，①代表1。

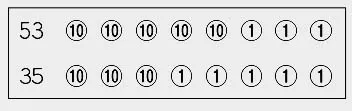
图11

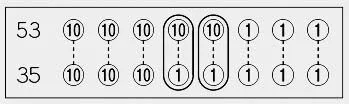
图12

（2）“卡片之差”为1时，用同样的方法（绫香的思考过程）得出两位数增量是9。

图13

（3）这样下来，“卡片之差”为 1、2、3 时两位数增量计算的答案可以总结如下：

“卡片之差”为1时，两位数增量是9。

“卡片之差”为2时，两位数增量是18。

“卡片之差”为3时，两位数增量是27。

如果已知“卡片之差”，就可以很容易得到两位数增量。

如上所述，利用“卡片之差”可以很容易解决两位数增量计算的问题。请用文字和数字写出这个规律。

2.尤里想要给交流会上来自不同地方的20人赠送感谢信和纪念品。

根据信件的大小和质量，单次邮寄的费用如表3：

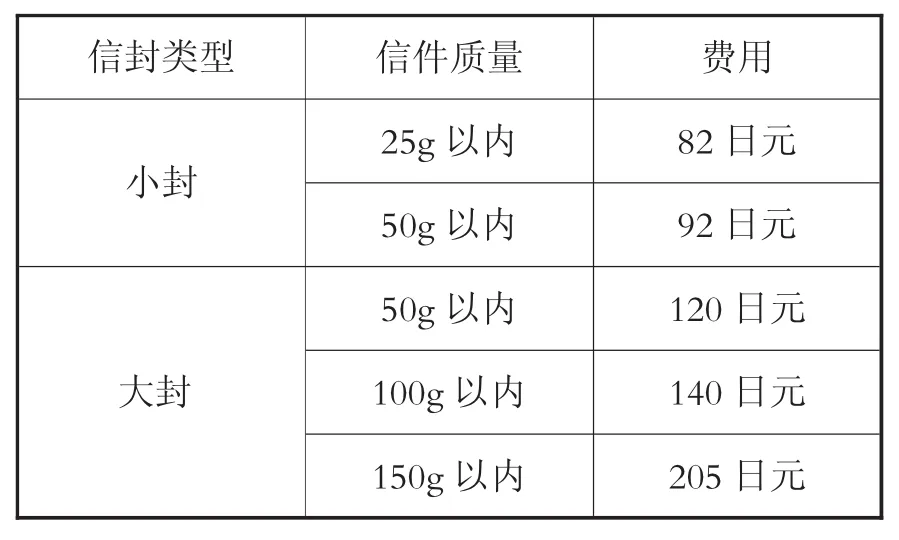
表3 单次邮寄的费用

把感谢信和纪念品放入小封中，1件的质量是27g；放入大封中，1件的质量是36g。尤里为了使费用更便宜，决定使用小封邮寄。

（1）感谢信和纪念品都要装入信封中，思考：邮寄20个信件的费用，装入小封比装入大封便宜多少钱？要求写出表达式，再写出答案。

为了放入小封中，需要把长方形的信折成长条形（如图 14）。

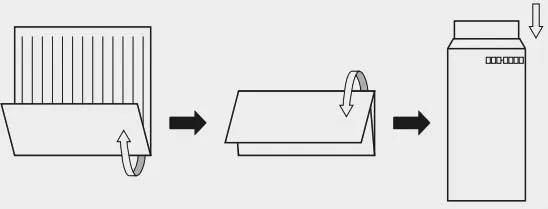
图14

尤里为了尽可能把信折叠整齐，不得不让老师教他找三等分点的方法。

老师：①找到距离相同的4条平行的直线，使信纸长边的两个端点分别放在第1条和第4条直线上；②第2条、第3条直线与信纸长边的交点为该边的三等分点。

图15

尤里：因为是4条距离相同的平行直线，于是直线与直线之间被分成了3部分，所以才能找到三等分点。

信纸一共有13条距离相同的平行直线。尤里为了找到信纸的三等分点，考虑过使用另一张纸，如图16所示，使其两端分别放在第1条和第13条直线上，就能找到三等分点了。

图16

（2）13条直线与信纸长边相交的点里有该边的三等分点，这两个点分别在哪两条直线上呢？写出答案。

3.利用橡皮筋拉动一辆小汽车。

如图17，用橡皮筋连接汽车和发射台，拉动汽车，拉长橡皮筋，然后松开，车子就会前进。我们研究当汽车头被橡皮筋分别拉到图中A位置和B位置时，发射之后汽车分别前进多少。

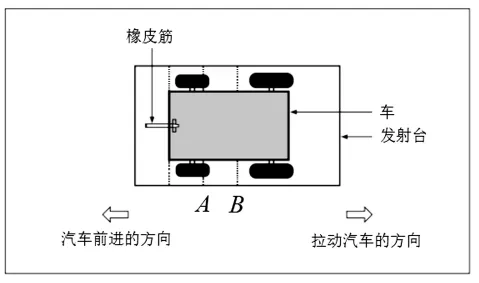
图17

首先，记录5次当汽车头被橡皮筋拉动到A位置时汽车行驶的距离，结果如表4所示。根据表4，思考汽车行驶的平均距离是多少。

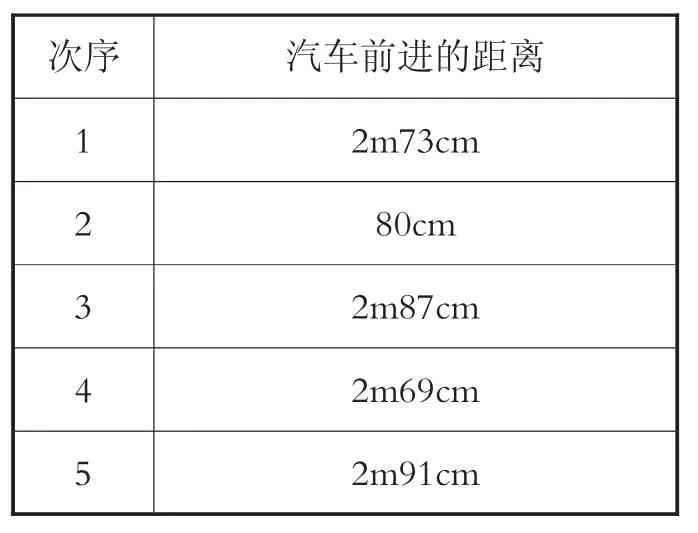
表4 被橡皮筋拉到A位置时的情况记录表

和仔：其中第2次记录，汽车路线偏离得太多，记录无法正确进行。因此，我们计算平均值时要去掉第2条记录。

（1）去掉第2条记录后，用4次的记录找出汽车平均行驶了多少厘米。下面选项中，你能找出是哪个式子吗？

其次，记录5次当汽车头被橡皮筋拉动到B位置时汽车行驶的距离，结果如表5所示。根据表5，思考汽车行驶的平均距离是多少。

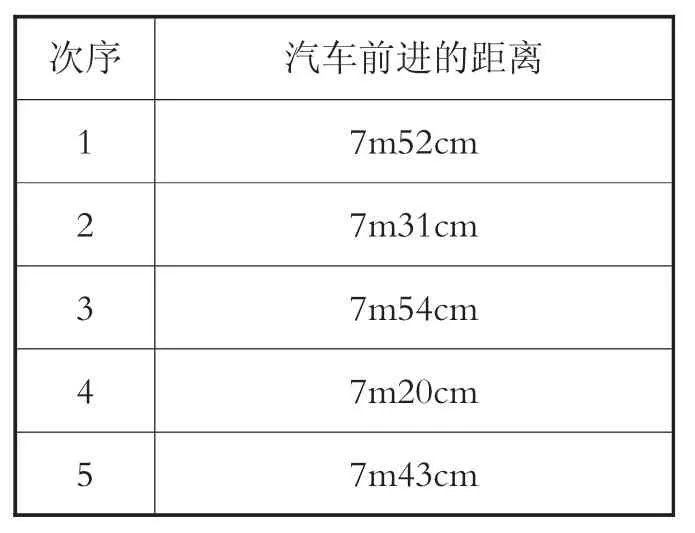
表5 被橡皮筋拉到B位置时的情况记录表

和仔为了简化平均值的计算方法，把重点放在7m后面的部分，再得到平均值，如下：

7m后面部分的平均值的求法：（52+31+54+20+43）÷5=40（cm）。

除去7m，求得平均值为40cm。

汽车行驶的平均值为7m40cm。

春菜听到和仔求平均值的方法，思考如下：

可以把重点放在7m20cm后面的部分，而不是7m后面的部分，也可以求得平均值。

（2）按照求7m20cm后面部分的平均值的方法，写出文字和表达式。

4.研究学校里四年级以上（包括四年级）学生带手帕和纸巾的情况。

榆次总结的调查结果如表6：

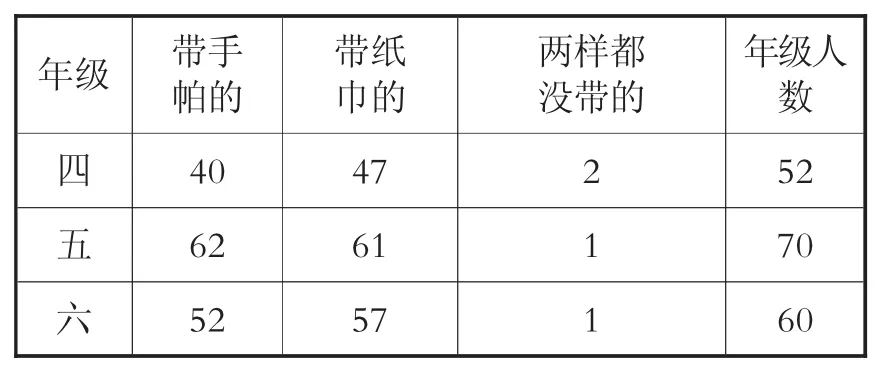
表6 带手帕和纸巾的人数

小樱：在榆次的表中，没有写出手帕和纸巾两样都带了的人数。

小樱认为要修改这个表，求出手帕和纸巾两样都带了的人数。

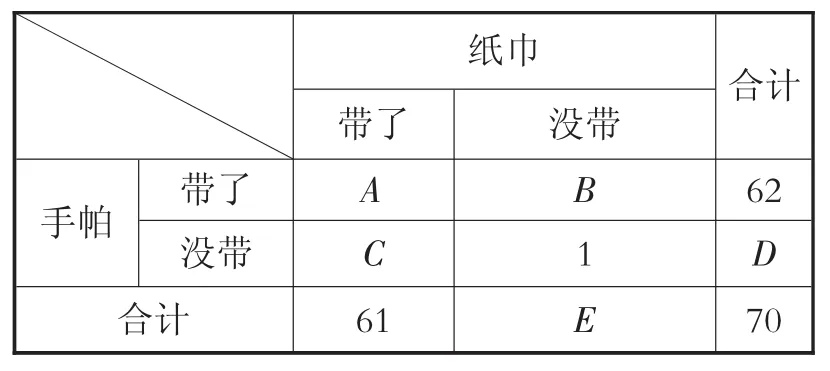
表7 五年级学生带手帕和纸巾的调查结果

小樱根据表格列出以下式子，求得手帕和纸巾两样都带了的五年级学生的人数为54，如下：

在小樱列出的式子中，“9”是没带纸巾的合计总人数，所以这个“9”应填在表7中的E处。

（1）在小樱列出的式子中，“8”是表7中什么的人数？写出文字答案。另外，这个“8”应该在表7中的哪个位置？

榆次：我想创建一个图表，展现各年级学生带手帕和纸巾的情况。

小樱：因为各年级的人数不同，我认为如果创建图表展现“各年级人数”与“手帕和纸巾都没带的人数”之间的比例关系，也是一件好事。

（2）如果把“各年级的人数”与“手帕和纸巾都没带的人数”之间的比例关系用图表展现出来，请从①～④（如图18～21）中选出最合适的一个图表。

图18

图19

图20

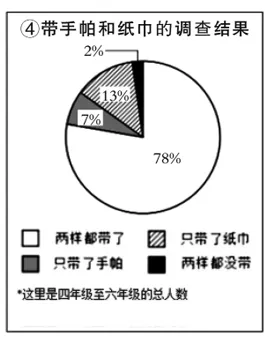
图21

5.月亮在围绕地球旋转的同时，与地球的距离也在发生变化，时远时近，但月球本身的大小并没有改变。离地球远时看起来小，离地球近时看起来大。满月时所见到的最大月亮的直径称为“最大满月直径”，最小月亮的直径称为“最小满月直径”。“最大满月直径”比“最小满月直径”大14%。

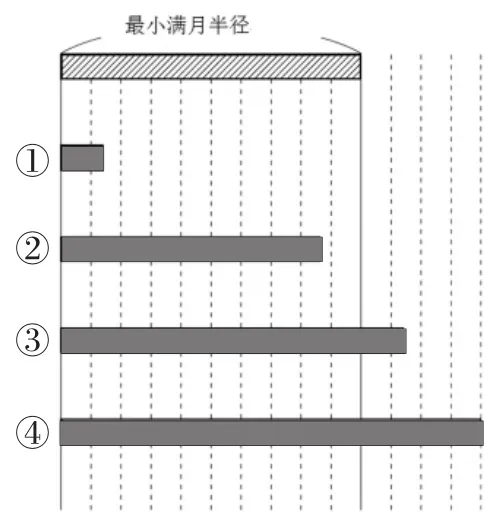
图22

思考月亮的直径和硬币的直径。

1日元、100日元、500日元硬币直径分别是20mm、22.6mm、26.5mm。

（2）将“最小满月直径”视为1日元的硬币直径，那么“最大满月直径”与100日元、500日元中哪一个硬币的直径更接近？写出理由。