沟通联系合理选择纵深伸展——“解决问题的策略”总复习建议

◇高 敏

“解决问题的策略”学习贯穿了小学阶段的学习全过程。从总复习的角度来说，建议从“整理与反思”和“练习与实践”两个方面展开，从而让学生体会不同策略的优势，合理进行策略的选择，提高策略应用的水平，增强主动应用策略分析和解决问题的自觉性。

一、整理与反思：打通知与思的障碍，内化完善

在“解决问题的策略”学习中，学生寻求和确定解决问题的方案是关键。新授时的学习往往只侧重教学某一种解决问题的策略，通过复习与整理，可以将以往所学的知识融在一起，连成一片。

1.知识整理，让思考有据可依。

为了让学生整体、系统地梳理知识，形成良好的认知结构，“知识整理”环节至关重要。“回顾解决问题的一般步骤，想一想：在解决问题的过程中，我们经常用到的策略有哪些？各有什么特点？它们之间有什么联系？并尝试举例说一说。”以此唤醒学生的记忆（如图1和图2）。

图1

图2

2.回顾与反思，让思考有“悟”可感。

反思是数学思维活动的核心。在解决问题的过程中，组织学生进行回顾和反思，有助于学生把解决问题过程中的感性经验提升为理性的认识，有助于改变学生只关心解题结果、不关心为什么这样做的习惯性思维方式，突出了解决问题过程本身的价值。可以说，没有真正的反思，也就没有真正意义上的策略的生成。

例：周大伯把一块长方形地分成两部分，分别种植黄瓜和番茄（如图3)。种黄瓜的面积比种番茄的面积少180平方米，黄瓜和番茄各种了多少平方米？

图3

学生对解决问题的过程进行了回顾与反思。针对学生的想法，教师组织学生进行了交流。

生1：可以利用画图的策略，在图中画出番茄地中和黄瓜地完全相同的一块（如图4），这样180÷20=9（米），番茄地的面积是（30+9）×20÷2=390（平方米），黄瓜地的面积是390-180=210（平方米）。

图4

生2：假设番茄地的面积为x平方米,那么黄瓜地的面积就是（x-180）平方米,两块地的面积之和是30×20平方米，然后我列出了x+(x-180)=30×20，只要解方程就可以解决问题。

生3：180平方米是两块地的面积差，整个长方形的面积30×20平方米是两块地的面积之和，想到了用解决“和差问题”的方法解决这道题。

生4：我觉得做完后回过头来检验一下很有必要，我把求到的结果当作条件算出390+210=600（平方米），390-210=180（平方米），与题中的两个已知条件给出的数据完全一致，我对自己的答案充满信心。

在回顾与反思中，有的是对自己解题过程的回顾，有的是对自己方法的说明，有的是对策略选择经验的感悟，有的是如何进行检验……使得复习教学更好地实现了从“学什么，学到了什么”到“怎样学，为什么这样学”的深度学习。

需要特别说明的是，策略贵在运用，运用重在选取。策略的形式有很多，各有特点，又各具优势，在反思中可以彰显其独特的价值。

例：①有《美食启东》《好玩的数学》《全景电影》三个微信公众号，分别每两天、三天、四天更新一次。某月1日三个微信公众号同时更新后，到这个月15日，哪几天没有微信更新？哪一天三个微信同时更新？

②小强、小华、小东是好朋友。他们互相发一封电子邮件，一共要发多少封电子邮件？

在讨论中，学生明显感到第①题用列表的方法更清晰、有效，第②题用画图连线整理优势更明显。在完成题目的过程中，学生深刻感受到策略需要选取，它们有各自适用的情境，虽有联系，但各具特点，在反思中感悟不同策略的优越性。

二、练习与实践：打通理与练的联系，融会贯通

整理可以使知识结构系统化，但这种结构化的知识是否具有旺盛的生命力，还要看能否被学生合理、有效地运用于新问题的解决过程中。

1.多样中见一致。

总复习阶段，要防止大题量的机械训练，要多运用一题多变、一题多解等形式，逐步有序地展开。

例：①小可和小乐共有72元零用钱，小乐比小可多12元，两人各有多少元？

②小可和小乐共有72元零用钱，小乐给小可12元，两人的零用钱就同样多，两人各有多少元？

③小可和小乐共有72元零用钱，小乐给小可12元后还比小可多2元，两人各有多少元？

④小可和小乐共有72元零用钱，小乐的零用钱是小可的2倍，两人各有多少元？

这五道题中，无论是相差关系还是倍数关系，在不断变化的过程中，“小可的钱+小乐的钱＝72元”这一数量关系始终不变。学生在“变”的现象中发现“不变”的本质，从“不变”的本质中探究“变”的规律，使分析问题的策略更有条理，解决问题时也就游刃有余了。

2.简约中孕丰富。

策略的复习不只是一种知识的复习，也不只是熟练解决某一类题目，获得某一类问题的结论，更为重要的是将解决问题的策略内化为学生自己的数学素养。

例：用16根1米长的木条靠墙围一块长方形菜地，怎样围面积最大？小组合作，用16根木条围一围，算一算，把结果填入表1。

表1

如果用24根这样的木条来围，怎样围面积最大？

受这道题的启发，我设计了如下的题组：

①用24根1米长的木条围一块长方形菜地，有哪些不同的围法？怎样围面积最大？

②用24根1米长的木条靠墙围一块长方形菜地，有哪些不同的围法？怎样围面积最大？

③用24个1平方厘米的小正方形拼成一个长方形，有哪些不同的拼法？怎样拼周长最小？

解决这三道题都可以使用一一列举的策略，其中第①题中24是四条边的长，所以根据“长＋宽＝24÷2”列举，再组织学生思考：周长一定，怎样围面积最大？进行比较后可以得出：周长相等的长方形，长和宽相等（即是正方形）时面积最大。进而类推出“和相等的两个数，差越小，积越大”这样具有数学模型性质的结论。

第②题也是已知周长围长方形，与第①题的区别在于：24是三条边的长，所以根据“长＋2个宽＝24”列举。通过比较得出：一边靠墙时，当长是宽的2倍时，面积最大（实际上是围成了两个正方形）。

第③题与上面两题不同，是已知面积拼长方形，所以根据“长×宽＝24”列举，再组织学生探寻规律：面积一定，怎样拼周长最小？

学生做了多少道题不重要，重要的是做题后的自我总结、领悟。如果方法背后没有思想，那么方法不过是一种笨拙的工具。解决问题的策略不仅仅对应的是某种具体的方法，更重要的是要关注背后蕴含的数学思想。

3.错误中现主动。

很多学生对复习课不感兴趣，原因是教师对学生的学习基础及学习需求了解得不够多。在复习课上，教师应及时捕捉信息，在练习题的选择上用足心思，如学生平时作业中的常错题、学生单元测试卷中的常错题……了解学生存在哪些知识漏洞和能力缺陷，从而对症下药。

例：在数位表（如表2）上摆圆片表示数：10个○，能摆出几个数呢？

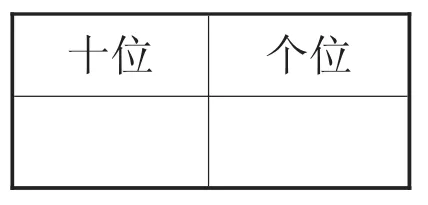
表2

学生摆：

1个○：1、10 共2个数

2个○：2、11、20 共3个数

3个○：3、12、21、30 共 4个数

4个○：4、13、22、31、40 共 5个数

5个○：5、14、23、32、41、50 共 6个数

……

师：想一想，10个○呢？

生：（大多数脱口而出）11个数。

生：我不同意，10个○不能全部放在个位，也不能全部放在十位，所以应该减少2个，只能摆9个数。

脱口而出的答案代表一种习惯性思维，在“补救”的过程中，“错误”带给学生的是更主动、更深入、更细致的思考。

策略是一种特殊的智慧。有的放矢地进行复习，向思维深处渗透，必能使学生在原有能力的基础上获得提高，得到发展。