具源项和阻尼项发展方程整体吸引子的Hausdorff维数
2018-08-02张媛媛
张媛媛
(开封大学 数学教研部,河南 开封 475000)
具源项和阻尼项的发展方程整体吸引子的性质是近年来偏微分方程研究的热点,目前关于它的研究主要集中在其存在性及维数方面.文献[1-3]对方程
utt-div{σ(|u|2)u}-Δut+Δ2u+h(ut)+g(u)=f(x)
的整体吸引子及分形维数做了相关研究.文献[4]对该方程的Hausdorff维数做了相关讨论.文献[5-7]对一些非线性发展方程解的长时间行为也做了相关论述.论文的目的是研究下列一类具源项和阻尼项的发展方程整体吸引子的Hausdorff维数问题.方程中牵涉到的非线性项一直是偏微分方程处理的难点,对非线性源项和阻尼项的先验估计更是复杂与繁琐,估计时可能不易控制.这里将采取算子半群与偏微分方程中常用不等式结合的方法,对方程中的4个非线性项作估计,尽可能地减少复杂的运算,也使估计更精确,有
(1)
(2)
u(x,0)=u0(x),ut(x,0)=u1(x),x∈Ω,
(3)
其中:Ω是RN中具有光滑边界的有界区域.笔者采取半群的方法研究方程(1)整体吸引子的维数,这在相关文献中还没有出现过.
1 相关引理及主要结论
记
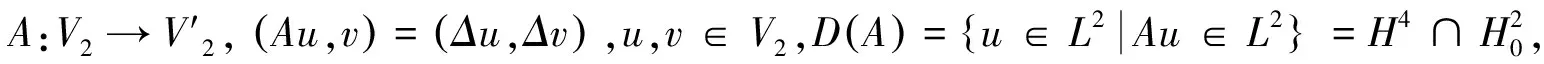
定义As(s∈R),Hilbert空间
考虑问题(1)~(3)的Cauchy问题
(4)
u(x,0)=u0(x),ut(x,0)=u1(x).
(5)
引理1假定下列条件成立
(1)
(2)f=h1+h2,hi:V1→V-1,i=1,2,h(s)s≥0,‖h2(v)‖V-1≤C(h2(v),v)1-σ2,
‖h1(v)‖V-1≤C(1+(h2(v),v))1-σ3,
(3) ∃σ4,σ5∈(0,1),δ1,δ2∈(0,2δ),有
‖g(u)‖V2δ-1≤C(R)(1+‖u‖V2(1+δ))1-σ4,u∈V2(1+δ),‖u‖V2≤R,
‖h(v)‖V2δ-1≤C(R)(1+‖v‖V1+2δ)1-σ5,v∈V1+2δ,‖v‖≤R,
‖g(u1)-g(u2)‖V2δ-1≤C(R)‖u1-u2‖V1+2δ1,u1,u2∈V1+2δ,‖u1‖V1+2δ+‖u2‖V1+2δ≤R,
‖h(v1)-h(v2)‖V2δ-1≤C(R)‖v1-v2‖V1+2δ2,v1,v2∈V1+2δ,‖v1‖V2δ+‖v2‖V2δ≤R.
(4)βi∈C1(R),βi(s)s≥B1|s|α+2,|βi(s)|≤B2(1+|s|α+1).
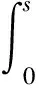
(6) (u0,u1)∈X2+2δ.
引理2[10]设X,Y是Banach空间,X⊂Y.若φ∈L∞(0,T;X)∩Cw([0,T];Y),则φ∈Cw([0,T];X).
引理3[11]设X是Hilbert空间.B⊂X是紧集,S:B→X是连续映射,S(B)=B,若下列条件成立
(1)S在B上一致可微.即∀u∈B,存在线性算子L(u)∈L(X),使得


则dH(B) 引理4[12]设X是Hilbert空间,q(t;.),r(t;.)是X上的二次型,{L(t)|t∈[0,T),0 (1) ∀η0∈X,q(t;L(t)η0)绝对连续,且∀t∈[0,T),q′(t;L(t)η0)=r(t;L(t)η0); 注1定义S(t)(u0,u1)=(u(t),ut(t)),则S(t)组成X2+2δ中的连续半群. 注2在定理1的假定下,注1定义的连续半群在X2+2δ上存在整体吸引子. 定理1假定引理1的条件成立,且满足下列条件 (1) (3)σi,βi∈C2(R). 则注2中的整体吸引子存在Hausdorff维数. 引理5若定理1中的条件(1),(2)成立,则∀R>0,∃σ0:0<σ0<<1,(u,v)∈X2+2δ,则 ‖g′(u)‖L(V2+2δ-σ0,V2δ-2)≤C(R),∀u∈V2+2δ,‖u‖V2+2δ≤R, ‖f′(v)‖L(V2δ,V2δ-1)≤C(R),∀v∈V2δ,‖v‖V2δ≤R. 引理6若定理1中的条件(1),(2)成立,则∃0<γ<<1,且 ∀ξ,η∈V2+2δ,‖ξ‖V2+2δ+‖η‖V2+2δ≤R, 第一步: 变分方程解的存在性. (6) v(0)=v0,vt(0)=v1. 其中 (v0,v1)∈X2+2δ. (7) (6) 式与Aδvt作内积,得 (8) (9) (10) 由引理5,有 (11) (12) 由(8)~(12)式,得 (13) 由假定不难得估计 ‖vtt‖L2(0,T;V2δ-2)≤C(R,T),t∈[0,T]. (14) 在X2+2δ中(n→∞),有 (15) (15)式令n→∞,对t求导,由ωj在V2中的稠密性得(6)式,v是问题(6)~(7)的解,且 v∈L∞(0,T;V2+2δ),vt∈L∞(0,T;V2δ)∩L2(0,T;V1+2δ),vtt∈L2(0,T;V2δ-2), 所以,由引理2,有v∈Cw([0,T];V2+2δ).同理,(v,vt)∈Cw([0,T];X2+2δ). (8)式在(t0,t)上积分,当t→t0时,得 所以,(v,vt)∈C(R+;X2+2δ). 第二步:S(t)在Α上一致可微. 设L(t,φ0):X2+2δ→X2+2δ,L(t,φ0)(ξ,η)=(v,vt),φ0∈A,则L(t,φ0)=DS(t)φ0. 则 所以,S(t)在X2+2δ的有界集上Lipschitz连续. 上式与Aδψt作内积,得 (16) 又 (17) (18) (19) 将(17)~(19)式代入(16)式,得 由Gronwall不等式, 得 (20) 再令θ=ψ-v,θ满足 (21) θ(0)=0,θt(0)=0, 其中:F=g1+g2+g3+g4,且 将(21)式与Aδθt作内积,得 (g′(u)θ,Aδθt)-(f′(ut)θt,Aδθt)+(F,Aδθt), (22) (23) (24) 由引理6,有 (25) (26) (27) (28) 将(23)~(28)式代入(22)式,得 由(20)式和Gronwall不等式,有 第三步:Α的Hausdorff维数. 令ω=vt+εv,(6)式转化为 上式与Aδω作内积,得 (29) 其中 将以上4式代入(29)式, 得 令K:X2+2δ→X2+2δ,K{u,v}=A-σ{u,v},{u,v}∈X2+2δ,有 (30) 其中 ∃α,β>0,使得 设L1(t,φ0):X2+2δ→X2+2δ,L1(t,φ0)ψ0=ψ(t),其中 则 其中 (30)式亦可写为 当m>m0时,由引理4,有 由引理3,有 dimHΑ≤m0<∞. 证毕.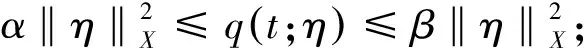



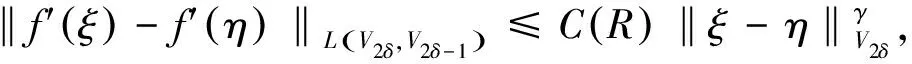
2 定理1的证明





