基于线性光学系统的 W 态融合研究进展
2018-08-02王洪福
韩 雪,王洪福
(1.哈尔滨工业大学 理学院 物理系,黑龙江 哈尔滨 150001; 2.延边大学 理学院 物理系,吉林 延吉 133002)
纠缠是量子信息处理的重要资源,在实际量子信息处理中,不仅需要两体纠缠态(Bell态),也需要大尺度的纠缠态.由于W态对抗比特损失是鲁棒的(即测量W态中一个粒子时其余粒子仍处于纠缠),因此制备大尺度的W态成为热点.拓展和融合是制备大尺度W态的有效方案.拓展方案能在已有的1个n粒子W态上每次增加2个粒子来扩大W态的尺度.与拓展方案相比,融合方案更加高效,它可以一次性融合2个大尺度的W态而得到一个更大尺度的W态.如图1所示,Alice和Bob手中分别有2个大尺度W态|Wn〉A和|Wm〉B,从|Wn〉A和|Wm〉B中各发送1个粒子至融合装置,只有发送至装置的粒子参与融合,其余粒子作为常数保留在Alice和Bob处.经过一系列操作后,对参与融合的2粒子中的一个进行测量,另一个发回原来的装置,继续进行大尺度的W态融合.测量得到2种结果:一种是得到2个较小尺度的W态,它们继续发送至相同装置重复上述的融合过程,直至粒子数小于2,融合终止;另一种是实现了大尺度的W态融合,得到了更大尺度的W态|Wn+m-1〉.
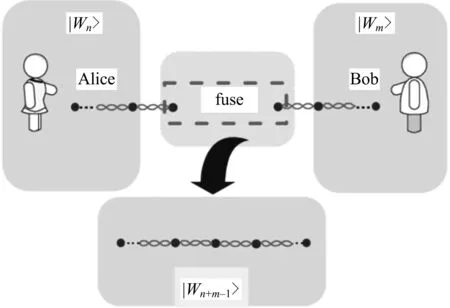
图1 融合过程示意图
近年来,研究人员相继提出不少W态融合方案[1-12].2011年,Özdemir等[4]首次利用线性光学提出融合门,融合1个n比特的W态及1个m比特的W态,生成1个(m+n-2)比特的W态,因此通过融合操作不仅扩大了W态的尺度,而且纠缠资源也得到了充分利用.2013年,Bugu等[5]在文献[4]的基础上作了改进,在1个Fredkin门和1个单光子的辅助下,实现了(n+m-1)比特的W态融合.Yesilyurt等[6]利用3个controlled-NOT门和1个Tooli门,融合m,n,t,z比特的W态,生成(n+m+t+z-4)比特的W态.2014年,Özaydin等[7]用辅助单光子以及1个Fredkin门,融合m,n,t比特的W态,生成1个(n+m+t-1)比特的W态.值得注意的是,上述方案均利用了多比特受控门,如CNOT,Tooli,Fredkin门,然而实验上实现这些受控门有很大困难[13].笔者简要综述几类W态融合方案,并着重阐述弱交叉克尔非线性系统和量子点-微腔耦合系统中不借助受控相位门,实现W态融合的方案及其物理原理,最后给出总结与展望.
1 基于弱交叉克尔非线性系统的W态融合
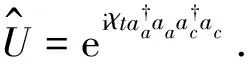
(1)
从(1)式可以看出,通过弱克尔介质非线性作用后,信号模没有发生改变,而探测模的相干态相位被调制,相位角的改变量恰好与信号模的光子数成正比.通过探测相干态的相位变化,可以计算出信号模中的光子数,并且不破坏信号模的光子,因此通过弱交叉克尔介质可实现非破坏性光子数测量.
图2为文献[4-5,8]的融合方案对比,其中虚框表示融合机制.图2A方案中,融合后两个光子均被探测器探测到.图2B方案中,通过引入1个Fredkin门和1个辅助单光子,实现了(n+m-1)比特的W态.图2C方案中,仅需探测1个光子,而另1个光子发回参与融合的原来的态中,在不需要辅助光子的情况下,可获得(n+m-1)比特的W态,不仅减少了资源消耗,还可以利用Bell态制备3比特W态.
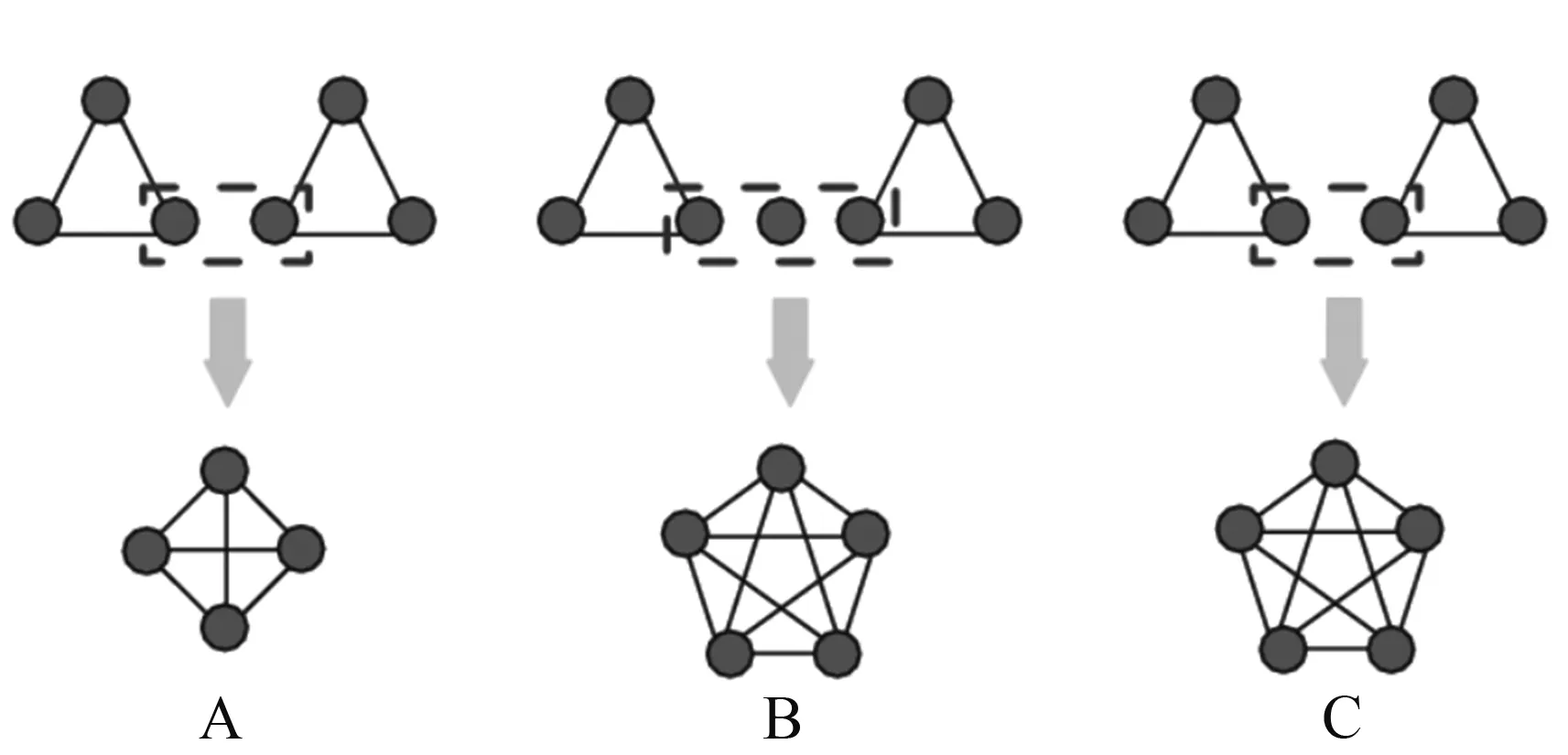
图2 文献[4](A),[5](B),[8](C)的融合方案对比
基于弱交叉克尔非线性系统的W态融合方案[8]如图3所示.
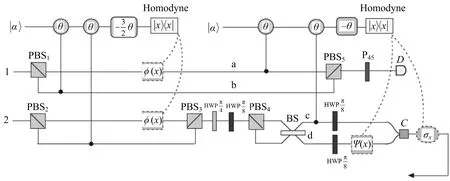
图3 基于弱交叉克尔非线性系统的W态融合方案
Alice和Bob的W态分别为
(2)
整个系统初态为
|a〉|1V〉1|1V〉2+|b〉|1H〉1|1V〉2+|c〉|1V〉1|1H〉2+|d〉|1H〉1|1H〉2.
(3)
只有模1,2的光子发至融合装置,处于模a,b的剩余的光子将被保留在Alice,Bob处.光子经过PBS和弱交叉克尔介质后,在相干态上执行一个-3θ/2相移操作,执行第1次零差测量[16-18],再经过一系列线性光学元件,最后执行第2次零差测量.当探测器D探测到光子时,整个系统态变为
|Φ〉=|a〉|1V〉2+|b〉|1H〉2+|c〉|1H〉2=
(4)
可见,最终得到了尺度为(n+m-1)的光子W态.
2 基于量子点-微腔耦合系统的W态融合
对于InAs/GaAs自组织量子点[19],当量子点受到光激发后,价带上的电子会吸收一个光子从价带跃迁到导带,这样导带中多了一个电子,而价带中留下一个空穴,通过库仑相互作用形成一个电子-空穴对(即激子)[20].根据泡利不相容原理,带电激子的跃迁过程与过剩电子的状态有关.带电量子点的能级结构如图4所示.
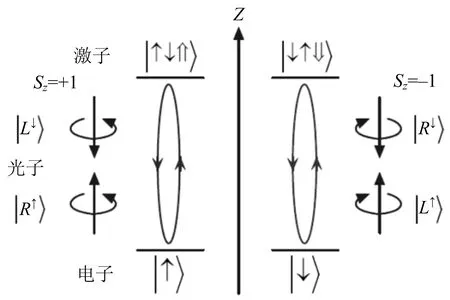
图4 带电量子点的能级结构
嵌入微腔的带电量子点相当于一个2能级量子系统.将其嵌入双边腔,根据量子点光激发选择定则和双边腔的反射透射特性,可以得到
|R↑,↑〉→|L↓,↑〉,|L↑,↑〉→-|L↑,↑〉,
|R↓,↑〉→-|R↓,↑〉,|L↓,↑〉→|R↑,↑〉,
|R↑,↓〉→-|R↑,↓〉,|L↑,↓〉→|R↓,↓〉,
|R↓,↓〉→|L↑,↓〉,|L↓,↓〉→-|L↓,↓〉.
(5)
(5)式广泛应用于量子信息处理[21-25].
2.1 电子比特的W态融合方案
基于量子点-微腔耦合系统(n+m-1)电子比特的W态融合方案[9]原理如图5所示.
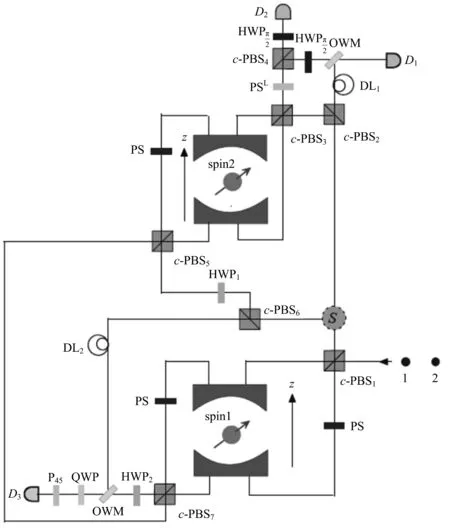
图5 基于量子点-微腔耦合系统(n+m-1)电子比特的W态融合方案原理图
图5中,spin1和spin2均为量子点-微腔耦合系统,c-PBSi(i=1,2,3,…)为椭圆基矢极化分束器,HWPi为半波片,QWP为1/4波片,S为光学开关,PS为π相移器,DLi为时间延迟装置,Di为光子探测器.
Alice和Bob的W态分别为
(6)
整个系统初态为
|Φ0〉=|Wn〉A⊗|Wm〉B⊗|R1〉⊗|R2〉=
(|a〉|↑〉1+|b〉|↓〉1)⊗(|c〉|↑〉2+|d〉|↓〉2)|R1〉|R2〉.
(7)
首先让光子1进入腔1,光子的|L1〉,|R1〉部分分别完成(c-PBS1→|L1〉→PS→spin1→c-PBS1)和(c-PBS1→|R1〉→spin 1→PS→c-PBS1)操作,随后光子1的|L1〉部分进入腔2与电子自旋2作用,|L1〉部分经历(c-PBS2→c-PBS3→spin 2→PS→c-PBS4→HWPπ)这些操作后,变为(|b〉|c〉|R1〉|↓〉1|↑〉2+|b〉|d〉|L1〉|↓〉1|↓〉2)⊗|R2〉.|R1〉部分不与腔2中的电子自旋2作用.当探测器探测到光子时,系统态为
|Φ2〉=(|a〉|c〉|R1〉|↑〉1|↑〉2+|a〉|d〉|R1〉|↑〉1|↓〉2+
|b〉|c〉|R1〉|↓〉1|↑〉2+|b〉|d〉|L1〉|↓〉1|↓〉2)⊗|R2〉.
(8)
显然,当探测器D2探测到光子,此态变为|b〉|d〉|↓〉1|↓〉2⊗|R2〉,此时得到两个分离的小尺度的W态|Wn-1〉和|Wm-1〉,随后它们将使用相同机制继续融合.当探测器D1探测到光子时,系统态变为
|φ1〉=(|a〉|c〉|↑〉1|↑〉2+|a〉|d〉|↑〉1|↓〉2+|b〉|c〉|↓〉1|↑〉2)⊗|R2〉.
(9)
|φ1〉将继续参与下面的融合过程.
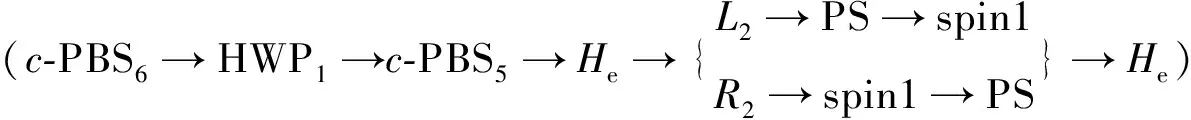
|φ2〉=|↑〉1(|a〉|c〉|↑〉2+|a〉|d〉|↓〉2+|b〉|c〉|↓〉2).
(10)
很明显,电子自旋1与其他电子自旋已经解纠缠了,此时其余的电子自旋可表示为
|φ3〉=|a〉|c〉|↑〉2+|a〉|d〉|↓〉2+|b〉|c〉|↓〉2=
(11)
由式(11)知,|φ3〉是尺度为(n+m-1)的电子W态|Wn+m-1〉,获得这个W态相应的概率为(n+m-1)/nm.
2.2 光子比特的W态融合方案
基于量子点-微腔耦合系统中(m+n-1)光子比特的W态融合方案[9]的原理如图6所示.图6中所有光学元件与图5的相同.
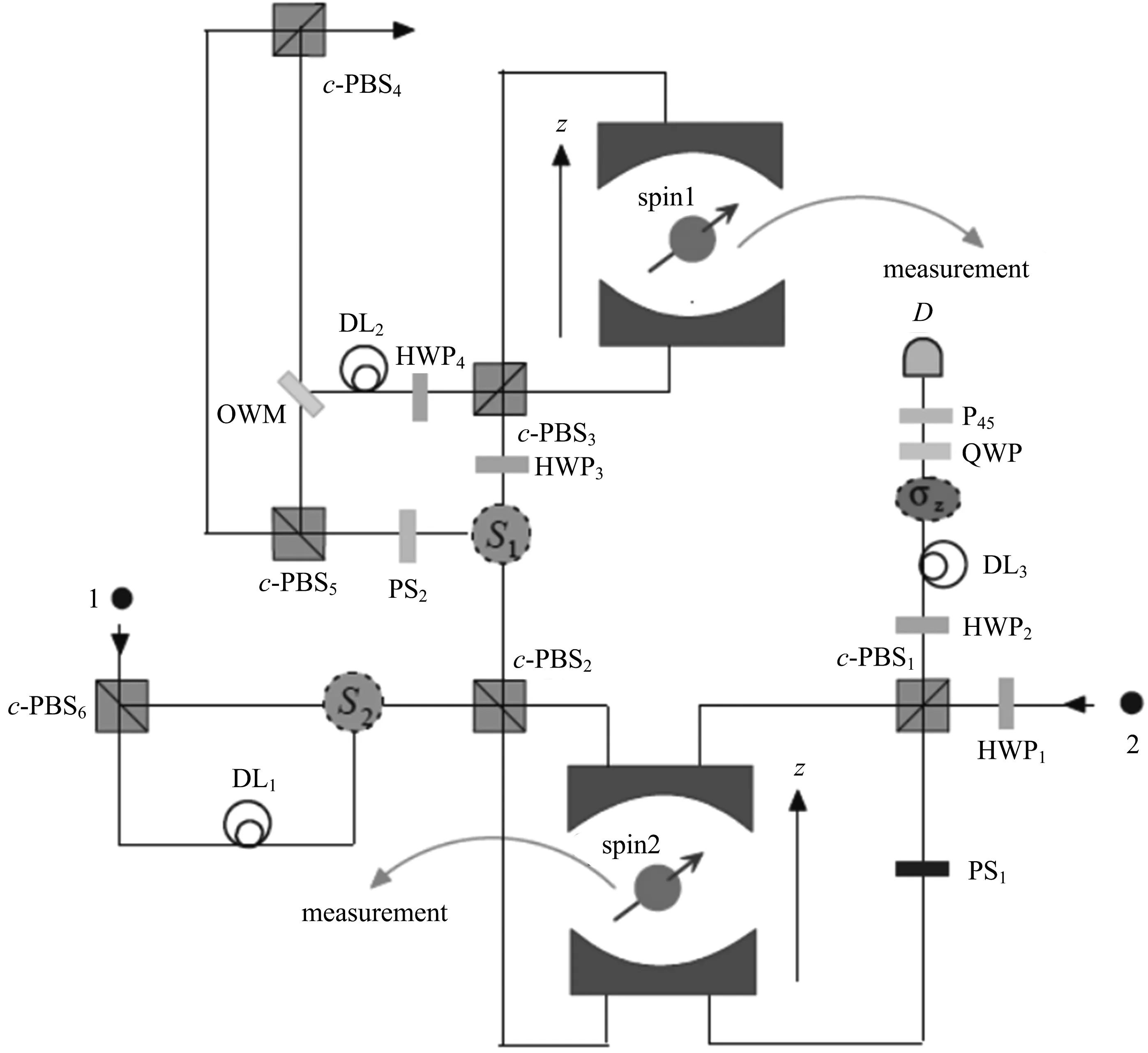
图6 基于量子点-微腔耦合系统中(m+n-1)光子比特的W态融合方案原理图
Alice和Bob的W态分别为
(12)
(13)
|Ψ1〉=|↑〉1(|a〉|c〉|R〉1|R〉2|↑〉2+|a〉|d〉|R〉1|L〉2|↓〉2+
|b〉|c〉|L〉1|R〉2|↓〉2)-|b〉|d〉|R〉1|L〉2|↓〉1|↓〉2.
(14)
对电子自旋1执行测量,有下面2种测量结果
|↓〉1:|ψ1〉=-|b〉|d〉|R〉1|L〉2|↓〉2,
|↑〉1:|ψ2〉=|a〉|c〉|R〉1|R〉2|↑〉2+|a〉|d〉|R〉1|L〉2|↓〉2+|b〉|c〉|L〉1|R〉2|↑〉2.
(15)
对电子自旋|↓〉1的结果,将获得2个小比特数的W态|Wn-1〉和|Wm-1〉,这2个小尺度的W态能通过相同融合机制继续循环,最终得到较大尺度的W态.对电子自旋|↑〉1的结果,探测到的态将继续用于之后的融合.处于延时器DL1的光子1的|R1〉部分经过S2,c-PBS2进入腔2,|R1〉部分执行(c-PBS2→spin 2→c-PBS2→S1→PS2→c-PBS5→OWM)操作.
对电子自旋2执行一个Hadamard门,且在基矢{|↑〉,|↓〉}下测量,若测量结果为|↑〉,则系统剩余态变为
|Ψ2〉=|a〉|c〉|R〉1|R〉2+|a〉|d〉|L〉1|L〉2+|b〉|c〉|L〉1|R〉2.
(16)
随后,光子2依次通过QWP,P45.当光子探测器D探测到光子时,剩余态为
|Ψ3〉=|a〉|c〉|R〉1+|a〉|d〉|L〉1+|b〉|c〉|L〉1=
(17)
由式(17)知,|Ψ3〉为尺度为(n+m-1)的光子W态|Wn+m-1〉.若电子自旋2是处在|↓〉,态|Wn+m-1〉变为
|Ψ4〉=|a〉|c〉|R〉1|R〉2-|a〉|d〉|L〉1|L〉2+|b〉|c〉|L〉1|R〉2,
(18)
此时,只要在光子2通过QWP之前执行一个σz操作,光子态就变为|Ψ2〉.重复上述操作,最终获得的|Ψ4〉为|Wn+m-1〉,相应的成功概率为(n+m-1)/nm.
3 总结及展望
近年来提出的W态融合方案中,大部分是在复杂的多比特控制门的基础上提出的,而目前复杂的多比特控制门在实验上实现难度较大.该综述对W态的融合研究进行介绍,并着重阐述弱交叉克尔非线性系统和量子点-微腔耦合系统中无需借助受控相位门实现W态的融合方案.当前的研究多数聚焦于基于弱交叉克尔非线性系统和量子点-微腔耦合系统的W态融合方案,这些融合方案是否能推广到更广泛的量子系统(如金刚石氮空穴中心与微腔耦合系统、腔光力系统等)是今后探索的方向.
