“含参”题复习用力点：重视运算化简的训练——一道“含参”考题解析与微教学设计

☉江苏省张家港市梁丰初级中学 于景秋

近年来随着大家对“伪函数”考题（以函数图象为背景，实质考查的是几何基本图形的繁难构造与推理证明）的批判，一类含参数的压轴题渐渐成为不少地区的命题热点，这类考题抽象、晦涩，考生往往止步于草图构造，含多个参数的运算与变形，使得不少学生面对这类问题常常感到无从下手，这就需要老师们精心构思，自己先要加深对这类考题的理解程度，然后再设计铺垫式问题带领学生深度参与、学会解题.本文结合某地区的一道中考模考的含参压轴题，先给出思路突破，再跟进教学微设计，提供研讨.

一、考题与思路突破

考题 如图1，抛物线y=ax2+bx（a＞0，b＜0）交x轴于O，A两点，顶点为B.

（1）直接写出A，B两点的坐标（用含a，b的代数式表示）；

（2）直线y=kx+m（k＞0）过点B，且与抛物线交于另一点D（点D与点A不重合），交y轴于点C，过点D作DE⊥x轴于点E，连接AB，CE，求证：CE∥AB；

（3）在（2）的条件下，连接OB，当∠OBA=120°，时，求的取值范围.

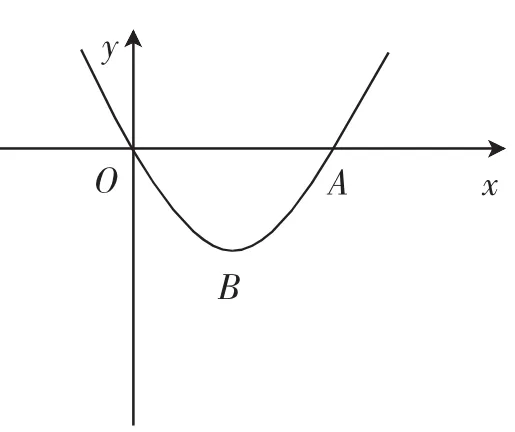
图1

（2）先构造可能的草图分析（如图2或图3），过点B作BF⊥OA于F点.接下来明确解题目标（求解方向），待证的AB∥CE，只要求出这两条直线与x轴形成的同位角相等（∠FAB=∠OEC）即可.而这组同位角恰在两个直角三角形（Rt△ABF，Rt△OCE）中，只要能证明两个直角三角形相似或者这两个同位角的三角函数值相等都可实现问题的解决.由（1）中B，结合a＞0，b＜0，k＞0的已知条件，可得，所以在Rt△ABF中，tan∠FAB=-.

图2

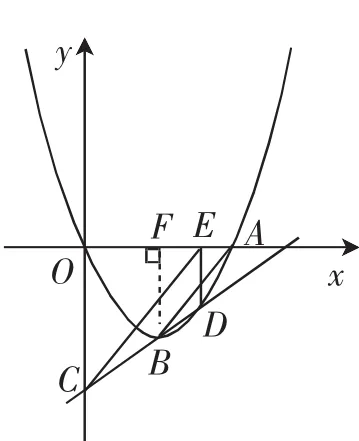
图3

所以tan∠FAB=tan∠OEC，所以∠FAB=∠OEC，即AB∥CE.

图4

至此转向对另一个条件“∠OBA=120°”的解读，如图4，在Rt△ABF中，tan∠BAF=tan30°=，而前面（2）中已求tan∠BAF=-.于是-，解出b=-.

解后反思：本题主要难点在于含参的运算、变形，如在第（2）问中，用含3个参数的式子求出直线与y轴交点坐标另外将直线与抛物线联立求出交点D的横坐标也是关键步骤.这些含多个参数式子不但在第（2）问是重要进展，在第（3）问求线段比值也需要，对含参数的运算变形提出了很高的要求.

二、解题教学微设计

教学环节（一）基础热身

例1 如图1，抛物线y=ax2+bx（a＞0，b＜0）交x轴于O，A两点，顶点为B.

（1）当OA=2时，直接写出抛物线的对称轴方程；

（2）求A，B两点的坐标（用含a，b的代数式表示）；

（3）连接AB，当b=4时，求tan∠BAO的值；

（4）若△AOB是等边三角形，求b的值.

设计意图：第（1）问先感受抛物线对称轴与OA的关系；第（3）问为后面问题（原考题第（2）问）设计铺垫、热身；第（4）问对应着原考题第（3）问“∠OBA=120°”.此环节不仅可以满足所有学生的需求，还可以为后续的活动铺垫，起到承上启下、激发学生兴趣的效果.

教学环节（二）抬级而上

例2 如图2，抛物线y=ax2+bx（a＞0，b＜0）交x轴于O，A两点，顶点为B.直线y=kx+m（k＞0）过点B，且与抛物线交于另一点D（点D与点A不重合），交y轴于点C.过点D作DE⊥x轴于点E，连接AB，CE.

（1）求tan∠BAO的值（用含b的代数式表示）；

（2）求点C的坐标（用含a，b，k的代数式表示）；

（3）求点E的坐标（用含a，b，k的代数式表示）；

（4）求证：CD∥AB.

设计意图：前面3问都是为第（4）问设计的铺垫式问题，结合（2）（3）问学生就可以想到求tan∠OEC的值.此问旨在渐进式提升，一方面对前面的问题进行巩固与变式、拓展与提升，另一方面开启学生新的思维征途，满足学生更高层面的发展需要.

教学环节（三）挑战难题

例3 题干部分同“例2”.连接OB，且∠OBA=120°.

（1）求b的值；

设计意图：为了学生能顺利解决最后一问，设计了两个铺垫问题.这两个问题从广度和深度上进一步满足学生发展与提升的需要.

教学环节（四）变式再练

变式题 如图5，直线y=kx（k＞0）与抛物线y=ax2（a＞0，b＜0）交于O，A两点.

（1）直接写出A点的坐标（用含a，k的代数式表示）；

（2）直线y=b（b＞0）交抛

物线于C，B两点，过B作BD⊥x轴，交直线y=kx于D点，过点A作AE⊥x轴于E点，连接OC，DE，判断直线OC与DE的位置关系，并说明理由.

设计意图：变式不仅是一种有效的巩固，更是一种有效的拓展与提升，其不仅可以考查学生对知识与技能的掌握深度，还能激发学生进一步发散思维，拓展思维宽度和广度.

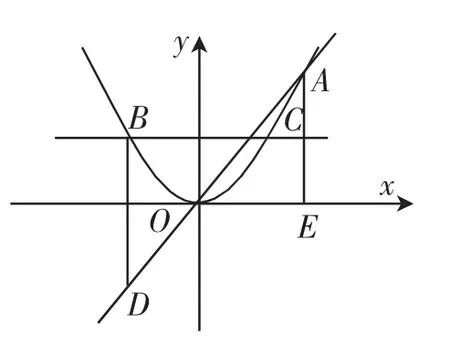
图5

三、进一步的思考

第一，加强含参题教学研究，重视含参运算能力训练

随着命题风向与热点的转移，含参考题是不少地区中考复习训练的重要任务.如何提升这类考题的教学效果？我们不能盲目地以题海战术来取胜，而应该将含参考题进行分解，逐个击破.一般来说，多参数问题总体解答方向都是需要通过较为繁杂的运算来实现“消参”的目的.特别是，学生对含参运算普遍感觉吃力，这时就需要安排小专题复习，训练含参数的方程或整式、分式的变形与化简或求值.

第二，精心预设铺垫式问题，助力学生自主发现思路

对于较难的含参考题往往第（2）、（3）问之间拉开较大距离，这里学生不容易找到台阶、发现铺垫，或者是对某一个条件的忽略与无视，以致没有思路.这里解题教学时，要在这些学生易忽略、难解析的条件上设置铺垫，让学生充分解读这些条件的价值与可能带来的图形位置或某参数的值.值得一说的是，不少学生关于解题方向的明确也是值得训练的，有些题的设问非常隐蔽，“言东而指西”，需要认真解读、转化设问，明确真正的解题目标.像本文中考题最后一问，解析目标实质上是分析出

在应试教育制度背景下，我们的教学离不开题目的训练与检测，但是，如果我们深入分析教学内容的价值，锁定习题的方向与价值，不断的实践和优化习题的价值，将知识与技能与数学的学科价值相融合，开启核心素养落地生根的新征途，笔纸化考查制度将会插上素质教育的双翅，飞得更高、更远.