认知无线电网络同步交会算法研究∗
2018-07-31李晓艳
李晓艳 华 翔 张 勇
(西安工业大学电子信息工程学院 西安 710021)
1 引言
在认知无线电网络中,根据网络的拓扑结构,认知网络可以分为集中式网络和分布式网络[1~3]。在集中式网络中,一个中心基站控制着网络中所有的节点,并协调网络资源的分配。在分布式网络中,由于缺少中心基站的支持,次用户间进行数据传输之前需要使用公共控制信道CCC来交换彼此的控制信息[4~5],如何设计和选择 CCC 是分布式认知网络频谱共享的核心问题。以跳频序列的方式实现动态的CCC是目前研究最为活跃的频谱共享方式。
以跳频序列的方式实现动态的CCC是指次用户跟随一种特定的跳频序列接入到它的所有可用信道中,并在此过程中实现与其他次用户的交会[6~8]。当次用户对在相同的时间接入到相同的信道时,它们可以在此共同信道上交换彼此的控制信息,这即是交会。交会算法用来产生跳频序列,并且必须保证有共同可用信道的任意两个次用户之间能够实现交会。
针对网络中节点时钟同步的情况下,文献[9]最早提出了一种交会算法,称为SYN算法。该算法首先将系统时间划分为等长度的N个时隙,N是认知网络中的总信道数量,将这N个时隙依次分配给N个信道;节点在其可用信道对应的时隙上广播它的相关信息,邻居节点监听到该信息之后对其信道信息进行存储,以便在合适的时隙进行通信。这个算法要求节点有两个收发器,而且需要通信的节点对必须等到协商好的通信信道对应的时隙到来的时候,才能进行通信。文献[10]提出了一种采用请求集的交会算法,称为QCH算法。该算法将网络中所有信道集合看做是一个请求集系统,将可用信道按照请求集的结构安排到跳频序列对应的时隙中。QCH算法的基本跳频序列长度为L=N2,且这个算法可以保证任意两个节点间的交会能在一个有限的交会时间(Time to Rendezvous,TTR)内达到。文献[11]提出了一种被称为DH的交会算法;在此算法中,跳频序列由三个参数确定,即初始信道、跳频种子和切换种子。DH算法的基本跳频序列长度为L=N2+2N,该算法也提供了一个有限的TTR,但是必须要求网络中总的信道数量N是一个素数。QCH算法和DH算法均要求网络中的所有节点感知到相同的空闲频谱集合,这大大限制了交会算法的应用场景。
针对以上几种算法存在的问题,本文提出了一种基于请求集的同步交会算法,称为SRA(Synchro⁃nous Rendezvous Algorithm)算法。在SRA算法中,节点的跳频序列仅由节点感知到的可用信道决定,即节点间的跳频序列可以相同也可以不相同。只要节点间包含一个共同可用信道,本算法就能保证它们可以在一个基本跳频序列周期内实现交会,而不关心节点间是否感知到相同的可用信道集合,且对于网络中总的信道数量也没有任何要求。除此之外,本算法提供了一个有限的TTR,且相比较于QCH算法和DH算法,本算法具有最短的基本跳频序列长度。
2 系统模型
考虑一个带有 n={0,…,N-1}个信道和m={1,…,M}个次用户的认知无线电网络,每个次用户装有一个半双工的收发器,在通信范围之内且在同一个信道上的次用户对可以相互通信。为简便起见,后文中“次用户”和“节点”交替使用。
假设系统时间被划分为相同长度的时隙ΔL,每个时隙足够长以至于节点可以交换多个数据包。以 Si表示第 i (i=1,…,M)个节点感知到的空闲频谱集合,节点的跳频序列由一个基本跳频序列重复构成,节点跟随它的跳频序列接入到可用信道中 。基本 跳 频序列 为 X={ x0, x1,...xL-1} ,长度为L,其中 xj表示节点在第 j个时隙接入到xj信道中。
3 请求集理论
下面简要介绍文献[12~13]中的请求集理论。
定义1 给定一个普通集合U={0,…,K-1},K为自然数,一个请求集系统Q是集合U下的一个非空子集,Q中的每个元素称为一个请求集,且请求集之间满足以下的相交特性:
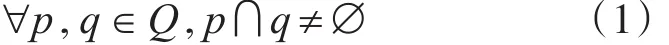
定义2 给定一个非负的整数i和一个请求集p,定义 p的旋转请求集为

定义3 请求集系统Q被称为具有旋转相交特性,如果它其中的请求集满足

例 如 ,Q={ {0,1}, {2,0}, {1,2}} 是 一 个 在U={0,1,2}下的请求集系统,含有3个请求集。任取其中2个请求集,{0,1}和{1,2},交集为{1}。以请求集q={0,1}为例,带有2个元素,以标签s标示,图1所示为请求集q与它的两个旋转请求集。
从图1可以得出,q的两个旋转请求集为rotate (q,1)={1,2} 和 rotate (q,2)={2,0} 。同理可得出Q的其余2个请求集的旋转请求集,这些请求集和旋转请求集满足定义3,则Q具有旋转相交性。

图1 一个请求集和它的旋转请求集
4 同步交会算法
利用请求集理论,将认知网络中的n={0,…, N-1}个信道看作是一个集合U ,每个节点感知到的空闲频谱集合作为一个请求集。如果任意两个节点的空闲频谱集合有交集,则称这两个节点属于相同的请求集系统。通过本文的同步交会算法,使得属于同一请求集系统的节点能够发生交会。接下来,定义几个与同步交会算法相关的概念。
定义4 给定一个信道集合n={0,…,N-1} (N≥3),设存在三个正整数 P ,r和 c。 P 是大于或等于N的最小非素数,且这三个整数满足如下的条件:

根据定义4,在本文的同步交会算法中,设置一个基本跳频序列由c个子序列组成,每个子序列包含N个时隙,这N个时隙的序号为{0,1 ,…, N-1} 。从上式(3)~(4)可知,当 c 满足 c(mod 2)≠ 0 时,可以表示为本跳频序列的长度为
定义5 给定一个信道总数N,一个交会矩阵R是一个以行为主的r×c矩阵,将这N个信道依次安排到矩阵R中,即任意一个信道n, n∈[0,N-1],在 R 中都有相应的位置 (d,g),且
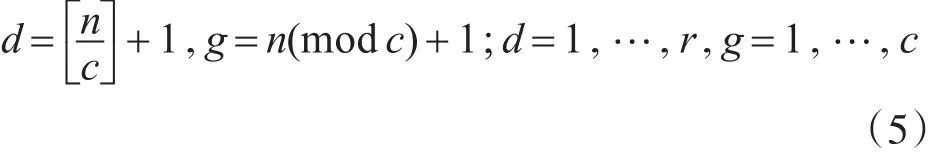
例如,联合以上定义4和5,给定 N=4,则有P=r×c=2×3,交会矩阵为
定义6 给定一个交会矩阵R和一个节点的空闲频谱集合S;对比集合S,将矩阵R中不属于集合S的信道去掉,以下两条规则用于调整矩阵R中剩余信道的位置:
1)在某一列中,如果有一行的信道被移除了,把下一行的信道提到这个空缺的位置。
2)如果某一列的所有信道都被移除,则把变量h指定到该列。变量h表示随机的从集合S中选择一个信道。
在R中的剩余信道经过位置调整之后,组成一个新的矩阵,称为子交会矩阵SR。
根据以上定义以及请求集理论,本文提出了一种同步的交会算法用于产生节点的跳频序列,所提算法描述如下:
步骤1:对于一个给定的信道总数N,交会矩阵R和基本跳频序列的长度L可以确定;根据交会矩阵R和节点的空闲频谱集合S,子交会矩阵SR也可以确定。
步骤2:将S看作为一个请求集。对比集合S,寻找基本跳频序列的各个子序列中时隙序号等于S中信道的时隙,把这些时隙称为请求时隙;而子序列中剩余的时隙称为普通时隙。
步骤3:将矩阵SR中第i列的信道安排到基本跳频序列第i个子序列的请求时隙中,i∈[1,c]。在此过程中,如果有两个或两个以上的信道存在于矩阵SR的同一列中,则如下的附加规则可以用于安排信道:
1)把信道安排到时隙序号与它的值相同的请求时隙中;
2)把具有偶数值的信道安排到时隙序号是偶数的请求时隙中,反之亦然。
步骤4:对于每个子序列上的普通时隙,随机的从集合S中选择信道安排其中。
接下来举例说明本算法如何产生跳频序列。给定 N={0 ,1,2,3,4},则有个基本跳频序列的长度L=N×c=15。给定三个节点的空闲频谱集合 SA={0,1,2,4},SB={2,3, 4},SC={1,2,3,4}。由于三个节点的空闲频谱集合有交集,则这三个节点属于同一个请求集系统,通过本算法设计的跳频序列可以使得三个节点必然发生交会。从定义6可以得到。对于节点 A 而言,每个子序列中编号为{0 ,1,2,4}的时隙即是请求时隙,其余的就是普通时隙,如图2所示。

图2 子序列中的请求时隙和普通时隙
根据SRA,将信道0和2分别安排到在第一个和第三个子序列的请求时隙中;当考虑第二个子序列时,由于SRA的第二列有两个信道1和4存在,因此使用附加规则来安排信道。根据附加规则(a),将信道1和4分别安排到时隙序号为{1}和{4}的请求时隙中;然后再根据附加规则(b),将信道4安排到时隙序号为{0,2}的请求时隙中。最后,从SA中任意选取信道安排到三个子序列的普通时隙中。同理,按照算法可以安排其余两个节点B和C的基本跳频序列,结果如图3所示(对任意两个节点,只选择了一个时隙来表示交会情形)。从图3可以看出,在一个基本跳频序列周期内,任意两个节点可以在其共同可用信道上发生交会。
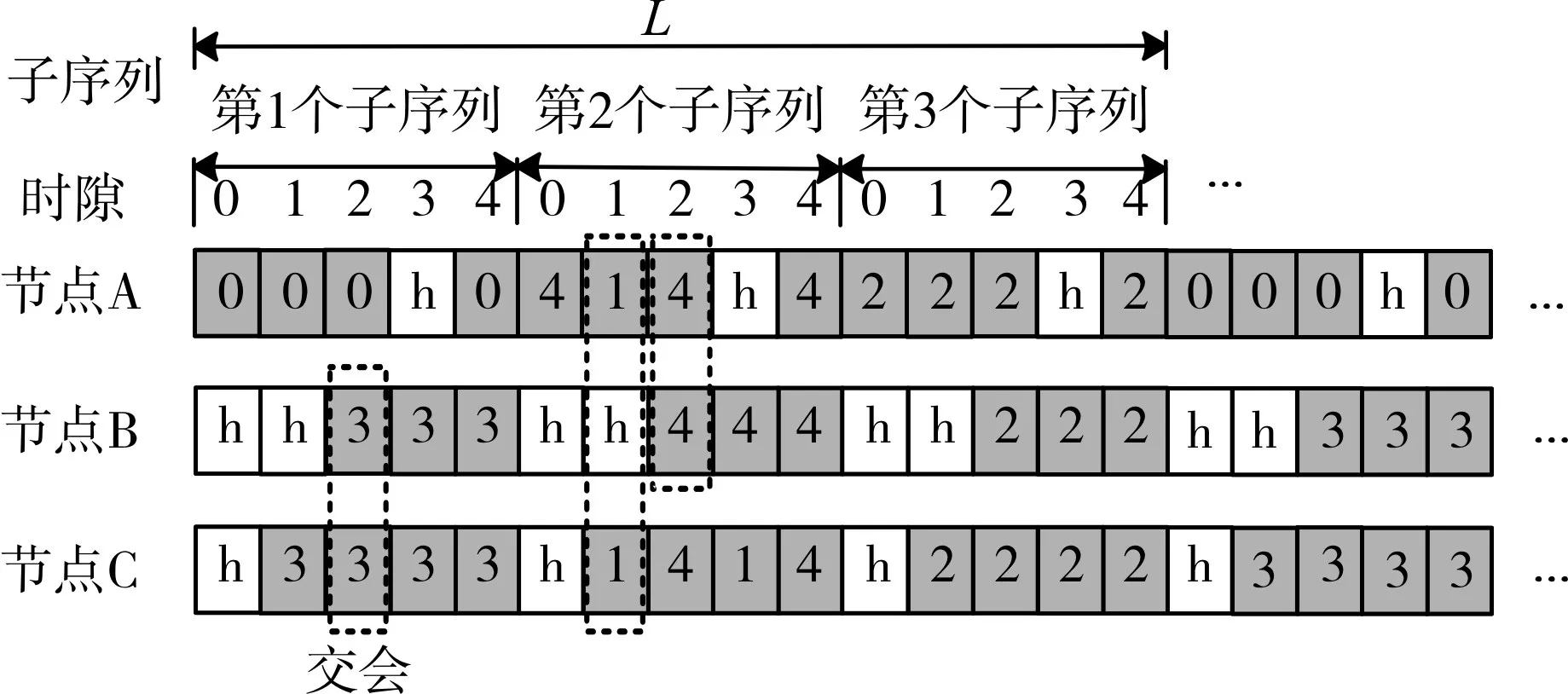
图3 同步算法的举例
5 仿真分析
为了验证所提算法的正确性和有效性,采用Matlab将本文的SRA算法与其他两个算法进行性能比较:1)QCH 算法[10],2)DH 算法[11]。在 QCH 算法和DH算法中,待基本跳频序列产生之后,节点将被主用户占用的信道从序列中移除。本文采用两个常用于评估交会算法性能的重要指标来对三个算法进行比较:平均交会时间、交会成功率[15]。
仿真参数设置为:随机放置30个次用户节点到100m×100m的区域中,次用户之间的通信距离为20 m,网络中总的信道数量为N=10,设定网络中主用户数量最大为9,主用户之间的通信距离为40 m,主用户随机地接入到任一信道中,且在任意时刻至少有一个信道被主用户对占用。网络中的时间被划分为相同长度的时隙,每个时隙长为10ms。网络中所有次用户均采用本文第二章所述的双支路检测算法进行空闲频谱检测。为了使得性能曲线更加平稳,共进行1000次独立的实验。
图4所示为认知网络中主用户数量的变化对平均交会时间的影响。对于这三个算法而言,当主用户数量增加的时候,次用户的可用信道减少,从而导致交会时间增加。反过来,当空闲信道增多时,节点需要较少的时间就能实现交会。对比三个算法,由于本算法具有最短的基本跳频序列长度,因此可以得到最少的平均交会时间。
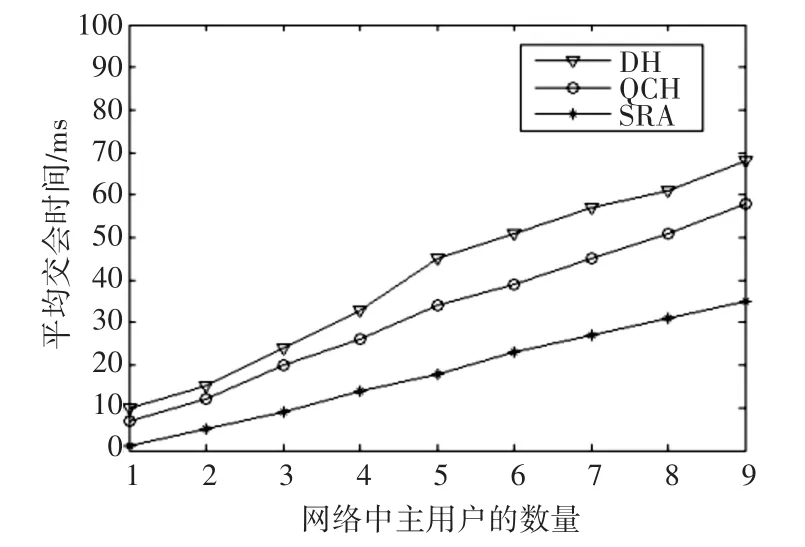
图4 主用户数量的变化对平均交会时间的影响
图5 所示为主用户数量的变化对交会成功率的影响。交会成功率定义为成功实现交会的节点对与期望实现交会的节点对之间的比值[14]。由于本文的同步算法可以保证只要次用户间存在一个共同可用信道,它们之间就可以实现交会,因此交会成功率为100%。而其余两种算法仅仅是针对当次用户节点具有相同的空闲频谱集合时的交会,当主用户数量增多时,次用户感知到的空闲频谱集合中公共信道逐渐减少,因而它们的交会成功率也逐渐下降。

图5 主用户数量的变化对交会成功率的影响
6 结语
本文为了解决同步环境下次用户之间的交会问题,特别是当次用户感知到不同的空闲频谱集合时的交会问题,基于请求集理论,本文提出了一种同步的交会算法,该算法能够保证任意两个节点之间的交会,只要两个节点间至少有一个共同可用信道。仿真结果表明,对比现有的QCH算法和DH算法,本文所提算法能够得到最低的平均交会时间,并且能达到100%的交会成功率。
