向量的线性相关性在线性方程组求解中的应用

上海电机学院数理教学部 刘美玲

向量组的线性相关性理论是线性代数课程的重要组成部分，对于线性方程组的求解有很好的辅助功能。然而本概念是该门课中最抽象、最难理解的部分之一，出于课程体系的完整性和后续学习的需要，很多学生学完了该课程，但对线性关系依然是知之甚浅，因此打击了一些学生学习该门课程的信心，丧失了对该门课程的兴趣，对后面能否求解线性方程组产生了怀疑。为此，在多年的教学实践中，必须思考如何用通俗的语言来生动形象地表达这些枯燥的概念和定理。应用类比法，则可以让学生对这些抽象概念感到熟悉、感到亲切，从而容易接受和理解。

一、线性相关性和线性方程组

线性方程组：

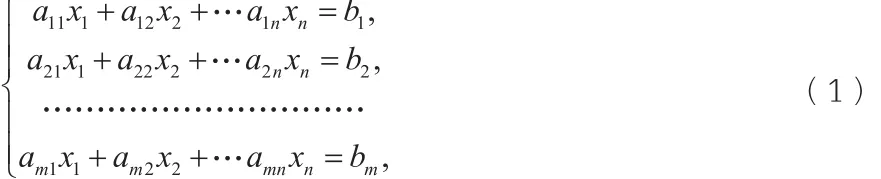
可以用向量形式表示为：

对应的齐次方程组：

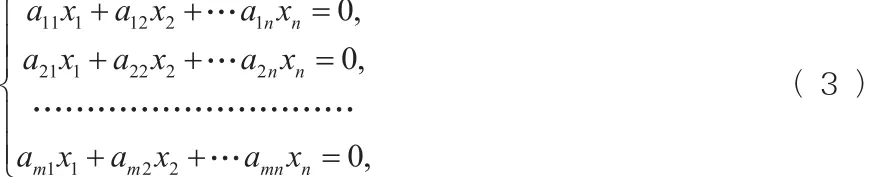
可以用向量形式表示为：

由此，方程组是否有解转变为能否找到一组数 ，使（1）式成立。

则称向量组线性相关，否则称线性无关。

由线性相关性的定义可知，对应的向量组线性相关即表示齐次线性方程组（3）有非零解；线性无关则只有零解。这里要向学生解释，方程（5）中向量组线性组合的系数 就代表方程组的解。

二、定理及举例

定理1 设向量组 线性无关，而向量组线性相关，则向量b必能由向量组A线性表示，且表示式唯一。

定理1说明线性方程组（1）有解可以表达为向量b能由向量组A线性表示，表示法唯一即表示只有唯一解。

该方程组的系数行列式

因此，方程组只有零解 ，所以向量组 线性无关。

例1题目简单明了，着重向学生讲解明白向量组合可以表示成方程组，具体显示了向量组的线性相关性和线性方程组的求解的直接关系。

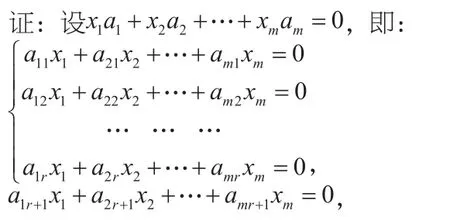
因向量组A线性无关，所以上方程组只有零解，从而B相应的方程组也只有零解，即线性无关。

定理2有些抽象难懂，讲解证明过程时充分解释将向量组合展开成方程组，即转换为了方程组的解的问题，简洁明了，生动易懂。

经过多年的教学实践证明，从调整教学内容结构、合理使用教学方法、让学生正确区分线性相关、线性表示与线性方程组的关系，注重知识的应用及结合数学软件解决实际问题，并增加应用性练习等几个方面进行教学，在提高教学质量和教学效果的同时，也教会了学生如何不断扩充自己的知识结构和体系，提高了他们的自学能力和可持续发展的能力。