Triangular temporal-distribution law for disintegrating internal solitons over a step

Dlin Tn, Jifu Zhou,*, Xu Wng

a Key Laboratory for Mechanics in Fluid Solid Coupling Systems, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190,China

b School of Engineering Sciences, University of Chinese Academy of Sciences, Beijing 100049, China

Keywords:

ABSTRACT Internal solitary waves have been found to disintegrate into a series of solitons over variable bathymetry, with important applications for offshore engineering. Considering realistic background stratification in the South China Sea, internal solitary waves propagating over a step are studied here. By assuming disintegrated solitons propagate independently, a theoretical model, namely a triangular temporal-distribution law based on the Korteweg–de Vries theory, is proposed to describe the fission process of internal solitary waves undergoing disintegration. A parameter is then introduced to quantify the accuracy of the theoretical model. The results indicate that the triangular law predicts the fission process better for a longer travelling distance and a larger amplitude of internal solitary waves.

Internal solitary waves (ISWs) are ubiquitous, and thus play an important role in the transport and dissipation of energy in the oceans. Because of the large amplitudes and strong shear currents induced by ISWs, they have a significant influence on offshore structures, biological activity and submarine navigation[1]. The propagation over a variable bathymetry can result in the dramatic deformation and disintegration of ISWs [2]. By examining the spatial characteristics of ISWs from satellite images in the South China Sea (SCS), ISWs are often observed in the form of wave packets composed of a group of rank-order ISWs on the continental shelf [3]. In spite of the considerable research into the interaction of a single ISW with offshore structures in the last decade [4-5], the impact of internal wave packets on such structures is insufficiently understood, despite being a more likely phenomenon in the oceans. This results from the fact that much remains unknown about the fission process of ISWs, especially the temporal distribution of solitons over a variable bathymetry.Here, the temporal distribution of disintegrated solitons over a step function is investigated using linear analysis and nonlinear modeling.

The Korteweg–de Vries (KdV) equation and its variants have proven to be useful nonlinear models for describing the evolution and disintegration process of ISWs in the ocean [6-7]. The disintegration of ISWs over a step is studied here in terms of a variable-coefficient KdV equation expressed as

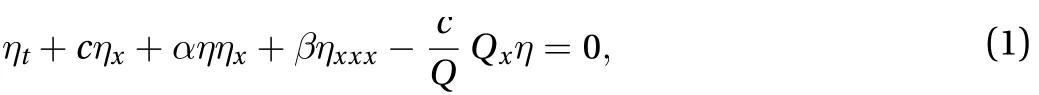
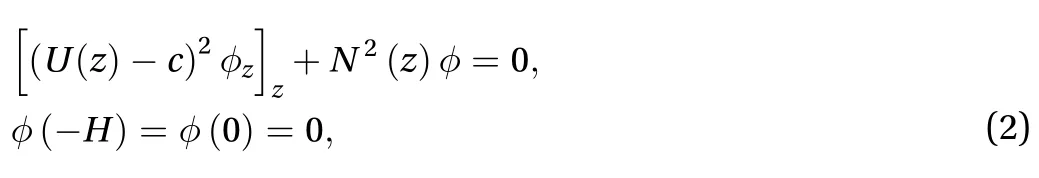
where z is the vertical coordinate with its origin at the still pycnocline, U(z) is a horizontal background shear current, N(z)is the buoyancy frequency, and H is the water depth. Here, the modal functionis normalized by its maximum value. The nonlinear coefficient, dispersive coefficient, and linear modification factor Q are given by [9]

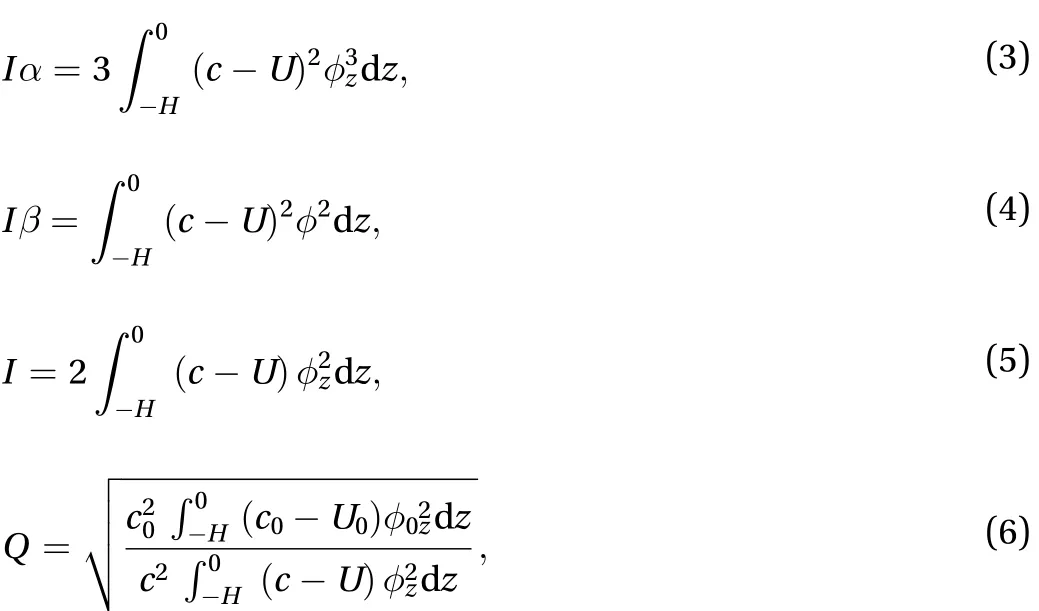
respectively, where terms with subscript 0 are evaluated at the initial position of an ISW here. To facilitate analysis, Eq. (1) is transformed to a standard KdV equation,

after introduction of the variables [6]

where s is a temporal variable, andis the wave amplitude function.

Equation (7) is first solved numerically in the transformed space with the pseudo-spectral method in s and split-step method in x. The calculated results are then transformed to the physical space using Eq. (8).

The schematic diagram of bathymetry considered here is shown in Fig. 1, where

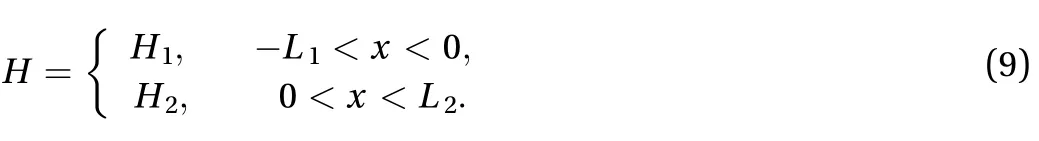
Djordjevic [10] studied an ISW travelling over a step, giving the number of disintegrated solitons and their amplitudes theoretically as

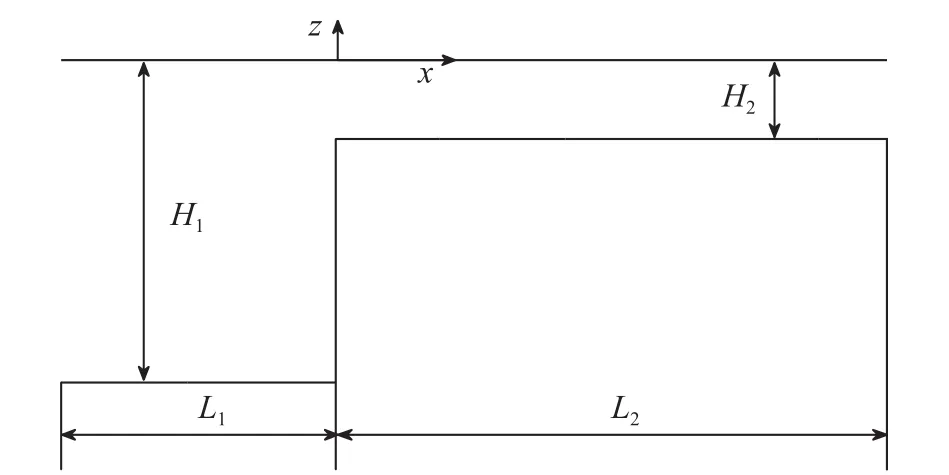
Fig. 1. Schematic diagram of the step bathymetry.

where subscripts 1 and 2 denote the coefficients in Eq. (9) before and after the step, P is the number of the total solitons, […]denotes rounding up to an integer, andis the amplitude of the n-th soliton.

The typical density in the SCS is derived from the summer climatological World Ocean Database 2013 [11]. Given H1= 3000 m and H2= 730 m, Fig. 2 illustrates the numerical fission process of an initial ISW with amplitude of 60 m disintegrating into three solitons with amplitudes of 89.9, 39.9, and 10 m. These results are in good agreement with the theoretical predictions of 90, 40,and 10 m solitons given by Eqs. (10) and (12).

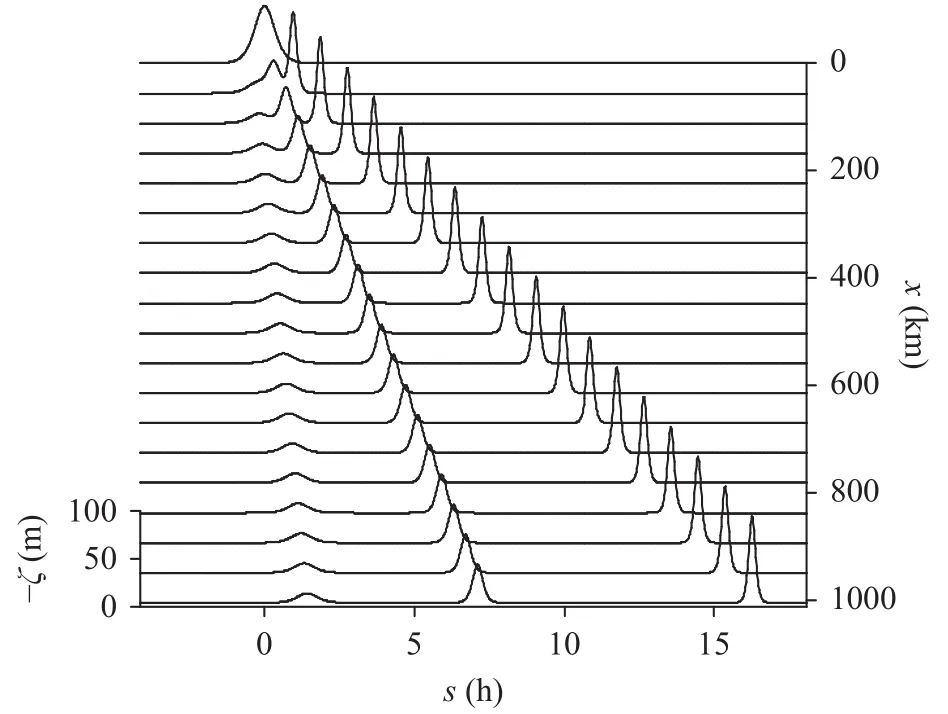
Fig. 2. The evolution of an ISW over the step.

According to Djordjevic’s theory, an ISW with initial amplitude a0propagating over a step disintegrates into P solitons with amplitudes. After the fission process is completely finished, the nonlinear interaction among solitons can be neglected. Let us, however, neglect the nonlinear interaction,even if the fission is not completely finished, so that the solitons are assumed to propagate independently. The corresponding phase speeds of these solitons, which are determined by their amplitude and the background stratification condition, are[6]. The time interval in the transformed space for the i-th and (i+1)-th solitons arriving at location x can be expressed as

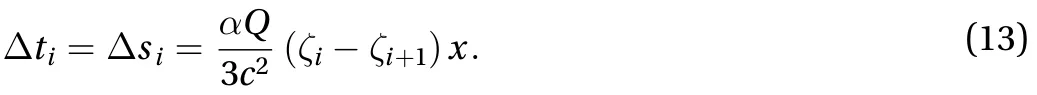
As shown in Fig. 3, the relationin the physical space at the location x.

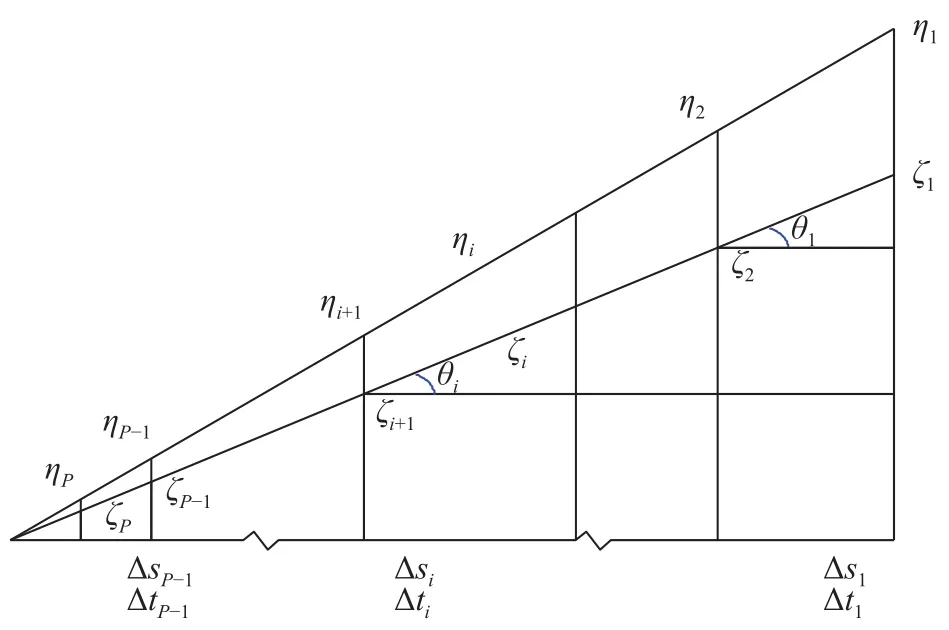
Fig. 3. Temporal distribution of solitons in a wave packet. The thick solid lines indicate the disintegrated solitons with amplitudes

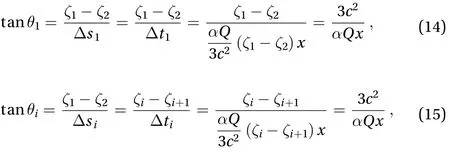
is always satisfied. Therefore, the relationis satisfied for any x, which means the temporal distribution of the amplitudes of solitons is a triangle at any location. Based on Eq. (8), the amplitude of solitons in the physical space can be expressed as

Therefore, the triangular temporal-distribution law is also suitable for the solitons in physical space.

The following parameter may be additionally determined,

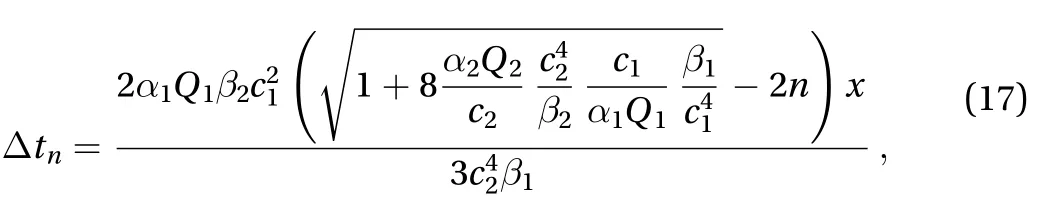
where ∆tnis the time interval for the n-th and (n+1)-th solitons arriving at location x.

Since solitons are constantly interacting with each other during the fission process, the temporal distribution of solitons is not precisely triangular as in the above theoretical model. To investigate the nonlinear interaction of the solitons, the parameter

is introduced, where i and j indicate the sequence of numbers of the studied solitons in a wave packet, and the parameter F can be used to measure the degree to which the triangular law deviates from the nonlinear fission process modeled according to KdV theory. A larger F indicates stronger nonlinear interaction of solitons, while F equals zero in the absence of any nonlinear interaction among solitons.

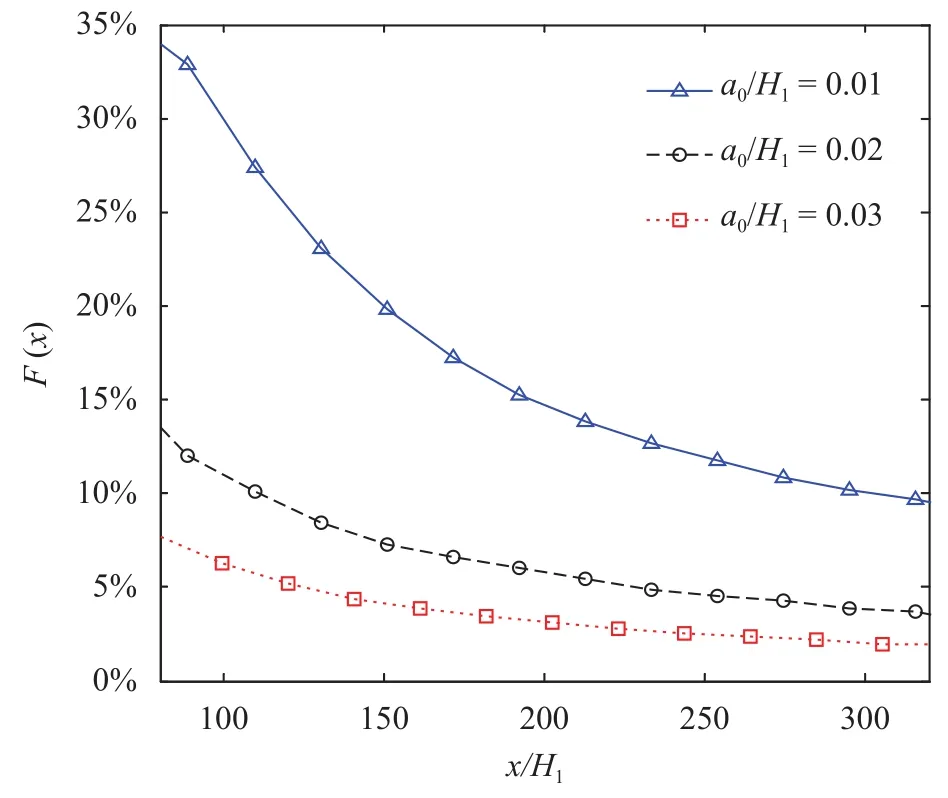
Fig. 4. Variation of the parameter F along the bathymetry for different wave amplitudes.

The variation of parameter F for i = 1 and j = 2 is shown in Fig. 4,where the horizontal coordinate and initial amplitudes are normalized by the water depth H1. On the one hand, the trend of the three curves indicates that F approaches zero as x increases,which implies that the proposed triangular law becomes more accurate for larger x or a longer time interval between solitons in the evolution process (see Eq. (13)). On the other hand, the curve with a larger amplitude of a soliton is of a smaller F value,which implies that the proposed triangular law holds more accurately for larger ISWs, since the phase speed of ISWs are proportional to their amplitudes, making solitary waves with larger initial amplitude disintegrate faster. Therefore, the nonlinear interaction of internal solitons during the fission process can be quantitatively evaluated by consideration of the proposed parameter F.

In conclusion, a triangular temporal-distribution law for disintegrating solitons over a step is proposed to approximate the fission process of ISWs governed by the nonlinear KdV equation,with the accuracy of the law defined by the proposed parameter F. Use of the law enables the prediction of soliton variation from limited field measurements, and thus is of potential significance in the research of the impact of ISWs on offshore structures.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (11572332 and 11602274), the National Key R&D Program of China (2017YFC1404202), and the Strategic Priority Research Program of the Chinese Academy of Sciences(XDB22040203).