Rational subgrid-scale modelling: a short survey
2018-07-27FngLu
L. Fng, L.P. Lu*
a LMP, Ecole Centrale de Pékin, Beihang University, Beijing 100191, China
b National Key Laboratory of Science and Technology on Aero-Engine Aero-Thermodynamics, School of Energy and Power Engineering,Beihang University, Beijing 100191, China
Keywords:
ABSTRACT We review the previous attempts of rational subgrid-scale (SGS) modelling by employing the Kolmogorov equation of filtered quantities. Aiming at explaining and solving the underlying problems in these models, we also introduce the recent methodological investigations for the rational SGS modelling technique by defining the terms of assumption and restriction. These methodological works are expected to provide instructive criterions for not only the rational SGS modelling, but also other types of SGS modelling practices.
The large-eddy simulation (LES) technique has been developed in the last half-century, leading to various subgrid-scale(SGS) models published in academic journals. The spirit of SGS modelling is to relate the SGS tensor to the grid-scale (GS)quantities [1, 2]. This relation indeed describes a very strong instant multi-scale correlation which is not physically correct and involves tight restrictions on the velocity fluctuations. In previous studies, we conclude this step by using the term “assumption” [3-6]. There are various assumptions such as the eddy-viscosity assumption [7], the scale-similarity assumption [8], the gradient diffusion assumption [9], the velocity increment assumption [10, 11], etc. For definition, we comment that an assumption assumes a (local) similarity between GS and SGS quantities.
As described above, the assumptions only assume an explicit or implicit link between GS and SGS quantities, but this link usually is not assumed in a complete expression. Instead, one or more undetermined coefficients or functions are usually required to allow involving additional mathematical or physical restrictions. From our previous studies, A restriction is a physical, mathematical, empirical or phenomenological simplification which is employed in the SGS modelling closure, such as the inviscid simplification [12], the scaling laws [13-17], the filter similarity [18], the velocity profile restriction [19], etc. There can be multiple restrictions in one SGS model. In general, the reason of choosing multiple restrictions is that we hope the generated turbulence can satisfy more physical or mathematical laws. Whereas, sometimes multiple restrictions lead to non-negligible error,which will be discussed later. We remark that according to the different methods that the restrictions are employed into SGS models, we can also define the “structural modelling” and “functional modelling” [1]. The difference between these two methods is whether the restrictions are defined to the SGS tensor itself.
The restrictions, involved in the SGS modelling procedure,can be either phenomenological or rational, according to different understandings of the turbulence statistics. A phenomenological methodology employ an external restriction which is statistically observed in turbulent flows or simplified mathematical models, but are usually not direct conclusions from the Navier-Stokes equations; by contrast, a rational methodology aims at derive all restrictions analytically starting from the Navier-Stokes equations and the Kolmogorov-Obukov theories, which are usually regarded as traditional foundations in turbulence research history. It is not easy to insist on the rational methodology since quite few analytical relations can be found without external phenomenology. In this contribution we then review a series of attempts on rationally understanding the SGS modelling procedure, based on the Kolmogorov equation of filtered quantities(KEF) which is usually considered as an exact physical law in turbulent investigations.
The first work considering the KEF as a necessary physical condition can be found in Ref. [20]. Starting from this idea, the KEF was used as a restriction in SGS modelling and yields many rational SGS models in different flow contexts.
The Cui-Zhou-Zhang-Shao (CZZS) model [12] might be the first attempt using the KEF to rational formulate an SGS model.This model is based on the traditional eddy-viscosity assumption and derived under the conditions of homogeneity and isotropy. Due to the eddy-viscosity assumption, it is an eddy-viscosity SGS model, while different extensions to other assumptions were discussed in Ref. [21]. Calculations in both homogeneous isotropic turbulence (HIT) and channel turbulence show a posteriori improvements. However, there are still unclear points in this work. For example, in Ref. [12] two formulations of CZZS model are proposed, one in which corresponds to dynamically determined model coefficient, while the other one corresponds to constant coefficient using the scaling law. In Ref. [13] it was shown that the dynamically determined coefficient always leads to divergence. As shown in Fig. 1, the dynamically determined model coefficient always yield numerical energy accumulation at high wavenumbers and lead to divergence, while the fixed resolved-scale scaling law leads to stable runs. The discussion on this phenomenon will be shown later.
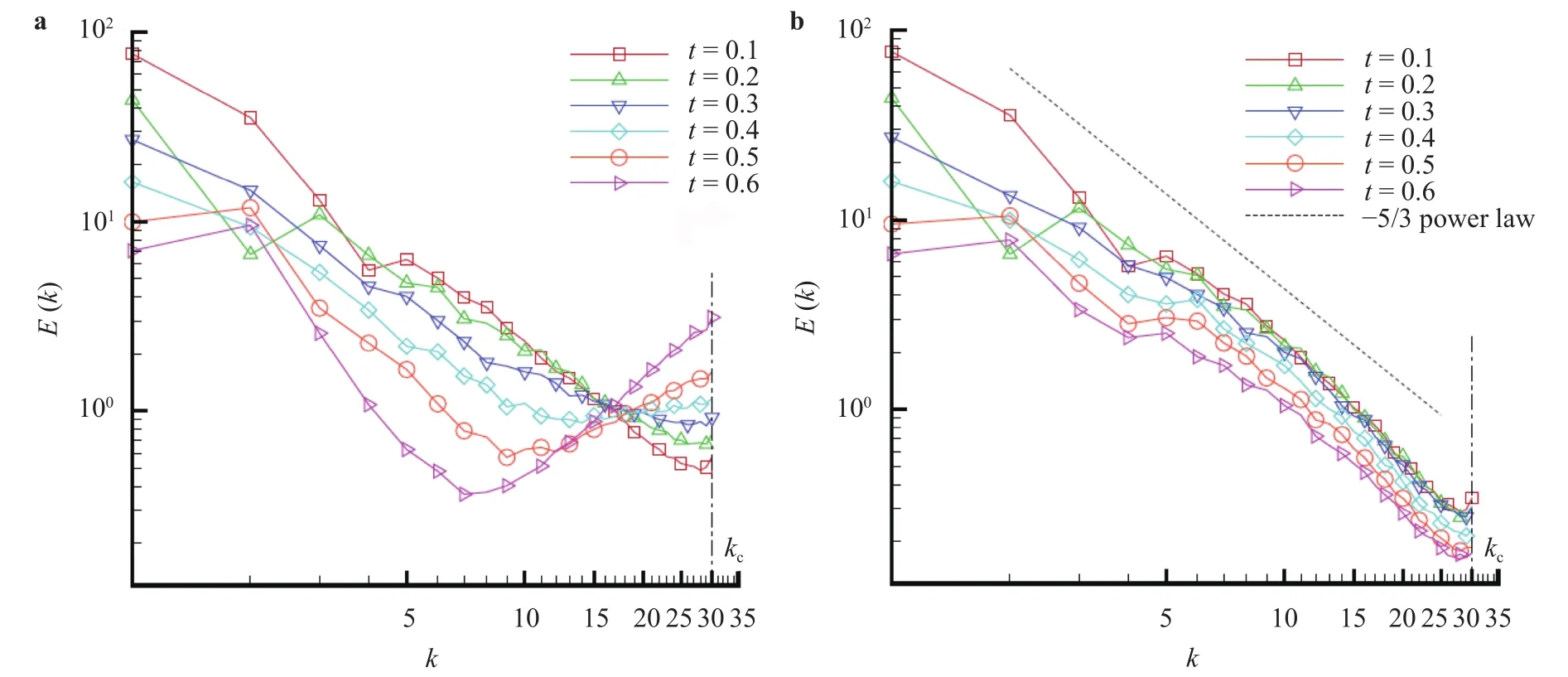
Fig. 1. Time evolution of energy spectra in a free-decaying turbulence 643 grids [13]. a CZZS model with dynamically determined model coefficient; b CZZS model with fixed resolved-scale scaling law.
Two important extensions of the CZZS model can be the studies made by Shao et al. [22] and Cui et al. [23]. The former extension involves homogeneous rotation, while the latter one considers homogeneous shear instead. The eddy-viscosity assumption remains in these models as the basic assumption.Similar extensions can also be found in Ref. [24] for determining the Smagorinsky coefficient, and in Ref. [25] based on the eddydiffusivity assumption for passive scalar. Another extension of the CZZS model uses the velocity increment assumption to replace the eddy-viscosity assumption and obtains an improved velocity increment (IVI) model [11], which has an very simple model formulation and reduces the calculation resources in practice.
We remark that although the theoretical background of these rational SGS models is solid, presently there are still no practical applications of these models in real engineering problems. Except for the lack of propagation, we have to admit that sometimes these models are not numerically stable enough. We explained in Ref. [26] that this is partly because of the time-reversibility of KEF, which generates less SGS dissipation in non-equilibrium turbulence [27] but captures correctly the short-time evolution physics [28, 29]. However, this problem is indeed a methodological issue, which calls for the following high-level methodological investigations for the rational SGS modelling technique.
As discussed above, we found that when employing these SGS models, if we calculate the model coefficient dynamically,the LES calculations are usually unstable. Instead, a constant model coefficient usually leads to better performance. This fact has been discussed in Refs. [3, 11, 13], but we did not manage to give a convincing theoretical explanation. Based on the definition of the terms assumption and restriction, in Ref. [3] we summarized the various attempts of this modelling methodology,and phenomenally guessed that there are some conflicts among the assumptions and restrictions in SGS modelling. The following investigations then show preliminary attempts under this framework.
In Ref. [5] we find a typical criterion of orthogonality with one assumption and multiple restrictions of stationarity. We show by a generalized derivation that if there are multiple stationary restrictions in a modelling, the corresponding assumption function must satisfy a criterion of orthogonality. Numerical tests using one-dimensional nonlinear advection equation are performed to provide some validations on this approach. See Fig. 2 for illustration, in which we tested different cases with various combinations of restrictions. Clearly, when the orthogonal relations of these restrictions are not satisfied, errors are always nonnegligible. This case is indeed too ideal to be validated and employed in real SGS modelling, since no real SGS model uses only stationary restrictions, however, it explicitly shows the existence of mathematical constraints in the methodology of SGS modelling, which has never been clarified in previous studies.

Fig. 2. Error evolution of restrictions [5]. a Restriction h1; b restriction h2. The filled symbols correspond to orthogonal relations, the empty symbols otherwise.
Starting from these works, we also attempt to derive more general mathematical constraints for different restrictions. For example, by defining the restriction of multiscale law they can be obtained mathematically in more general formulations [6]. We therefore have much confidence on this methodological topic,and hope that this can be helpful in the future for guiding the rational SGS modelling practices.
Beside, there are also other attempts for methodologically investigating the SGS modelling problem. For example, Wang and Li [30] investigated the best ratio between filters for the scale similarity assumptions. We remark that these attempts show the tendency that researchers are now more interested at clarifying the methodologies of LES modelling, instead of deriving a new model formula.
In conclusion, in this contribution we review the various attempts of rational SGS modelling by employing the KEF. Aiming at explaining and solving the underlying problems, we also introduce the previous methodological investigations for the rational SGS modelling technique, which are expected to provide instructive criterions for not only the rational SGS modelling, but also other types of SGS modelling practices.
Despite the advantages of the rational models as described in this contribution, the constraints also exist which prevent the rational models from being widely employed. The first constraint is the low model dissipation which sometimes cannot guarantee numerical stability. This is indeed a natural result, since in rational models we always start from the Navier-Stokes equations and the SGS term is written in a non-linear form by definition.We expect the SGS term to dissipate energy, but formally the non-linear form is always time-reversible (which means that changing all velocitytodoes not change the signal of the non-linear form) but the dissipation term is always time-nonreversible [26, 27, 31]. This fact touches the philosophy of turbulence: some phenomenological SGS modellings artificially“break the time-reversibility” [32], but the rational methodology does not permit this artificial treatment. Involving an additional equation for the third-order moment might be a rational solution and will be considered in our future work. Another constraint of the rational models is the unclear question of the starting point of non-linear multi-scale modellings: all information of rational models are derived from the Navier-Stokes equations,but if we do not involve external restrictions, are the Navier-Stokes equations enough to generate information to close themselves? This is indeed a fundamental mathematics question on non-linear science, while we expect that the future advance of non-linear science will help clarify this confusion.
Acknowledgement
We are grateful to Liang Shao, Jean-Pierre Bertoglio, Zhao-Shun Zhang, Gui-Xiang Cui, Zi-Xuan Yang, Wouter Bos, and Guo-Wei He for the many useful discussions on the related topics. This work is supported by the National Natural Science Foundation of China (11772032, 11572025, and 51420105008).
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Rowing jellyfish contract to maintain neutral buoyancy
- Effects of tide-surge interaction and wave set-up/set-down on surge: case studies of tropical cyclones landing China's Zhe-Min coast
- Wave reflection in semiconductor nanostructures
- Achieving thermal magnification by using effective thermal conductivity
- Numerical investigation on convective heat transfer over two heated wall-mounted cubes in tandem and staggered arrangement
- Nonlinear thermo-structural behavior of sandwich panels with truss cores under through-thickness gradient temperature field
