Wave reflection in semiconductor nanostructures
2018-07-27FeixiangTangYaqinSong
Feixiang Tang, Yaqin Song*
State Key Laboratory for Strength and Vibration of Mechanical Structures, School of Aerospace, Xi’an Jiaotong University, Xi’an 710049,China
Keywords:
ABSTRACT Based on nonlocal thermoelastic theory, this article studies the reflection of waves in nanometer semi-conductor media. Firstly, the governing equations are established based on coupled nonlocal elasticity theory, plasma diffusion equation, and moving equation. Then, using the harmonic method, the solution of the dissipation equation and the analytic expression of the reflection coefficient rate are obtained. Finally, the influences of nonlocal parameters on wave velocities are showed graphically. It is found that after the introduction of nonlocal effect, the phase and group velocities all show the attenuation, and as the frequency increases, the nonlocal parameter is bigger, and the decay rate is faster. The reflection coefficient rate varies greatly with different theories, with different reflection coefficient rates depending on the incident angle.
Micro- and nano-structures have been used widely in many fields like biological, medical, environmental, etc. With the reduction of size, the study showed that the state of the object is not only related to the state of the current point, but also related to other matter points and historical time. Nonlocal theory can be used to describe this characterization. There are many nonlocal theories, such as stress gradient theory [1], strain gradient theory [2], and so on. Compared with classical elasticity theory,the results from nonlocal elasticity theory showed better agreement with molecular dynamics simulation [3] and phonon dispersion test observations.
Classical Fourier heat conduction law [4, 5] can explain the relationship between the heat flux density and the temperature gradient. However its defection is that the temperature control equation is a parabolic partial differential equation, indicating that the thermal signal spreads at an infinite rate, which is inconsistent with the hysical reality in low temperatures or very short heat conditions. In order to correct this defection, generalized thermoelastic theories were born. Lord–Shulman (LS) theory [6] and Green–Lindsay (GL) theory [7] have been widely used. The LS model and GL model introduces one or two thermal relaxation times, which allows the thermal signal to propagate at a finite velocity, and the two theories are in different structures. One cannot exist as a special case of the other’s,but both can be degenerated to the traditional classical dynamic(CD) theory, which represents the classical thermoelastic theory based on Fourier's law). CD theory is sufficient for a large number of practical engineering problems, but the LS and GL theories can be more accurately solved when the thermal effects are extremely short or at very low temperatures, such as laser pulse heating.
With the decrease of dimension for nanostructure, the wave properties will have significant difference compare to macro-structure. The wave frequencies will reach to TeraHertz. This kind of wave will carry enormous energy. So it is of great significance to study the propagation and reflection behavior of nanostructures. Based on the stress gradient nonlocal elasticity theory, the wave characterization and reflection problem of wave in semiconductor nanostructures is studied in this article.
In the process of analyzing the propagation of waves in the semiconductor medium, it is necessary to consider the coupled heat wave, elastic wave and plasma diffusion. Using the stress gradient nonlocal theory, the physical quantityis introduced, in whichis the material constant characterizes the nonlocal effect,is the material characteristic length. The semiconducting medium is assumed as a homogeneous isotropic material, the control Eqs. (11)-(13) are:
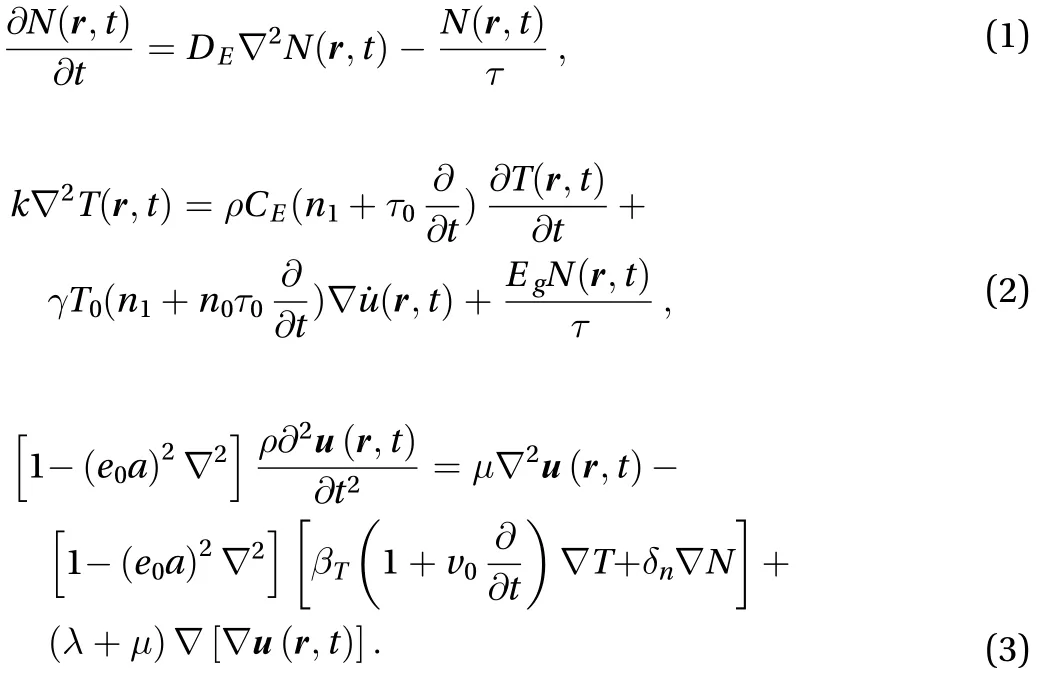
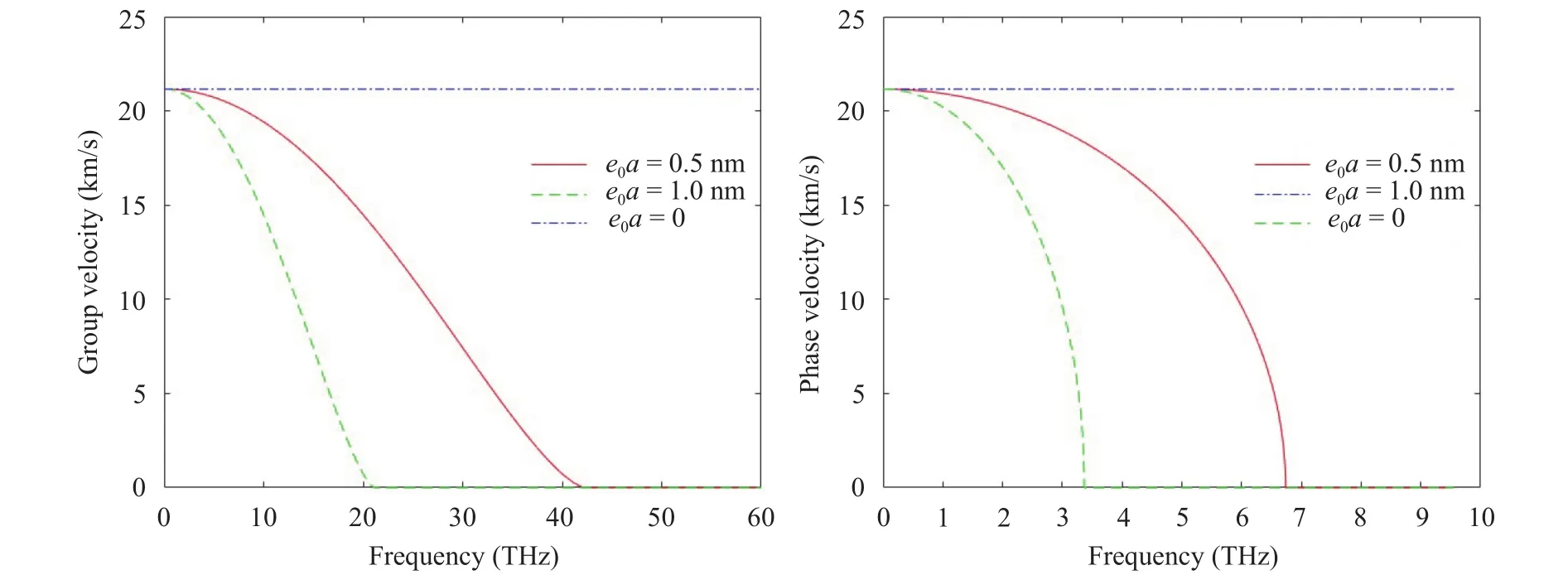
Fig. 1. Group velocity, phase velocity-frequency diagram.
When the parameter takes a specific value, it represents a different theory:
The displacement potential functionsandare introduced and defined as:
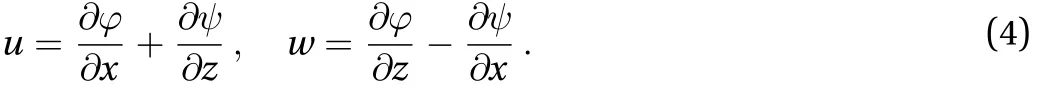
For ease of handling, introduce the following dimensionless quantities:
Consider the propagation of the wave in the x–z plane. Assuming the incident angleis the angle between the x-axis and the z-axis, we can set the solution as follows:
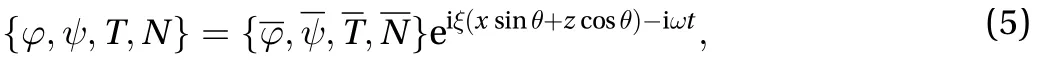
Substituting Eqs. (5) into non-dimensional Eqs. (1)-(3), we obtain four homogeneous equations:
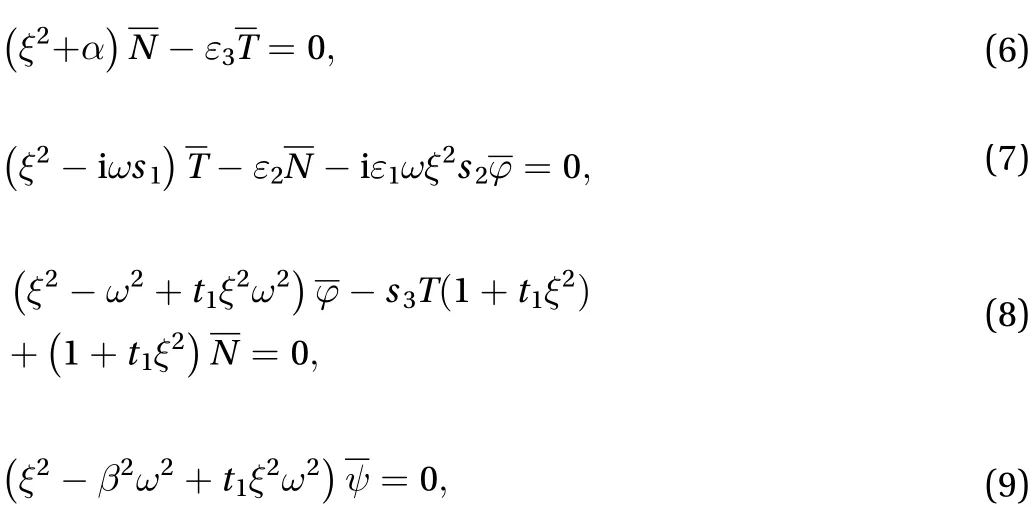
in which
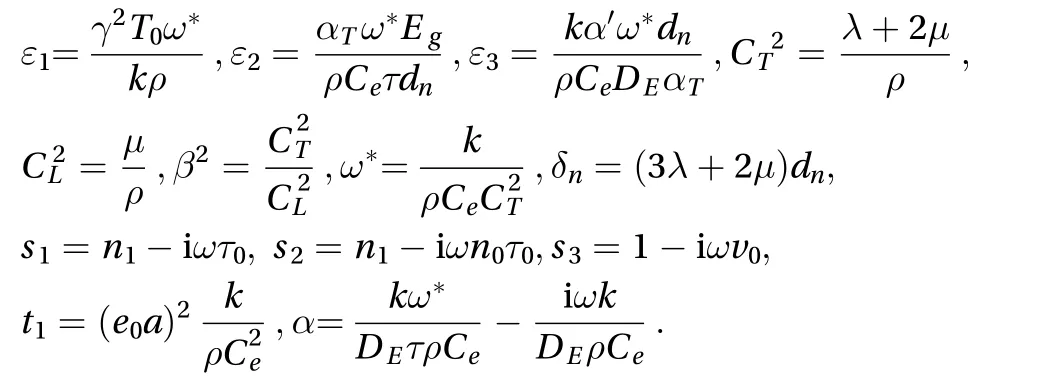
To obtain nontrivial solution for field quantities, the determination of coefficient matrix must satisfy:
From the definition of phase velocity and group velocity, we know that the phase speed and group speed are :
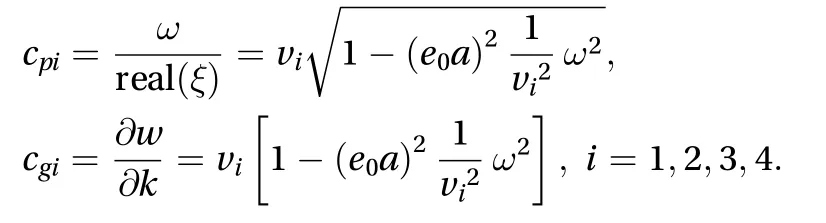
When the nonlocal parameter is 0, the wave velocity can be reduced to the result of classical theory.
Suppose the potential functionis as follows:
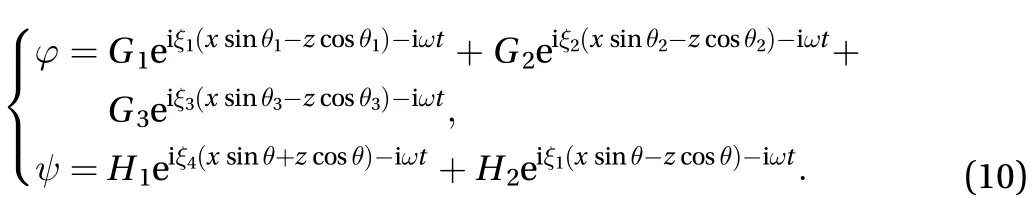
Boundary conditions can be given below:
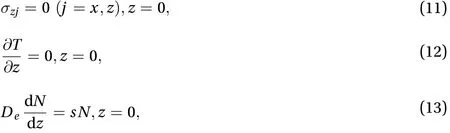
Substituting Eq. (10) into boundary conditions, the reflection coefficient ratiocan be obtained from:

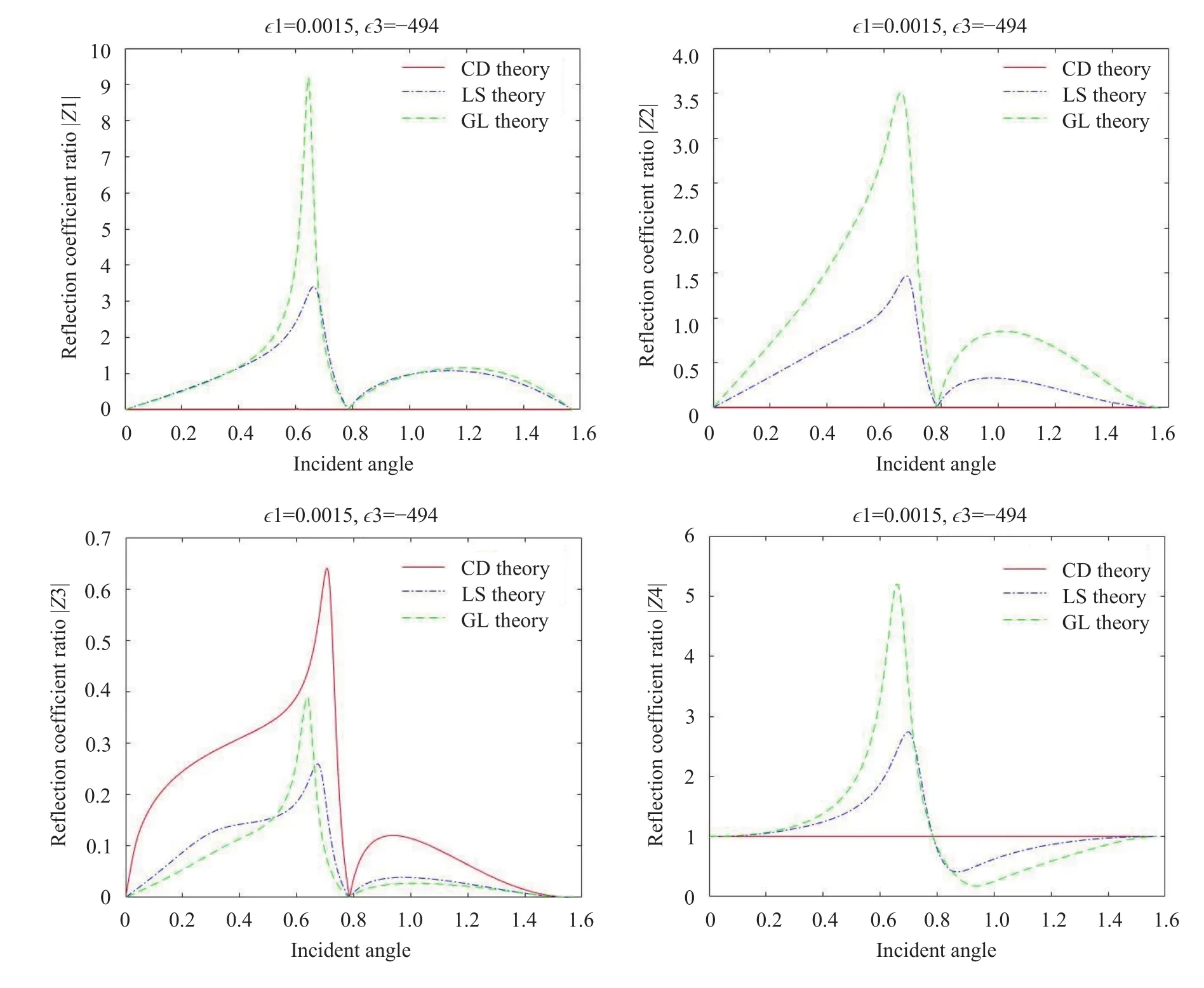
Fig. 2. Consider the local effect of three different theories under the reflection coefficient rate.
Selecting the semiconductor material silicon for numerical calculation, the material constant is as follows:
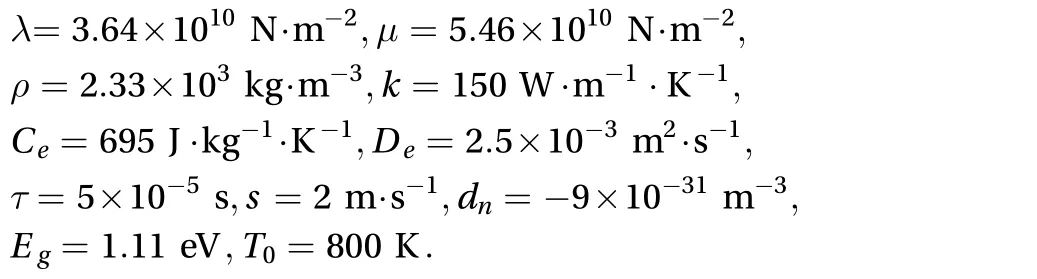
The heat relaxation time is usually different for different materal. For metel material is between 1 ×s and 1 ×s.For semiconductor materials, this article takes:
Figure 1 shows the changed relation between the group velocityand the phase velocitywith different frequencies,and the non-local parameters:the group velocity and the phase velocity in the classical local theory, that is, the wave does not change its shape in the propagation, which is because of the linear relationship between the wave number and frequency under the nonlocal theory. It can be observed that the velocity and phase velocity of local and nonlocal theoretical theories are equal when the frequency is zero. In the nonlocal theory, the group velocity decreases with increasing frequency. When the frequency is greater than a certain frequency (escape frequency), the group velocity becomes 0. It is because the wave number tends to infinity out of this frequency, and the wave has local and static characteristics.
Figure 2 gives the reflection coefficient ratio under different thermos-elastic theories (CD, LS, and GL) for incident rotational wave when non-local parameters. It can be seen that the reflectivity coefficient varies with the angle of incidence.Under CD theory and generalized theory (LS and GL), the reflection coefficient is very different. The reflection coefficient rate is|Z4| = 1 and the rest of the reflection coefficient is zero when the incident angle takes.
In this paper, the propagation characteristics of the wave in the nanostructured semiconductor structure under the nonlocal generalized thermos-elasticity theory are studied. The results showed that the phase velocity and the group velocity have the trend of recession, and with the increase of frequency, the higher the non-local parameters, the faster the decay rate. Also there is a significant difference between the reflection coefficients under different theories (CD, LS, and GL), and the reflection coefficient is different with the difference of incident angle. The frequency of propagating wave in nanostructures will reach up to TeraHertz, the conventional thermoelastic theory (CD theory)will not suitable to describe the behavior of structure. So generalized LS and GL theory will be better to explain the thermoelastic effect of nanostructure.
Acknowledgements
The work was supported by the National Natural Science Foundation of China (11672224).
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Rational subgrid-scale modelling: a short survey
- Rowing jellyfish contract to maintain neutral buoyancy
- Effects of tide-surge interaction and wave set-up/set-down on surge: case studies of tropical cyclones landing China's Zhe-Min coast
- Achieving thermal magnification by using effective thermal conductivity
- Numerical investigation on convective heat transfer over two heated wall-mounted cubes in tandem and staggered arrangement
- Nonlinear thermo-structural behavior of sandwich panels with truss cores under through-thickness gradient temperature field
