Rowing jellyfish contract to maintain neutral buoyancy
2018-07-27PtriciYngMtthewLemonsDvidHu
Ptrici J. Yng, Mtthew Lemons, Dvid L. Hu,b,*
a Schools of Mechanical Engineering , Georgia Institute of Technology, Atlanta, GA 30332, USA
b Schools of Biology, Georgia Institute of Technology, Atlanta, GA 30332, USA
Keywords:
ABSTRACT Jellyfish are easily carried by ocean currents, yet most studies on jellyfish focus on the kinematics in a quiescent fluid. In this experimental and theoretical study, we focus on rowing jellyfish, those that partially contract their bells and paddle in a relaxed manner. We film six species of rowing jellyfish in a range of background flow speeds at the Georgia Aquarium. Each species has a unique contraction frequency, which is independent of both the body orientation and the background flow speed. Our mathematical model reveals that jellyfish contract to offset their sinking. This behavior is invariant: Despite the background flow conditions, jellyfish contract as if they are oriented upright in a quiescent fluid. Our study suggests that jellyfish operate in open-loop without feedback from their environment.
Ocean currents vary in speed from regular currents of 0.08 m/s to a storm of 2.5 m/s [1, 2], which affect a number of aquatic organisms. Jellyfish are particularly susceptible because they swim relatively slowly by contracting and relaxing their bellshaped bodies. The magnitude of jellyfish contraction is associated with two propulsive modes: jetting and rowing. A jetting jellyfish fully contracts its bell, yet a rowing jellyfish only partially contracts its bell and paddle in a more relaxed manner [3].In 1983, Daniel proposed that the bell contraction is the source of thrust for jetting jellyfish [4, 5]. Later studies accept this concept and further state that jetting jellyfish contract at the natural frequency of the bell, which reduces the energy cost of swimming [6-8] and maximize propulsive efficiency [9]. Besides jetting jellyfish, rowing jellyfish have been investigated by visualizing the full cycle of contraction [10-13]. However, these studies have been focused on jellyfish in a quiescent fluid. The goal of this study is to determine how background flow influences the kinematics of jellyfish.
Early theoretical studies have classified the forces on jellyfish as thrust, drag, added mass force, and inertia force [4]. The four forces provide a theoretical framework in later jellyfish studies[9, 14], which neglect buoyancy force for simplicity. In 1981,Mills observed that most jellyfish sink in water. Jellyfish maintain themselves at a preferred depth by assuming a characteristic swimming pattern [15].
In this study, we incorporate the jellyfish sinking into a mathematical model and discuss its contribution to the kinematics of jellyfish. We first report the morphology of jellyfish and its kinematics in background flow. We then present the mathematical model for jellyfish swimming and compare its prediction to our observations. We lastly discuss the implications of our work and suggest directions for future research.
We model the shape of jellyfish as a section of a hemi-ellipsoid with densitydiameter D, height H, and mass mjas illustrated in Fig. 2(a). Previous researchers have observed that most jellyfish are negatively buoyant [15, 16]. However, none have measured the density directly because measuring the volume of the soft and fragile jellyfish is challenging. Gemmell assumes that density of jellyfish Aurelia aurita is

and examine the sinking of static jellyfish in a numerical model[12]. Since the density of seawater is 1.020 g/cm3, jellyfish A.aurita are 0.5% denser than water [12]. For simplicity, we assume that all jellyfish species have the same density.
In 2007, Dabiri compiled the morphology of 660 jellyfish spe-cies [11]. Using Dabiri's and our data, the relationship between jellyfish bell height H and diameter D may be written
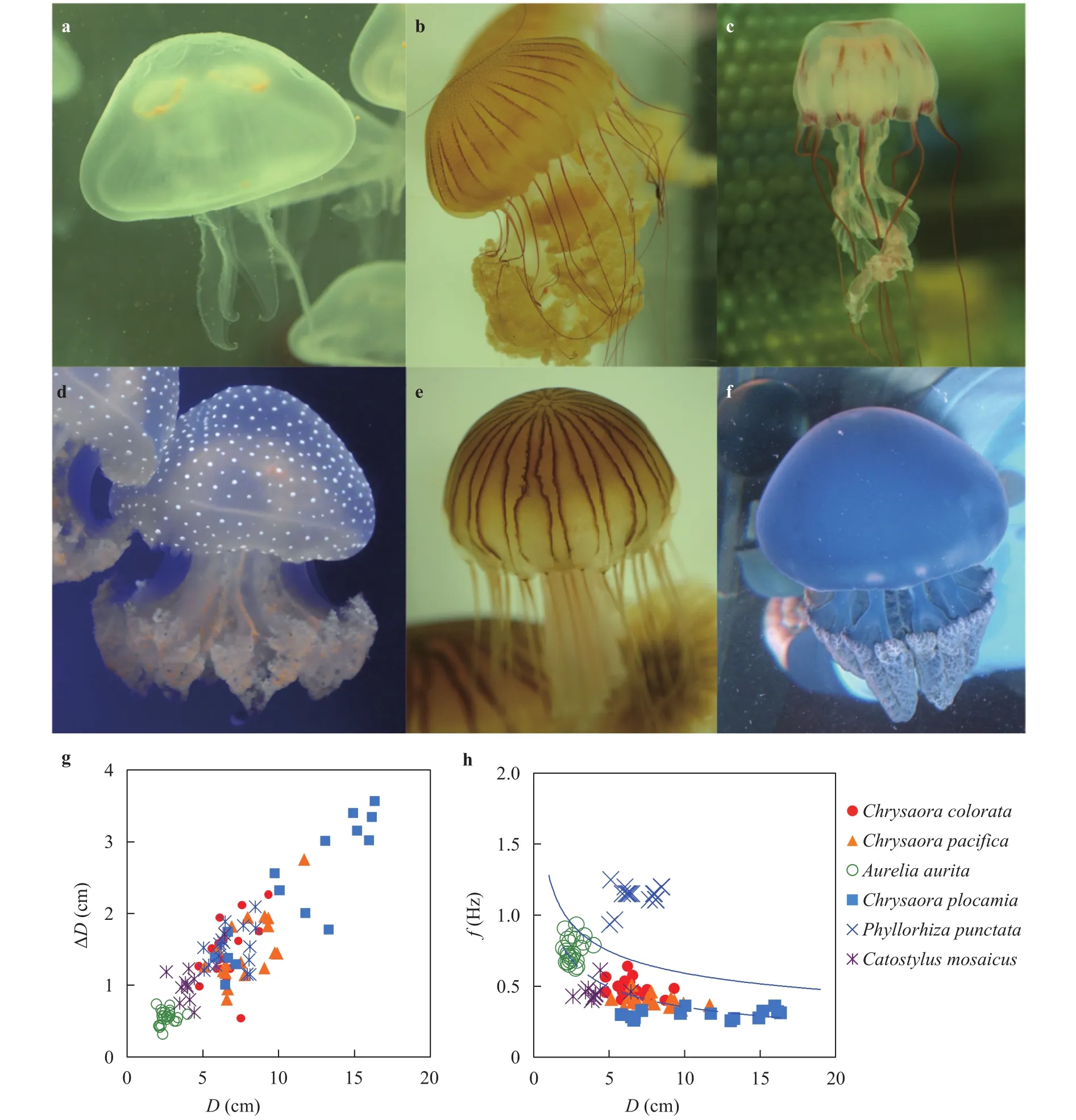
Fig. 1. a Aurelia aurita. b Chrysaora plocamia. c Chrysaora colorata. d Phyllorhiza punctata. Courtesy of Marco Fumasoni in Wikimedia Commons. e Chrysaora pacifica. f Catostylus mosaicus. Courtesy of Steven Johnson in Wikimedia Commons. g-h The relationship between the diameter of jellyfish D and g the contraction amplitude , h the contraction frequency f. Symbols represent experimental measurements, the dashed line represents best fit to the data, and the solid line represents the theoretical prediction.
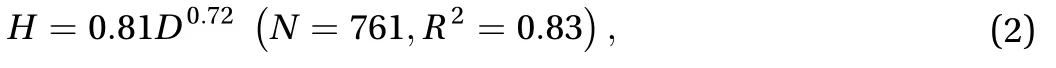
where H and D are both in cm. The height of the bell increases disproportionally with body size as shown in Fig. 2(d).Consequently, small jellyfish are prolate (bullet-shaped), while large jellyfish are oblate (plate-shaped), as reported in previous studies [3, 17].
The wet mass of jellyfish mjis complied from previous literature [18-20]. Its relationship to diameter D may be written
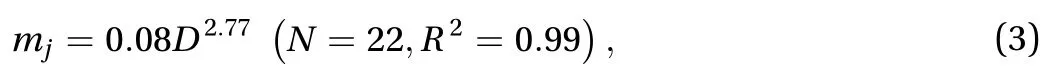
where D is in cm and mjis in grams. This trend indicates that the mass increases disproportionally with body size as shown in Fig.2(e). Larger jellyfish are lighter than expected from isometry(mj~D3). To understand the impact of morphology on the swimming kinematics, we turn to the filming of jellyfish.
We film six species of jellyfish at the Georgia Aquarium, including Aurelia aurita, Chrysaora plocamia, Chrysaora colorata,Chrysaora pacifica of the Order Semaeostomeae and Phyllorhiza punctata and Catostylus mosaicus of the Order Rhizostomeae(Fig. 1(a) to (f)). The jellyfish are of a broad range of size from 2 to 20 cm, which are identified as rowing jellyfish in previous literature [3]. The jellyfish are held in aquaria with constantly circulating background flow as illustrated in Fig. 2(c). The aquarium staff do not permit us to turn off the flow off and state that all species sink to the bottom of the tanks except C. mosaicus. This anecdotal sinking for five of the six species is qualitatively consistent with our assumption that jellyfish have a greater density than water. We measure the flow speed by tracing particles next to the jellyfish but not near the jet from the bell. For each species, we adjust the background flow speed in the range of 1 to 8 cm/s. Overall, we conduct 24 experiments of jellyfish swimming in different flow conditions.
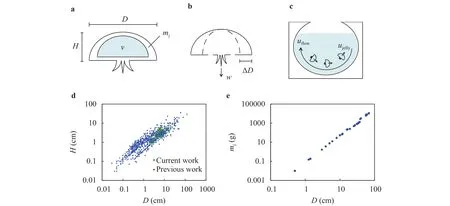
Fig. 2. a-b Schematic of a The dimensions of jellyfish and the trapped water. b The contraction of jellyfish. c The circulating water in the jellyfish tank of speed uflow, and the jellyfish successfully swimming upstream with speed ujelly. d The relationship between the diameter of jellyfish D and the height of jellyfish H. e The relationship between the diameter of jellyfish D and the wet mass of jellyfish mj.
Jellyfish are carried by background flow in most experiments.The velocity of background flow is labeled as uflowand the velocity of jellyfish swimming is labeled as ujelly. Here we investigate only cases in which jellyfish swim parallel to background flow.There are three cases because jellyfish can be pushed by background flow in one of two orientations. In addition, the jellyfish can successfully swim upstream.
When jellyfish swim with the current, they are pushed by the flow as shown in Fig. 3(a). Half of the species, including P.punctata, C. plocamia, and C. mosaicus, have swimming speeds equal to the current speed. When jellyfish are pushed by the current in the inverted orientation, they reach a range of speeds (0 to 6 cm/s), as shown in Fig. 3(b). Jellyfish in both orientations are pushed by background flow. Conversely, if the jellyfish swim against the current, the speed of jellyfish is limited to less than 2 cm/s as in Fig. 3(c). The strength of the jellyfish is insufficient to swim strongly against the current.
We quantify the bell contraction of jellyfish by amplitudeand frequency f. The product of amplitude and frequency,indicates the speed of the bell contraction. Among the six species, only P. punctata has an abnormally high product of amplitude and frequency, which ranges from 1 to 2.5 cm/s. The remaining species have slow bell speeds of less than 1 cm/s as shown in Fig. 3(d). Since bell speeds are less than speeds of background flow (1 to 8 cm/s), it explains that our jellyfish are futile swimmers.
The bell contraction is a function of body size, which is independent of jellyfish swimming and background flow. Figure 4 shows amplitude and frequency of the bell contraction across jellyfish swimming speeds and background flow speeds. The contraction amplitude is constant for only one species A. aurita,= 0.55 ± 0.10 cm (), while that of the remaining five species has no clear relation with the speeds of either jellyfish swimming and background flow, as in Fig. 4(a)-(b). Instead, the amplitude of contraction is a function of body size. The scaling of contraction amplitude is proportional to the diameter of bell,
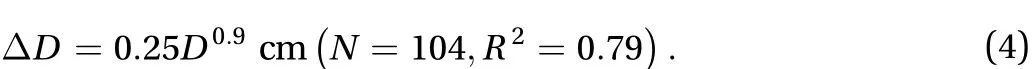
Jellyfish contract their bell with the amplitude of 25% of their diameter as in Fig. 1(g).
The frequency of contraction is much more consistent than the amplitude. Specifically, the frequency is a separate constant for each species, as shown in Fig. 4(c)-(d). The frequencies are also remarkably consistent, and they have a standard deviation around 10 percent of the average: 0.49 ± 0.06 Hz) for C.colorata, 0.40 ± 0.04 Hz) for C. pacifica, 0.75 ± 0.09 Hz() for A. aurita, 0.30±0.03 Hz () for P. punctata,and 0.45±0.06 Hz () for C. mosaicus. It is noteworthy that the frequency is maintained independent of the direction of background flow.
The frequency of contraction is also a function of the body size. The scaling of frequency is inversely proportional to the diameter of bell as shown in Fig. 1(h),
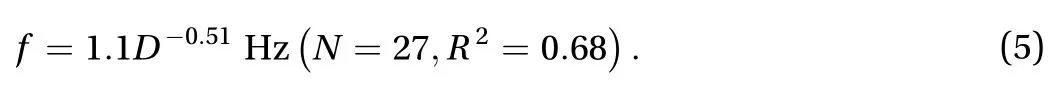
The frequency is similar to McHenry's previous scaling on one species A. aurita ranging in the diameter from 1.6 to 9.5 cm: f =25D-0.88Hz (N = 25, R2= 0.83) [10]. Our exponent indicates a similar trend but the pre-factor is 25 times less. The inconsistency might be due to the selection of species, since we have six species and each of them is of a relatively small range of size. We now turn to a mathematical model of jellyfish swimming and show that our prediction of the frequency is more consistent with Eq. (5).
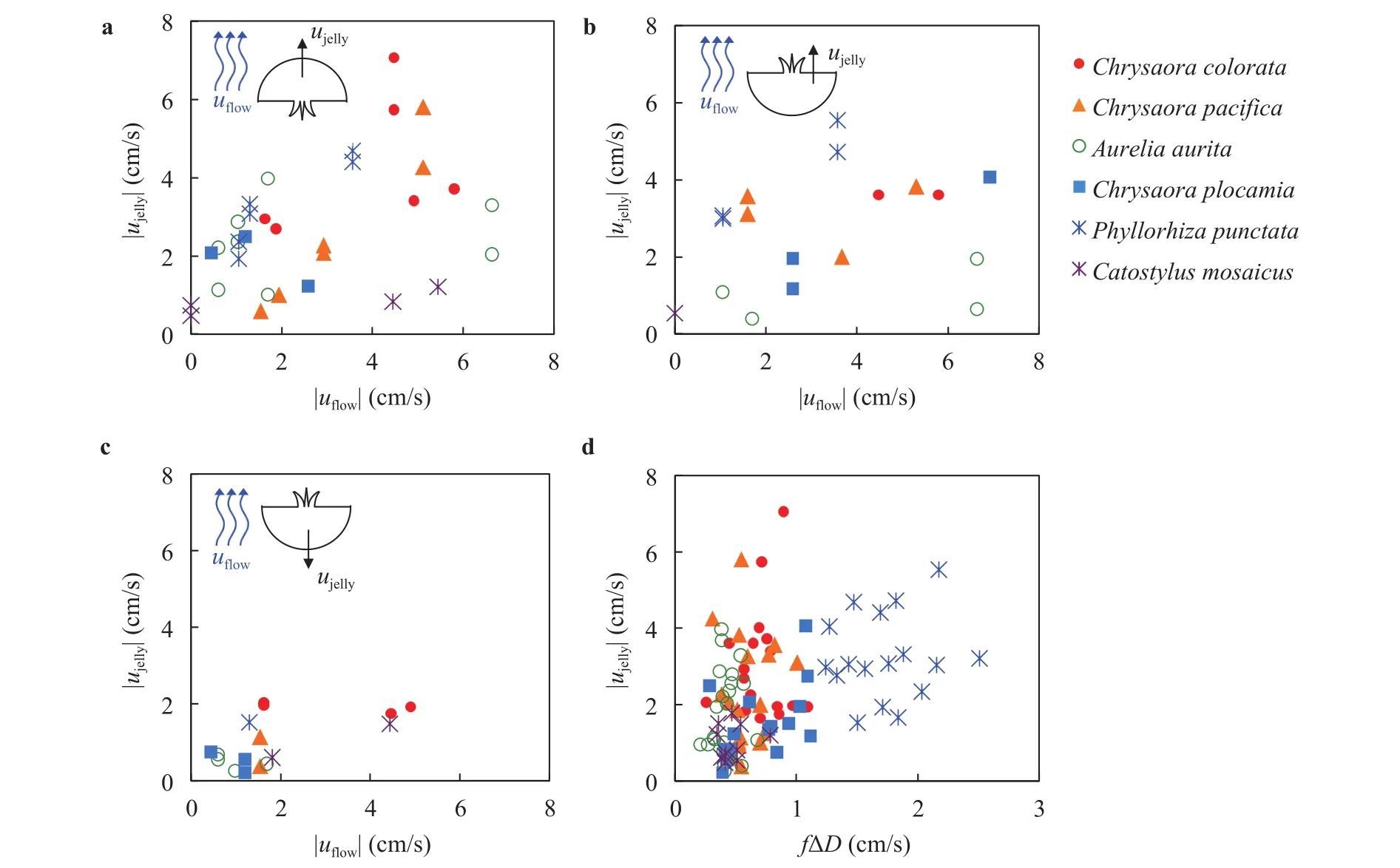
Fig. 3. a-c The relationship between the speed of background flow |uflow| and the speed of jellyfish |ujelly| in three categories. a Jellyfish pushed by the current. b Jellyfish unsuccessfully swim against the current. c Jellyfish successfully swim against the current. d The relationship between the product of contraction frequency and amplitude and the speed of jellyfish |ujelly|.
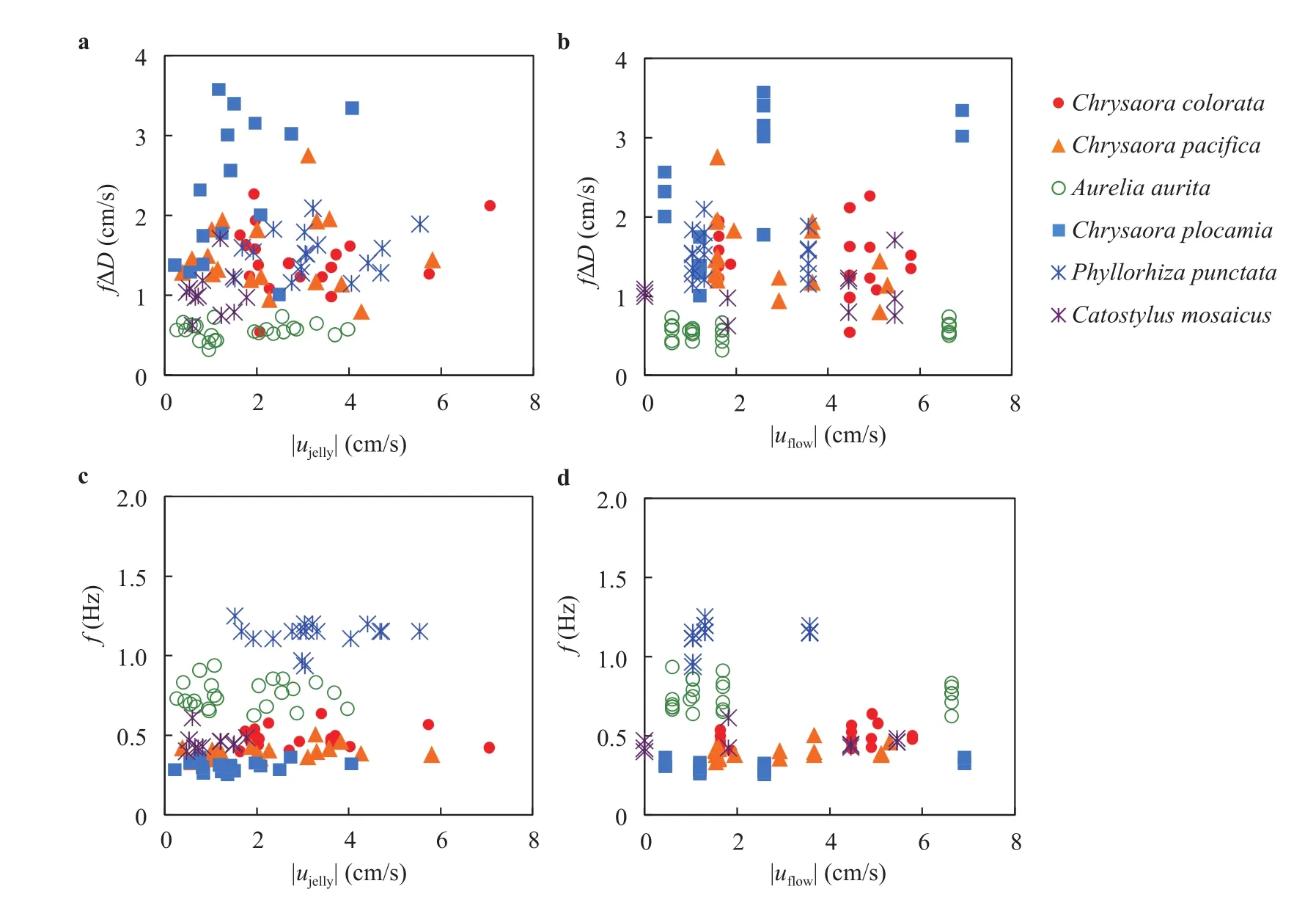
Fig. 4. a-b The relationship between the contraction amplitude and a the speed of jellyfish |ujelly| b the speed of background flow |uflow|. cd The relationship between the contraction frequency f and c the speed of jellyfish |ujelly| d the speed of background flow |uflow|.
We present a hydrodynamic model for jellyfish swimming steadily at velocity ujellyunder background flow at flow velocity uflow. Since jellyfish undergo periodic contractions, their swimming is unsteady on the time scale of a single period. Nevertheless, here we focus on an average swimming speed across multiple cycles, a state we consider as steady. Moreover, we only discuss the cases of jellyfish swimming with or against the current.Therefore, our model is steady-state one-dimensional.
When jellyfish swim, the forces on jellyfish are composed of their inertia, the added mass force, thrust by jet creation from contraction, drag, and buoyancy,

The inertia force is the product of jellyfish mass and the acceleration of swimming, Finertia=Vjdujelly/dt, whereis the density of jellyfish and Vjis the volume of jellyfish. The added mass force is the time rate change of water contained in the bell,Fadd-mass=dujelly/dt, whereis the density of water and V is the volume of the bell. We include the drag and thrust forces from Daniel [4, 5]. The drag force is Fdrag=(ujelly-uflow)2A/2,where Cdis the drag coefficient and A is the cross sectional area.The thrust force is Fthrust=|w, where w is the velocity of the jet relatively to the bell andis the change of cross-sectional area of the bell. The speed of the jet is the ratio of volumetric flowrate and the change of cross-sectional area, |w| = fV/,where f is the frequency of contraction. Previous models neglect the buoyancy force. The weight of jellyfish is. Bouyancy is the weight of the displacement water. The net buoyancy force is the Fbuoyancy= ()Vjg. In the case when jellyfish swim upwards, we rewrite Eq. (6) to obtain:
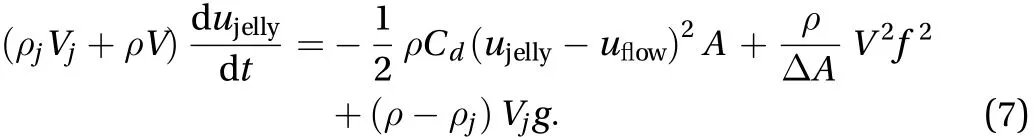
Equation (7) is one of the four cases since the orientations of both jellyfish and background flow may be upwards or downwards. It is impossible for jellyfish to contract at a single frequency and satisfy all four cases.
We propose a new and remarkably simple rule for jellyfish motion: Jellyfish contract to prevent sinking as if they are oriented upright in a quiescent fluid. Since the motion is steady state, we neglect accelerations. Moreover, the drag force is negibile because there is no fluid motion. Together, Eq. (7) simplifies to:

We rearrange rewrite Eq. (8) to express the frequency,
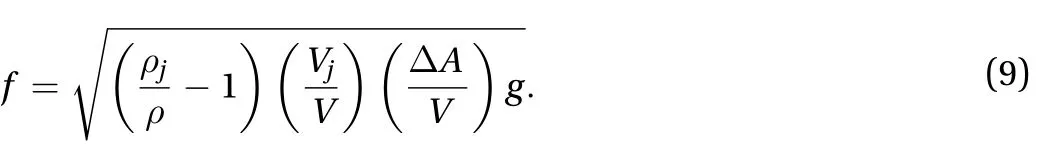
The allometry of jellyfish provides estimation of each term on the right hand side of Eq. (9). The volume of bell scales as V~HD2~D2.72. The change of cross-sectional area scales as~D~D1.9. For simplicity, we assume that the density of jellyfish,, is constant. Thus, the volume of jellyfish, which is the ratio of mass and density, scales as Vj= mj/~mj~D2.77.Substituting these expressions in Eq. (9) yields that the ratio of volumes is Vj/V~D0.05and area-volume ratio is/V~D-0.82.Thus, the area-volume ratio,/V, is the dominant term in Eq.(9). All together, the frequency of contraction is f~D-0.39. The exponent is of the same order as that in our experiments (f~D-0.51). We conclude larger jellyfish contract more slowly because of their lower area-volume ratios.
We go beyond scaling analysis to further simplify Eq. (9). We approximate the shape of jellyfish as a hemi-ellipsoid with height H and diameter D as shown in Fig. 2(a). The hemi- ellipsoid is composed of two parts: the volume of jellyfish and the volume of the bell. The volume of jellyfish is the ratio of mass and density, Vj= mj/The jellyfish is mainly composed by thin tissues, thus the volume of jellyfish body is much less than the encapsulation of the hemi-ellipsoid, VjV. The volume of the bell is approximated as that of the hemi-ellipsoid, V ≈ D2H/6.The change of cross-sectional area is≈Thus, the frequency of contraction is
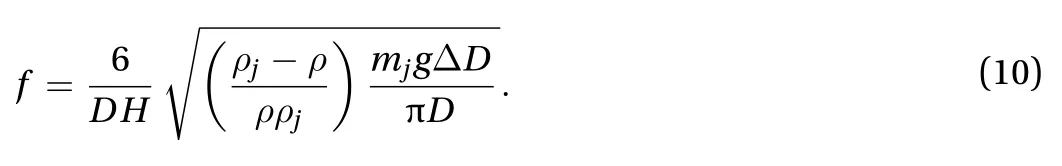
With the morphology of jellyifsh, Eq. (10) can be written f =1.3D-0.39, which corresponds to the solid line in Fig. 1(g). This line agrees well with our experiments, shown by the dashed line(f = 1.1D-0.51). Therefore, we conclude that our analysis captures the kinematics of jellyfish swimming.
The most surprising finding of our study is that jellyfish maintain constant frequency independent of their orientation under background flow. Since the drag force depends on orientation. Our result suggests that the drag force is too small to influence their frequency. A previous study has also shown that drag force is disproportionally less than other forces [10]. We derive the full governing equation for steady-state jellyfish motion, but do not attempt to solve it because a single contraction frequency cannot solve the equation in all flow directions. The influence of all involving forces has to be investigated case-by-case.
The scaling law presented in Eq. (5) is limited to rowing jellyfish. P. punctata has an anomalously high frequency for its body size. The species may satisfy a different scaling law, which might be further investigated by field experiments such as those by Katija [21], since these jellyfish are difficult to raise in captivity.Although we only have six species of rowing jellyfish from 2 to 20 cm, our mathematical model might be valid for more species.
We conduct an experimental and theoretical study of rowing jellyfish swimming under background flow at various speeds. We discover that each species has a unique contraction frequency,which is independent of both the speed of background flow and the orientation of jellyfish. We present a mathematical model of jellyfish oriented upright in a quiescent fluid. Their contraction frequency in these conditions matches well with observed frequencies, suggesting jellyfish do not change kinematics with their environment.
Below we present our experimental methods for filming and tracking jellyfish. The jellyfish are housed in the Jellyfish lab at the Georgia Aquarium in Atlanta. We use Sony HDR-XR200 to film jellyfish in the tanks present in the lab. Each tank has an adjustable flow which enters the tank through a bar with multiple exits over the width of the tank. We place the camera in line with the bar so that the camera is perpendicular to background flow.We film jellyfish with a known reference length on the surface of the tank. At each background flow setting, we obtain close up recording on jellyfish and zoom-out recording on background flow over the whole tank. The staff bring jellyfish to the surface of the tank and measure the diameter of them.
We use open-source software Tracker to analyze jellyfish over a full cycle of movement, which is defined as one full expansion of the bell to another. We track three points on the jellyfish at the full expansions and the full contractions: one on the top and two on the edge of the bell. These three points set the speed of jellyfish swimming, the contraction amplitude, and the contraction frequency. We split the direction of jellyfish swimming into four categories: with the current, with the current and inverted, against the current, and perpendicular to the current.
We visualize background flow by small particles (1 to 3 mm in diameter) in the tanks. The particles are zooplankton and dead skin cells from jellyfish. These particles are uniformly distributed in every tank. We use open-source software Tracker to measure the speed of a particle as that of background flow.
Acknowledgements
We acknowledge our funding sources Army Research Office 63207-EG, our photographer (S. Zan), and hosts at the Georgia Aquarium (L. Camp, M. Smith, K. Stone, and A. Arnold). We thank S. Kim and C. Apicella for their early contributions.
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Rational subgrid-scale modelling: a short survey
- Effects of tide-surge interaction and wave set-up/set-down on surge: case studies of tropical cyclones landing China's Zhe-Min coast
- Wave reflection in semiconductor nanostructures
- Achieving thermal magnification by using effective thermal conductivity
- Numerical investigation on convective heat transfer over two heated wall-mounted cubes in tandem and staggered arrangement
- Nonlinear thermo-structural behavior of sandwich panels with truss cores under through-thickness gradient temperature field
