A three-dimensional immersed boundary method for non-Newtonian fluids

Luoding Zhu*

Department of Mathematical Sciences and Center for Mathematical Biosciences, Indiana University - Purdue University, Indianapolis,IN 46202, USA

Keywords:

ABSTRACT Fluid-structure-interaction (FSI) phenomenon is common in science and engineering. The fluid involved in an FSI problem may be non-Newtonian such as blood. A popular framework for FSI problems is Peskin’s immersed boundary (IB) method. However, most of the IB formulations are based on Newtonian fluids. In this letter, we report an extension of the IB framework to FSI involving Oldroyd-B and FENE-P fluids in three dimensions using the lattice Boltzmann approach.The new method is tested on two FSI model problems. Numerical experiments show that the method is conditionally stable and convergent with the first order of accuracy.

Fluid-structure-interaction (FSI) problems are common in science and engineering. Because of the high level of complexity of such problems, analytical soultions are rare if not impossible.As an alternative to laboratory experiments, numerical solutions are viable. Among many numerical methods [1-9] developed for FSI problems, the immersed boundary (IB) method by Peskin[10] is probably the first framework for such problems.

Most existing versions of the IB method are formulated for Newtonian fluids. Note that the existing non-Newtonian versions [11, 12] are two dimensional. The existing three-dimensional (3D) version is formulated for power-law fluids [13].However, FSI problems are in general 3D and may involve non-Newtonian fluids necessitating more sophiscated constitutive models than power-law functions. Such FSI examples include cancer cell metastasizing through poroelastic tissues and cytoskeleton moving in cytoplasm. In this letter, we report an extension of our previous work [13] on power-law fluids to Oldroyd-B[14] and FENE-P [15] fluids in three dimensions. The constitutive equations are modelled by the FENE-P model (reducing to the Oldroyd-B model in an especial case) and numerically solved by the lattice Boltzmann D3Q7 model [16]. The fluid flow is modelled by the lattice Boltzmann equations and numerically solved by the D3Q19 model. The deformable structure and FSI are modelled by the immersed boundary method. As a test on the new method, we consider two FSI toy problems — a deformable plate being towed at its midline horizontally in an Oldroyd-B fluid and a flexible sheet being flapped at its leading edge vertically in an FENE-P fluid.

Consider a generic deformable structure moving in a viscous incompressible non-Newtonian fluid whose constitutive equations are modelled by the Oldroyd-B or FENE-P model. The immersed boundary formulation for such a problem in three dimensions may be written as follows. The motion of a non-Newtonian fluid may be governed the incompressible Navier–Stokes equations:

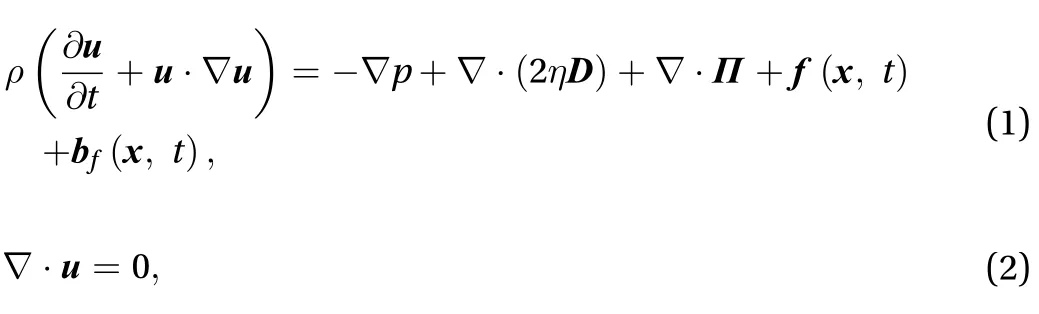
For non-Newtonian fluids such as polymeric fluid, the vis-coelastic stressmay be modeled by the FENE-P model [15]:where the polymer conformation tensor C is governed by

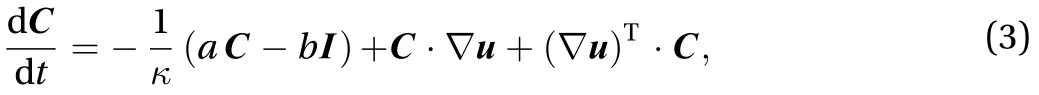
The Eulerian force density f in the Navier–Stokes equations is computed by

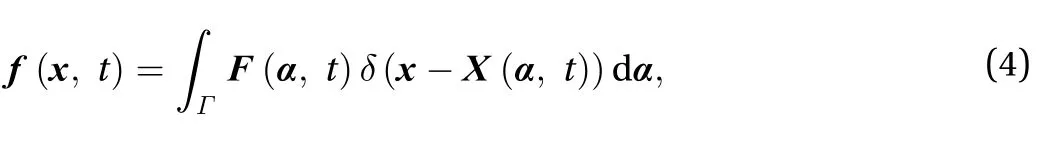
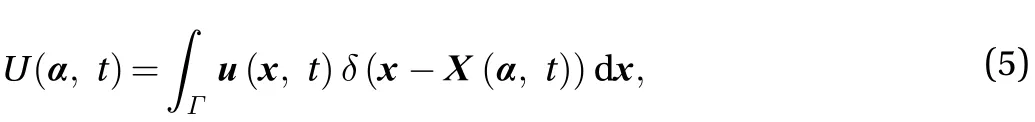
The 3D incompressible Navier–Stokes equations are solved using the lattice Boltzmann D3Q19 model [16, 17]. The particle velocity spaceis discretized by a set of 19 velocities. Let gj(x, t)be the distribution function along(j = 0, 1, ..., 18). The lattice Boltzmann equation (LBE) that advances gj(x, t) forward by one time-step is

where wjis the weightspeed of sound of the model, and c is the lattice speed associated to the D3Q19 model.The constants wjand c are model parameters. The external forceis treated by Guo’s approach [18]. The macroscopic variables such as densityand momentumcan be obtained from the gj(x, t) at each node. The functionis an expansion of the Maxwell–Boltzmann equilibrium distribution.

For viscoelastic fluids modelled by the Oldroyd-B or FENE-P models, the constitutive equations of the fluids [14, 15] are solved by a modified lattice Boltzmann model D3Q7 for advection-diffusion equations [19].

In a D3Q7 model, particles can move along six different directions of a node,, j = 1, 2, ..., 6, where= (−1, 0, 0),= (0,−1, 0),= (0, 0, −1),= (1, 0, 0),= (0, 1, 0),= (0, 0, 1).Particles may also be allowed to stay at the node= (0, 0, 0).Along each direction, j = 0, 1, 2, ..., 6 at a given node, the particle distribution function(corresponding to the component of the configuration tensor) is updated by

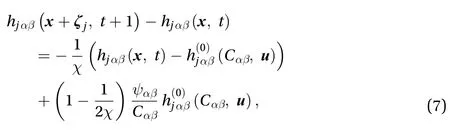
Two model FSI problems are considered: ① A deformable rectangular plate (initially placed vertically) is towed along its midline horizontally with a constant speed in a 3D rectangular box of an Oldroyd-B fluid. ② A flexible rectangular sheet (initially placed horizontally) is heaved up and down at one edge vertically and sinusoidally in a 3D rectangular box of an FENE-P fluid. In both cases, the fluid is initially still and driven to move by the motion of the structures. Periodic boundary condition is used on all of the three directions. The structures (plate and sheet) are modelled by two sets of uniform elastic fibers that are initially orthogonal to each other. There are three dimensionless parameters of the problems: flow Reynolds number Re, structure bending modulus, and fluid Weissenberg number Wi.Mesh refinement studies are performed for problem A. Many simulations with different combinations of the three parameters are conducted for both problems. Our numerical experiments indicate that the new IB method is convergent with first order of accuracy and is conditionally stable.

Some simulation results are given as below. In both cases,simulation results with the corresponding Newtonian fluid are also shown for comparison. The results with Newtonian fluids are obtained by setting Wi= 0 and keep all other parameters the same as in the non-Newtonian case.

The values of the dimensionless parameters are Re = 50,=0.0005, Wi= 0.1. The plate is placed intially on the y−z plane (i.e.vertically) in the middle of the box (in y and z directions) close to the left boundary. It is towed towards the right boundary along its midline with a constant speed. Figure 1 shows the position and shape of the plates at several time instantants. It is interesting to notice that the plate two free edges flap up and down in the Newtonian fluid and such flapping motion is not seen in the Oldroyd-B fluid.

The values of the dimensionless parameters are Re = 10,=0.005, Wi= 1. The sheet is placed intially on the x−y plane (i.e.horizontally) in the middle of the box along y and z directions with the left edge closer to the left boundary. Its right edge is heaved up and down sinusoidally (on the y−z plane along z-direction) in an FENE-P fluid. The z-coordiate of the leading edge isz (t) is the z-coordinate of the leading edge, A is the flapping amplitude, T is the period, and t is the time. The sheet is unconstrained otherwise and free to move in other directions. Figure 2 shows the position and shape of the sheets at several time instantants. It is interesting to notice that the right edge of the sheet in the Newtonian fluid has moved a distance towards the right boundary. But in the FENE-P fluid,the right edge of the sheet has stayed where it started and the sheet has not travelled any distance forward. The position and shape of the sheets show discernible differences some time after flapping starts. distance forward. The position and shape of the sheets show discernible differences some time after flapping starts.

Figure 3 demonstrates streamlines (surrounding the sheet)seeded from the same locations at the same time instant (1 × 105LB units, LB means Lattice Boltzmann). The top panel is the Newtonian case and the bottom one is the FENE-P case. It is seen that the fluid motion caused by the flapping sheet is more intense in the Newtonian case.

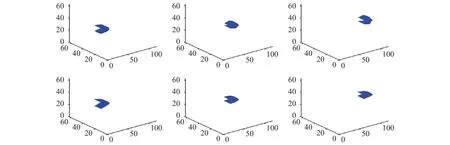
Fig. 1. Motions of the plate at different time instants in a Newtonian (top panels) and Oldroyd-B (bottom panels) fluid. The dimensionless parameters are: Re = 50, = 0.0005, Wi = 0.1. The time instants are 9484, 22700, 40580 in LB unit, from left to right, respectively. All parameters for the two cases are the same except the fluid property. The plate free edges perform up and down flapping motion in Newtonian fluid. The flapping motion is not seen in the Oldroyd-B fluid.

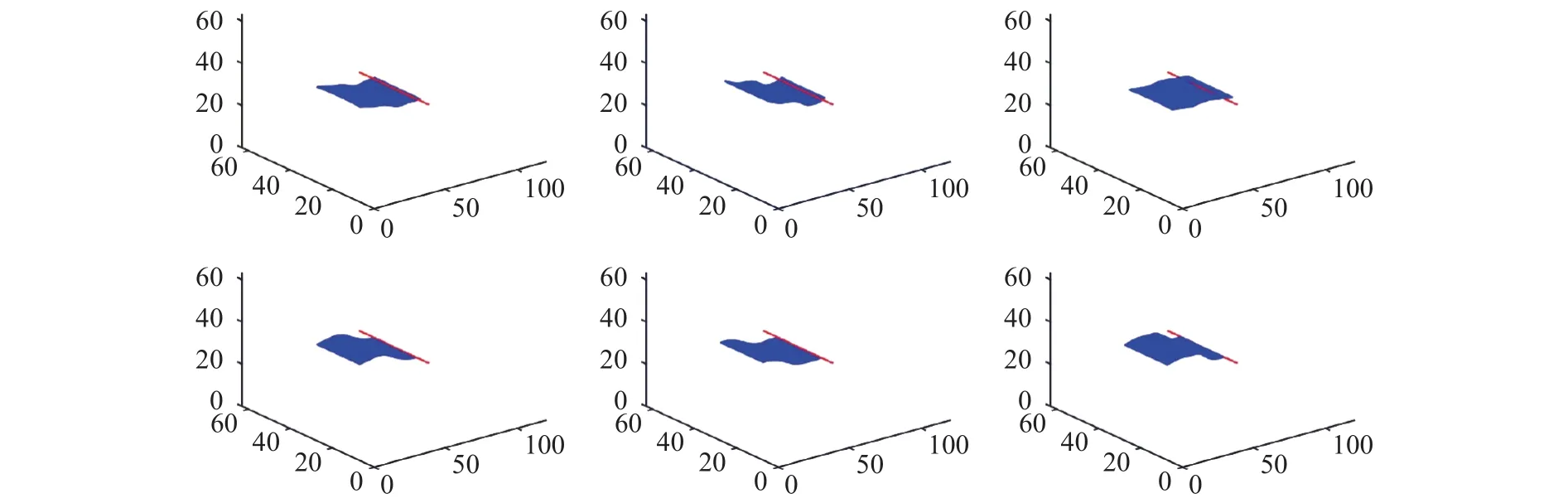
Fig. 2. Motions of the plate at different time instants in a Newtonian (top panels) and non-Newtonian obeying FENE-P model (bottom panels)fluid. The dimensionless parameters are: Re = 10, = 0.005, Wi = 1.0. The time instants are 4 × 104, 8 × 104, 1 × 105 in LB unit, from left to right,respectively. All parameters for the two cases are the same except the fluid property. The red line segment denotes the initial position of the sheet leading edge being flapped. As seen from the last column, the plate in a Newtonian fluid moves a distance forward along x-direction while the sheet in FENE-P fluid stays almost at its initial position.

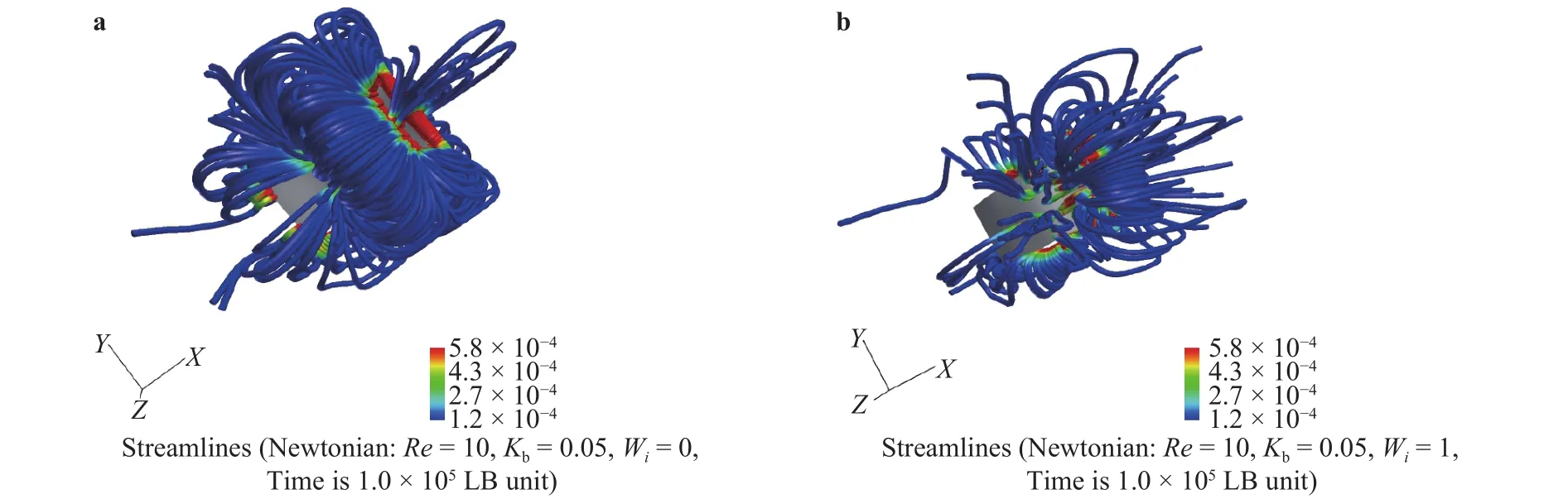
Fig. 3. Streamlines passing the same locations at the same instants around the sheet. a Newtonian fluid, b FENE-P fluid.

Our simulation results in both cases seem to indicate that the non-Newtonian fluids (Oldroyd-B and FENE-P) tend to suppress the motion of fluid. This may be caused by the presence of elastic force in the non-Newtonian fluid. Note that our result agrees with existing works [20].

We have developed a new IB method for non-Newtonian fluid-structure interaction in three dimensions. The lattice Blotzmann D3Q19 model is used to solve the viscous incompressible NavierStokes equations for non-Newtonian fluids. The lattice Bolztamann D3Q7 model is used to solve for the constitutive equations (Oldroyd-B and FENE-P models). The new method is tested on two FSI toy problems. Numerical experiments indicate that the new method is conditionally stable and convergent with the first-order accuracy. The simualtion results suggest that the non-Newtonian nature of the fluid may deter the motion of the fluid, which is consistent with the existing literature.

Acknowledgement

The author thanks the US National Science Foundation(DMS-1522554) for the support.