Nonlinear thermo-structural behavior of sandwich panels with truss cores under through-thickness gradient temperature field

Wu Yuan, Hongwei Song,*, Chenguang Huang

a Key Laboratory for Mechanics in Fluid Solid Coupling Systems, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190,China

b School of Engineering Science, University of Chinese Academy of Sciences, Beijing, 100049, China

Keywords:

ABSTRACT A theoretical analysis is presented to predict the nonlinear thermo-structural response of metallic sandwich panels with truss cores under through-thickness gradient temperature field, which is a common service condition for metallic thermal protection system (TPS). The in-plane temperature distribution is assumed to be uniform, and through-thickness temperature field is determined by heat conduction. Two typical conditions are analyzed: nonlinear thermal bending in fixed inside surface temperature, and thermal post-buckling in fixed temperature difference between two surfaces. Temperature-dependent mechanical properties are considered, and gradient shear stiffness and bending stiffness due to non-uniform temperature is included. Results indicate that the temperature-dependent material properties obviously affect bending resistance;however, the effect is negligible on post-buckling behavior. Influences of geometric parameters on the thermo-structural behavior of the sandwich panel according to the present theoretical model are discussed.

Sandwich panels are mechanically efficient lightweight structures that are composed of two thin and stiff face sheets and a relatively thick and lightweight porous core. Recently sandwich panels with truss cores (SPTCs) have been received considerable attention [1-12]. This type of structure has achieved significant success in various practical fields, such as heat insulation,energy absorption, noise reduction, and electromagnetic wave shield [2, 5, 13-15]. When being used in a thermal protection systems (TPS) of high-speed flight, the outside surface is typically subjected to intense aerodynamic heating, whereas the inside surface is approximated to an adiabatic boundary condition.Therefore, SPTCs constantly experience a through-thickness gradient temperature field due to heat conduction. One of the undesirable effects of SPTCs under such loadings is thermal stress, which may lead to premature failure at temperatures below those that substantially impair material properties [16].Nonlinear thermal bending and thermal post-buckling are two main failure mechanisms in these conditions.

Ansari et al. [17] analyzed the nonlinear bending of a microplate based on Mindlin’s strain gradient elasticity and first-order shear deformation plate theory. Le-Manh et al. [18] presented an analytical solution for the nonlinear bending behavior of a composite plate with variable thickness. For sandwich panels,Rezaeifard et al. [19] investigated the bending behavior of sandwich beams with elastic-plastic cores. Several studies have focused on the bending of plate structures subjected to thermal loadings. Suresh and Mortensen [20] considered the large deformation analysis of graded multi-layered composites. They found that the nonlinear strain-displacement relation should be applied when thermal loading reaches a high level. Shen [21, 22]analyzed the nonlinear thermal bending response of functionally graded material plates by using a two-step perturbation method. Dong and Li [23] developed a unified model for bending, buckling, and vibration for temperature-dependent functionally graded rectangular plates subjected to thermal loadings.Aside from theoretical analysis, numerical studies, such as those that use the weak form quadrature element method [24], the meshless method [25], and the element free Galerkin method[26], have also been conducted to investigate the bending response of thin-walled structures.

Cetkovic [27] investigated the critical thermal buckling behavior of laminated plates by using the layerwise displacement model. Yuan et al. [12] obtained the critical buckling temperatures of SPTCs under fully clamped boundary conditions based on the Ressiner model, later on they built failure maps considering thermal buckling as one of the failure modes [9]. For thermal post-buckling response, Mossavarali and Eslami [28] studied the thermal post-buckling behavior of thin plates with initial flaws.Nikrad and Asadi [29] provided a theoretical solution for the thermal post-buckling behavior of delaminated composite plates based on the minimum potential energy principle. Shen[30] investigated the thermal post-buckling behavior of a functionally graded plate based on high-order shear deformation theory. Yuan et al. [10] studied the thermal post-buckling behavior of SPTCs under uniform thermal loadings.

Few studies have examined the thermo-structural response of SPTCs when experience through-thickness gradient temperature field, which is a typical thermal loading condition for TPS during service. In the present work, the nonlinear thermal bending and thermal post-buckling behavior of SPTCs under through-thickness gradient temperature field are investigated.Through-thickness heat conduction and temperature-dependent material properties are considered, and gradient shear stiffness and bending stiffness due to non-uniform temperature is incorporated in the theoretical model.

Theoretical model.As shown in Fig. 1(a), a rectangular simply supported metallic SPTC is considered. The length,width, and thickness of the SPTC are a, b, and hp, respectively.The thickness of the truss core is hc. The angle between the core member and the face sheet is. A uniform heat flux due to aerodynamic heating is loaded onto the outside surface, and the inside surface approximates to an adiabatic boundary condition,as shown in Fig. 1(b). The in-plane temperature distribution is assumed to be uniform, and through-thickness temperature field is determined by heat conduction. Two cases of thermal boundary conditions are considered.

Case 1. The temperature of the inside face sheet Tiis assumed to be constant. In this case, the temperature difference between the two face sheets increases when it heated. Therefore, thermal bending is observed as the main failure mode.

Case 2. The temperature difference between the outside and inside face sheets To− Tiis assumed to be constant. The thermal bending moment remains unchanged when the temperature of the SPTC varies. Hence, thermal post-buckling is the main failure mode.

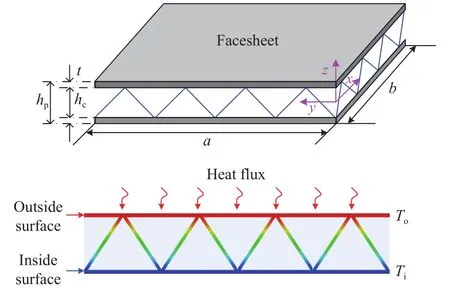
Fig. 1. Schematic of SPTCs under through-thickness gradient temperature field.

The through-thickness gradient temperature distribution can be obtained by solving a steady-state heat transfer equation as follows:

The temperature distribution along the thickness of the face sheet is assumed to be uniform due to low thickness. Then, the temperature along the lengthwise direction of the truss member is solved by imposing the boundary conditions T = Tiat Z = −hc/2 and T = Toat Z = hc/2 as follows:

The nonlinear equilibrium equations for SPTCs can be obtained by using the minimum potential principle, which can be expressed as

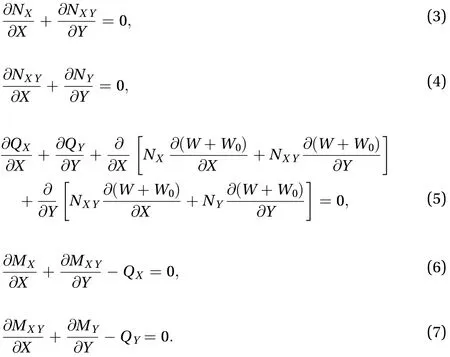
The temperature-dependent material properties of the SPTC are considered, which can be written as

where T is the temperature. The internal force is

where C and D are the shear stiffness and flexural rigidity of the sandwich panel, respectively.

The shear stiffness of the SPTC is derived by the equivalent shear deformation of a one-unit cell, as shown in Fig. 2. When the variation of the elastic modulus along the lengthwise direction of the truss member is considered, the truss core deformations of the pyramidal, tetrahedral, and Kagome configurations can be expressed as

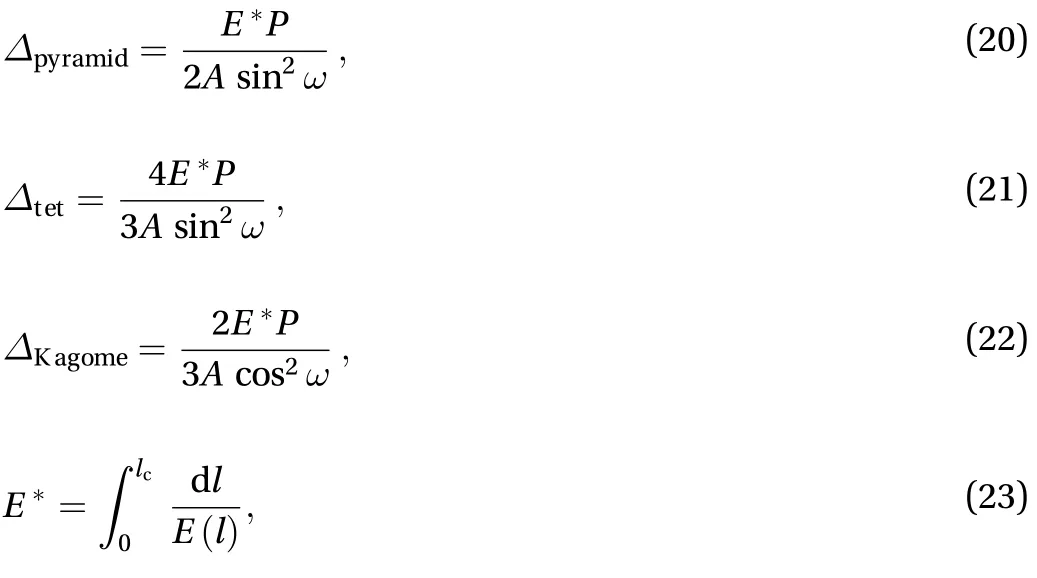
where A is the cross-sectional area of the truss member. The equivalent shear deformation of the truss cores subjected to a non-uniform thermal loading can be obtained as follows:

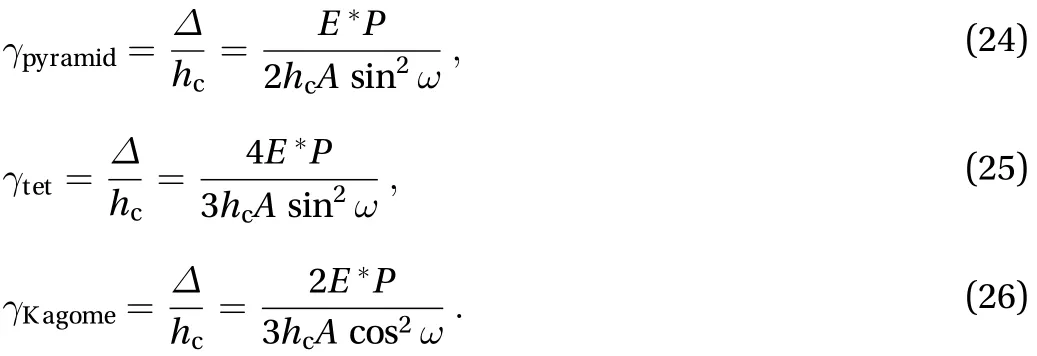
Then, the equivalent shear modulus of the truss cores can be expressed as

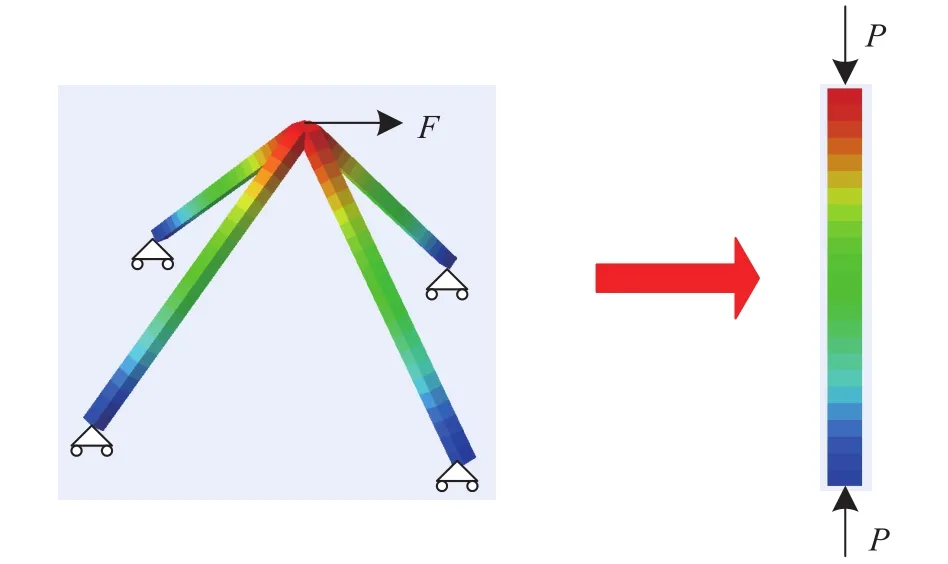
Fig. 2. Schematic of the thermal mechanical deformations of the pyramidal truss core member.

The relative density is

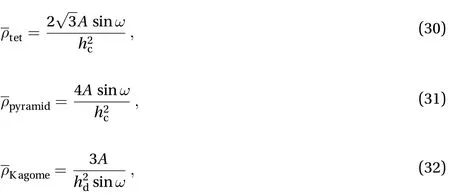
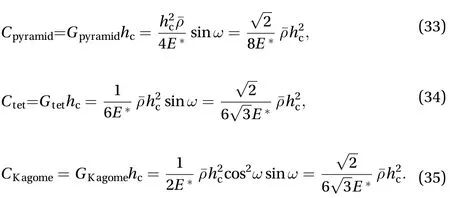
Analytical method.When stress functions and deformation compatibility are considered, the dimensionless differential governing equations for the SPTC subjected to non-uniform through-thickness loadings can be obtained by introducing the dimensionless quantities used in Ref. [10].

Equations. (36)–(39) can be solved by applying the two-step perturbation technique used in Ref. [30]. The solutions for the unknown functions are assumed to have the following forms:

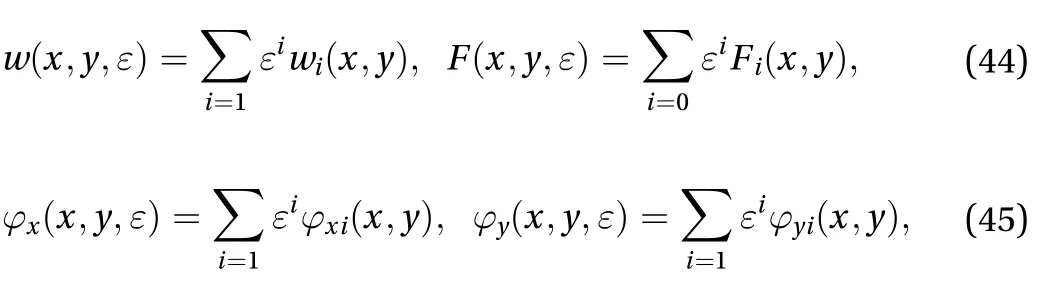
The initial global geometric imperfection of the SPTC can be expressed in the following form:

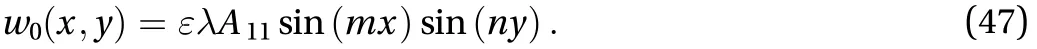
Equations. (44)–(45) can be solved by substituting Eqs.(43)–(47) into Eqs. (36)–(39) and collecting terms with the same order as.

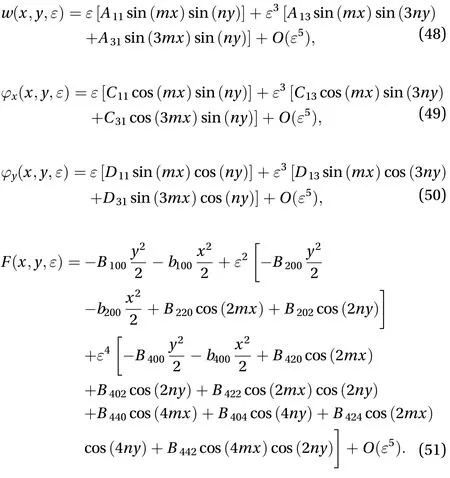
The symbols used in Eqs.(48)-(51) are described in Appendix A.

When Eqs. (48)–(51) is substituted into the simply supported boundary conditions, the equilibrium path of the SPTC subjected to non-uniform through-thickness heating can be obtained by

All the symbols used in Eq. (52) are described in Appendix B.

The theoretical results of the response of SPTCs subjected to non-uniform through-thickness heating are presented here. The mechanical properties of a metallic material are degraded with an increase in temperature. Therefore, temperature-dependent material properties are considered in the theoretical model. In the present study, stainless steel is selected for the SPTC. The elastic modulus of stainless steel can be expressed as a quadratic function of temperature as follows:

where P0, P1, and P2are the coefficients of the quadratic function, as shown in Table 1. The thermal expansion coefficient of stainless steelis 1.7×10−5°C−1. To obtain the response of SPTCs with temperature-dependent materials, Eq. (52) is solved using an iterative numerical procedure. Then, the effects of geometric and material properties on the nonlinear thermal bending and thermal post-buckling behavior of SPTCs are investigated.

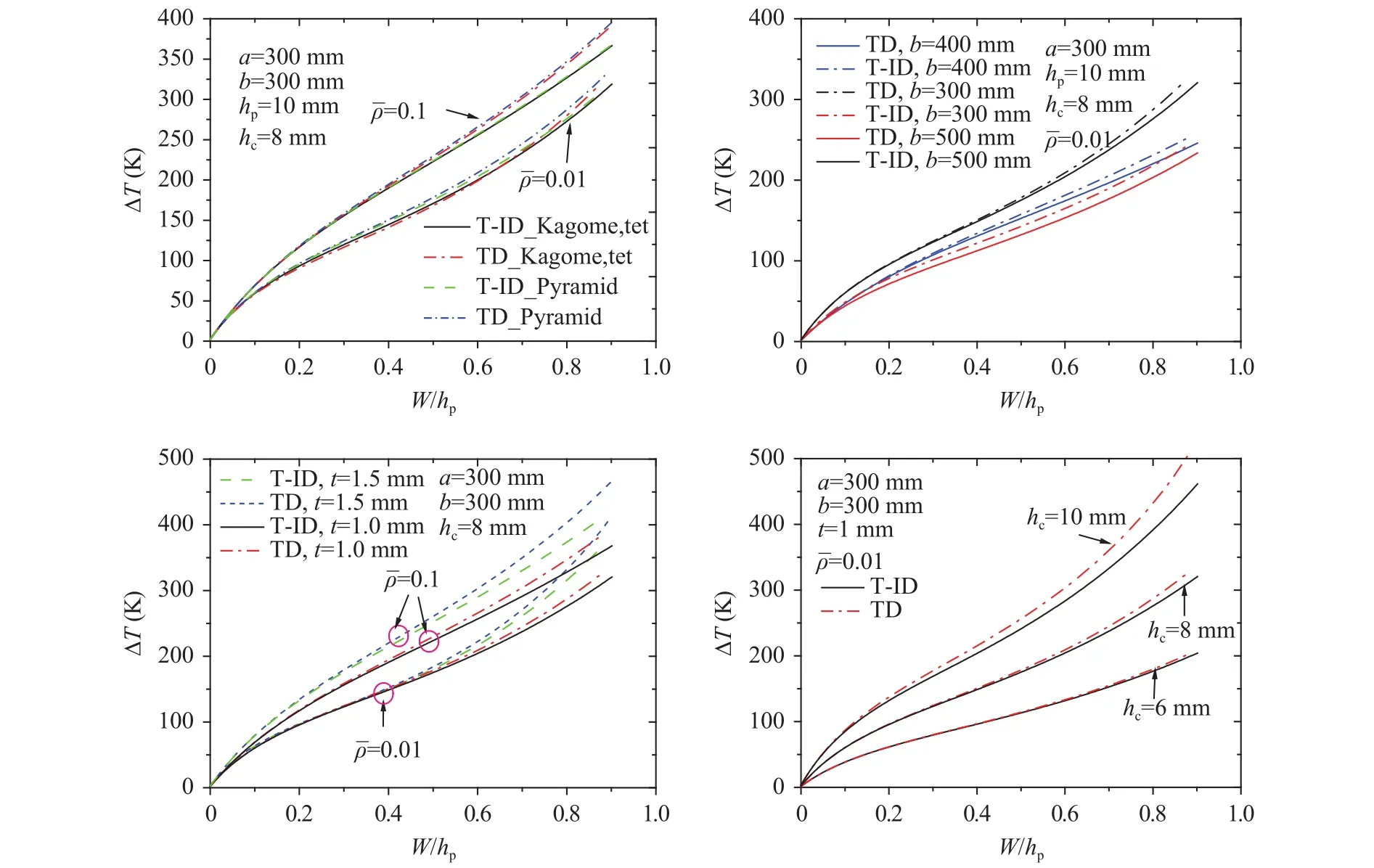
Fig. 3. Effect of geometric parameters on the nonlinear bending behavior of SPTCs under through-thickness gradient temperature field,Ti = 20°C.

Nonlinear thermal bending.Figure 3 shows the effect of geometric parameters on the nonlinear thermal bending behavior of SPTCs with different configurations. “TD” denotes SPTCs with temperature-dependent materials, whereas “T-ID” denotes temperature-independent materials. In Case 1, the temperature of the inside surface is assumed to be constant, which is 20°C,whereas the temperature of the outside surface increases with an increase in heat flux irradiation time. Under this condition,indicates the temperature increase of the outside face sheet. The in-plane force produced by thermal stresses in the outside face sheet will decrease when temperature-dependent material properties are considered, whereas the stiffness of the inside surface will remain in its initial state. Consequently, the bending deformation of the SPTC with TD materials is smaller than that of the SPTC with T-ID materials when they exhibit the same temperature increase, as shown in Fig. 3(a).

As indicated in Eq. (33)–(35), the shear stiffness of the SPTC is proportional to relative density. Therefore, increasing relative density will increase the stiffness of the SPTC under thermal bending. Among the three configurations, the shear modulus of the SPTC with a pyramidal truss cores is larger than those of the two other configurations. Consequently, bending resistance of the sandwich panel with pyramidal truss cores under nonlinear bending is the highest among the three configurations. However,the difference among the three configurations is not evident when relative density increases.

As shown in Fig. 3(b), aspect ratiosignificantly affects the nonlinear thermal bending behavior of the SPTC. The slenderness ratio of the SPTC is increased with an increase in aspect ratio. Therefore, the stiffness to thermal bending is decreased.The variation in thickness may significantly affect the flexural stiffness and in-plane load of the SPTC. Consequently, the effect of face sheet thickness on the bending behavior of the SPTC dif-fers when relative density varies. As shown in Fig. 3(c), the stiffness under thermal bending of the SPTC with a thicker face sheet is evidently higher even under a small thermal loading when relative density is 0.1. However, the shear stiffness of the SPTC is lower when relative density decreases to 0.01. In such case, increasing the thickness of the face sheet will simultaneously increase the in-plane compressive force. Therefore, the bending resistance of the SPTC is not increased significantly.Figure 3(d) shows the effect of sandwich panel thickness hcon the nonlinear thermal bending behavior of the sandwich panel with pyramidal truss cores. The results indicate that the bending resistance of the SPTC is improved when the thickness of the sandwich panel is increased.

Thermal-post buckling.In Case 2, a fixed through-thickness temperature increase is observed anddenotes the temperature increase of the sandwich panel. If temperature-dependent material properties are considered, then the thermal bending moment is decreased when the temperature rise of the SPTC increases. Therefore, thermal post-buckling will be the main failure mode under this type of thermal boundary condition.

Figure 4 shows the thermal post-buckling behaviour of the SPTC under different relative densities. Unlike in the nonlinear thermal bending behavior, the elastic modulus of the two face sheets decreases when temperature increases. The degradation of the in-plane force and stiffness of the SPTC can be canceled out. Therefore, the post-buckling deformation of the SPTC with TD materials is in accordance with that of the SPTC with T-ID materials, as shown in Fig. 4(a). In addition, the buckling deformation of sandwich panels with pyramidal truss cores is smaller than those of the other two configurations when they have the same relative density. Similarly, the thermal buckling deformation of the SPTC with a relative density of 0.1 is smaller than that of the SPTC with a relative density of 0.01. Figure 4(b)shows the effect of temperature gradient on the thermal postbuckling behavior of SPTCs. SPTCs will exhibit an initial bend-ing deformation at the onset due to the thermal bending moment induced by the initial through-thickness temperature gradient. Therefore, the initial temperature gradient will considerably influence the buckling behaviour of SPTCs.

The bending resistance is decreased with an increase in the length of one side of the SPTC, as shown in Fig. 4(c). Similar to thermal bending response, the effect of face sheet thickness on the thermal post-buckling behavior of the SPTC subjected to non-uniform through-thickness heating differs when relative density varies. Figure 4(d) shows that the stiffness of the SPTC with a thicker face sheet is higher when relative density is 0.1.However, an increase in thickness may reduce bending resistance of the SPTC when relative density decreases to 0.01. Figure 4(e) shows the effect of sandwich panel thickness hcon the thermal post-buckling behaviour of the SPTC. Equation (18) indicates that the flexural stiffness of the SPTC is significantly increased with an increase in thickness. Therefore, the the thermal post-buckling resistance can be improved by using a thick sandwich panel.

The response of simply supported SPTCs under throughthickness gradient temperature filed is investigated theoretically.The nonlinear equilibrium equations for SPTCs are developed by applying the minimum potential energy principle. The equilibrium path is obtained by using the perturbation approach.Nonlinear thermal bending and thermal post-buckling are evaluated. The effects of geometric and material properties on the response of the SPTC are investigated. The deformation of the SPTC is small for the thermal bending behavior when temperature-dependent properties are considered. Meanwhile, temperature-dependent properties have minimal effects on the thermal post-buckling behavior. The stiffness of the sandwich panel with pyramidal truss cores is higher than those of the Kagome and tetrahedral configurations. The SPTC under thermal bending and post-buckling resistance can be improved by applying a high relative density. The stiffness of the SPTC subjected to nonuniform through-thickness heating is increased with an increase in sandwich panel thickness. The effect of face sheet thickness differs when relative density varies.

Acknowledgments

The financial support from the National Natural Science Foundation of China (91016025, 11472276, 11602271, and 11332011) and the Defense Industrial Technology Development Program of China (JCKY2016130B009) is gratefully acknowledged.

Appendix A

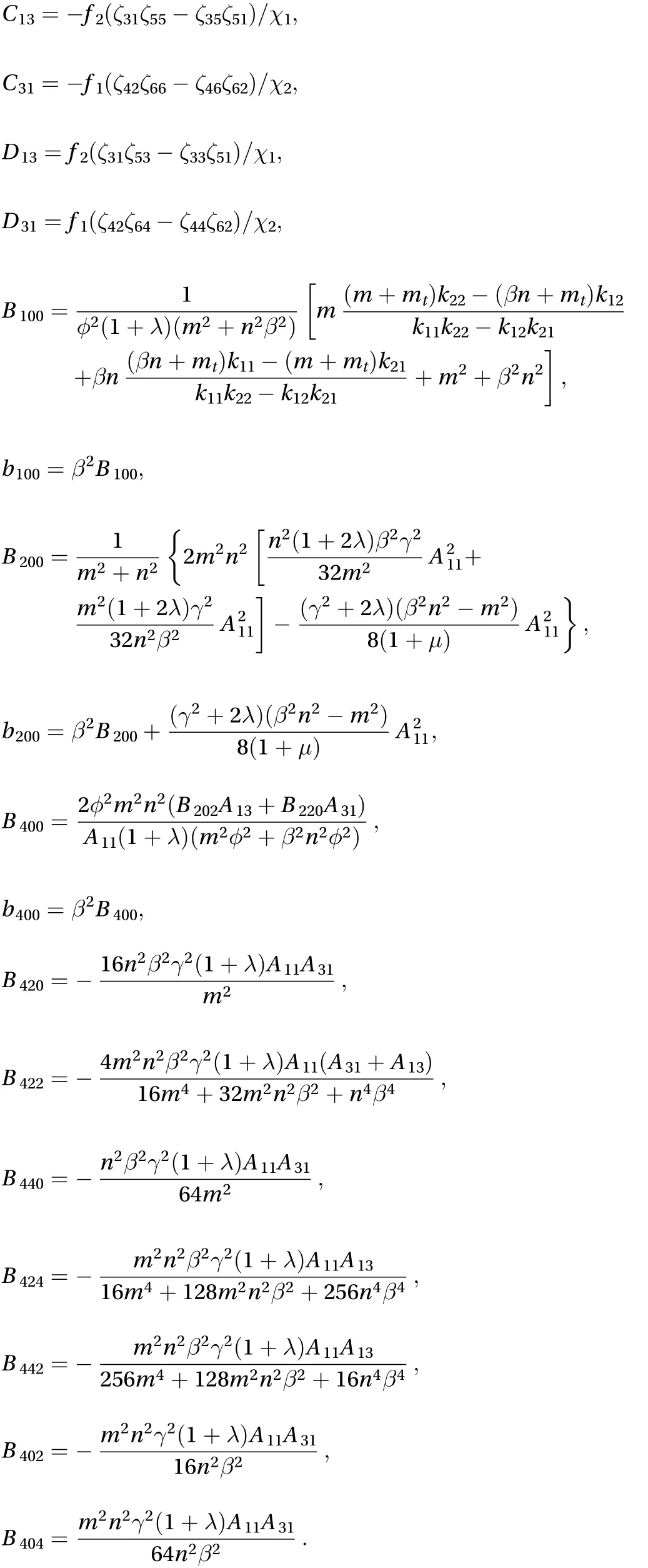
Appendix B