“反思”在解题中的“升华”——培养学生反思意识,提高数学素养

广东 刘 伟

荷兰著名数学家弗赖登塔尔曾指出：“反思是数学思维活动的核心和动力，通过反思，才能使现实世界数学化.”数学学习过程其实就是一个思考问题解决问题的过程，通过解题，加深对基础知识、学习方法、解题策略的理解和掌握，反思则是对这些活动进行再一次加工，从中总结经验教训或发现新的问题，更好地指导未来的数学学习活动，促进数学知识的吸收，提高学生数学学科素养.因此,将“反思”融入到审题、解题、纠错、归纳等过程中,势在必行.笔者在实际教学过程中,有意识地培养学生的反思意识,从而使得学生的数学学科素养得以提高.

1.反思审题过程,提升审题能力

审题能力是学生思维能力的一个重要方面,审题能力的高低直接影响学生解题的速度与水平.在实际教学过程中,笔者发现很多学生因为审题不清而失分.

2．反思解题思路，培养学生思维的广阔性

文学作品解读常有这样一句话:一千个读者,便有一千个哈姆雷特.数学学科亦应重视学生的发散思维能力的培养.而在我们重视引导学生一题多解的思维习惯的同时也应该加强反思意识培养.对于同一道数学题目，知识掌握程度的不同，审题角度的不同，不同学生会给出不同的解题方案，就算同一个学生也可能给出两到三种解答过程，教师要引导学生对这道题目进行反复思考，解完一道题后不能停留在所得出的结论上，应引导学生重现思路.此时，教师应向学生提出引导性的问句，如：你是怎么想的？为什么这样想？这样做你想解决哪个问题？这样做能达到你的预期目标吗？达到了，你有没有更好的想法？达不到，你又该如何？用这种层层递进的发问方式使得学生的思维一步步展开，重现学生自己的思维过程并进一步要求学生根据题目的现有已知条件，进行多角度观察、联想，找到更多的思维通道，涉及到更丰富的数学知识点，去探索最佳的解题途径.

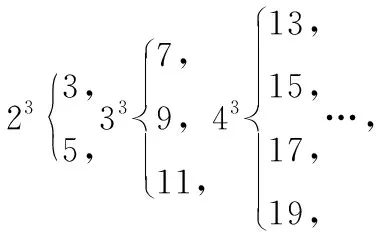
老师：看了题同学们有什么想法？

学生1：我发现这个规律，即

第一个式子可化为3+5=23，连续2个奇数之和为23，

第二个式子可看成连续3个奇数之和为33,即7+9+11=33，

从而，猜想连续m个奇数之和为m3，

而73是除1之外第36个奇数，

又因为2+3+4+…+m-1<36，

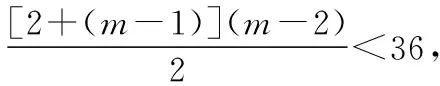
m2-m<74，解得m=9满足条件.

学生2：我想把它变个形式：

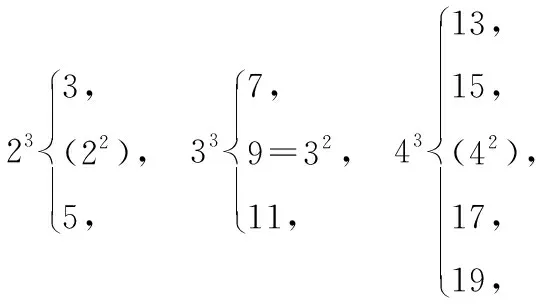
通过观察,发现每列数的中间位置通过添数(偶数的立方)或者改写(奇数的立方)，就很容易看到规律.即合成数是某数的立方则其分裂数组中的中位数是该数的平方,分裂数组是偶数个数的,中间插入该数的平方；是奇数个数的,把中间奇数改写成该数的平方.又因为82=64,而83这组“分裂”成连续8个奇数之和,它们分布在82的上下两侧如下:

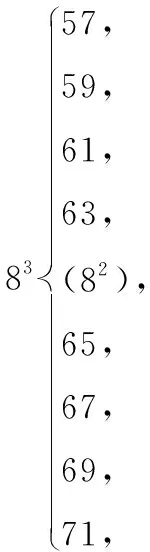
所以m=9.

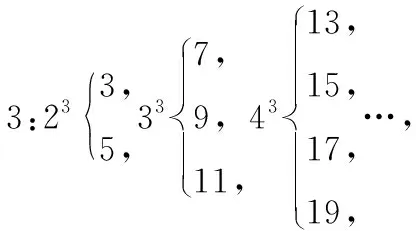
其中5=22+2-1，11=32+3-1，19=42+4-1，…，猜想73趋近于m2+m-1，

当m=8时，m2+m-1=71，故m=9.

三个学生从三个不同的视角诠释了这道题，学生在再一次审视这道题的过程中，不但掌握了观察法，估值法，排除法，还有了思维能力的提升,如归纳思想，趋近思想等等，一道题，不同的途径，相同的结果，不同的效率，不同知识点的应用，值得再次反思，从中整理思路，提高思考能力.而在高中人教版选修2-2推理证明这一章节中一个立方数或一个平方数“分裂”成多个连续的奇数或偶数或自然数,求合成数或“分裂数”中的成员数,抑或是已知“分裂数”中的成员数求合成数,或求其他某个指定位置成员数等等这样的一类题型都需要学生掌握这些方法和技巧并融会贯通，灵活应用.

又如:对大于或等于2的正整数的幂运算有如下分解方式：

22=1+3,32=1+3+5,42=1+3+5+7,…；

23=3+5,33=7+9+11,43=13+15+17+19,….

根据上述分解规律，若m2=1+3+5+…+11,p3的分解中最小的正整数是21，则m+p=________.(答案:11)

通过一题多解，训练学生发散思维,熟悉不同章节的知识点.反思解题思路，有利于培养学生思维的广阔性和灵活性.

3．反思易错之处，增强学生纠错能力

黑格尔说“错误本身乃是达到真理的一个必然的环节.”正确可能被模仿，可错误却绝对是经历.反思，让学生再次“场景重现”体会错误之处，找到错误的根源，避免重复错误.通过对错解进行分析和纠正，对已有知识重新认识，可以加深对知识点和概念的解读，弥补自己知识体系的漏洞,增强学生纠错能力.

3.1概念理解错误

高中数学课很多都是由概念定义课组成，学生理解这些概念往往比较片面.如下面的等差数列的概念练习题.

例3“an+1+an-2=an+an-1(n∈N*且n≥3)”是“数列{an}为等差数列”的

( )

A．充分不必要条件

B．必要不充分条件

C．充要条件

D．既不充分也不必要条件

学生失误在自己的惯性思维，认为只要an+1-an=an-1-an-2(n∈N*且n≥3)就是等差数列，而忘记了摆动数列!例如:0,1,0,1,0,1，…，当n为奇数时,an+1-an=an-1-an-2=1;当n为偶数时,an+1-an=an-1-an-2=-1，即“an+1+an-2=an+an-1(n∈N*且n≥3)”推不出“数列{an}成为等差数列”,反之,“数列{an}成为等差数列”可以推出“an+1+an-2=an+an-1(n∈N*且n≥3)”，因此，答案是B.

高中数学概念如:独立事件,互斥事件,独立重复试验,二项分布,函数的零点,极值点,极值等等,学生理解这些概念常常存在一些问题,教师应对学生在概念、定理等易出错的地方给予一定地引导，让学生对自己的盲点，遗漏点，自以为是点进行及时地整理，避免一错再错，培养学生重新修补知识漏洞的习惯，储备一些典型的错误例子用以弥补学生知识的不足，对学生是一个很好的提升,反思概念混淆之处，加深对概念的理解.

3.2知识点应用错误

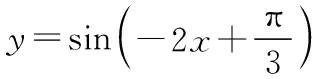
对于较为复杂的知识点如复合函数的单调性,奇偶性,分段函数的零点问题等等,教师授课时不妨试试“示错”教学法,让学生在错误中找到错误原因,加强对知识点的应用.

4.反思思路断点之处，提升学生应变能力

魏晋陶渊明《桃花源记》中记载：“林尽水源，便得一山，山有小口，仿佛若有光.便舍船，从口入.初极狭，才通人.复行数十步，豁然开朗.”如学生做题，先有疑，后寻解.学生做题过程中经常会遇到伸手达不到的地方，会意识到“此路不通”，以至于思考停顿不前，一片空白.教师在讲授时应对“断点”巧加工,恰当设置一些有利于问题发展的“陷阱”，让学生在教师的启发下，延续思路，改变思维，达到柳暗花明的效果.同时,要求学生对自己的断点进行必要的整理.培养学生的解题能力和应变能力.

例5(2016·山东卷文·20)设f(x)=xlnx-ax2+(2a-1)x，a∈R.

(Ⅰ)令g(x)=f′(x)，求g(x)的单调区间；

(Ⅱ)已知f(x)在x=1处取得极大值,求实数a的取值范围．

【解】(Ⅰ)由f′(x)=lnx-2ax+2a，

可得g(x)=lnx-2ax+2a，x∈(0，+∞)．

当a≤0时，

x∈(0，+∞)时，g′(x)>0，函数g(x)单调递增；

当a>0时，

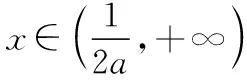
所以当a≤0时，g(x)的单调增区间为(0，+∞)；

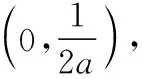
(Ⅱ)由(Ⅰ)知，f′(1)=0.

①当a≤0时，f′(x)单调递增，

所以当x∈(0，1)时，f′(x)<0，f(x)单调递减；

当x∈(1，+∞)时，f′(x)>0，f(x)单调递增．

所以f(x)在x=1处取得极小值，不合题意．

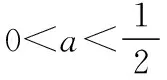
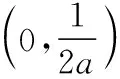
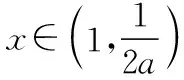
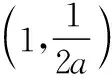
所以f(x)在x=1处取得极小值，不合题意．

所以当x∈(0，+∞)时，f′(x)≤0，f(x)单调递减，不合题意．

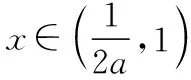
当x∈(1，+∞)时，f′(x)<0，f(x)单调递减，

所以f(x)在x=1处取得极大值，符合题意

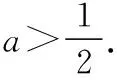
对于第二问,绝大部分学生只能望而却步,作为老师我们又如何引导呢?其实第一问就给了我们想像的空间f′(x)=lnx-2ax+2a，把f′(x)=lnx-2a(x-1)联想经典函数lnx≤x-1,当且仅当x=1时等号成立.用数形结合岂不是更妙.

大体思路如下：

第2问是已知f(x)在x=1处取得极大值．求实数a的取值范围．

由问题可知函数f(x)要在x=1处取得极大值,等价于函数f′(x)=lnx-2a(x-1)在x=1左边符号为正,右边为负,即“先正后负”,进而可知,在x=1的左边函数y=lnx的图象应在函数y=2a(x-1)的上方;在x=1的右边函数y=lnx的图象应在函数y=2a(x-1)的下方,作图可知，直线y=x-1是函数y=lnx在x=0处的切线.函数y=lnx的图象在直线y=x-1的图象下方,直线y=2a(x-1)与直线y=x-1都过点(1,0),所以,只要直线y=2a(x-1)的斜率大于直线y=x-1的斜率,问题就得以证明了.

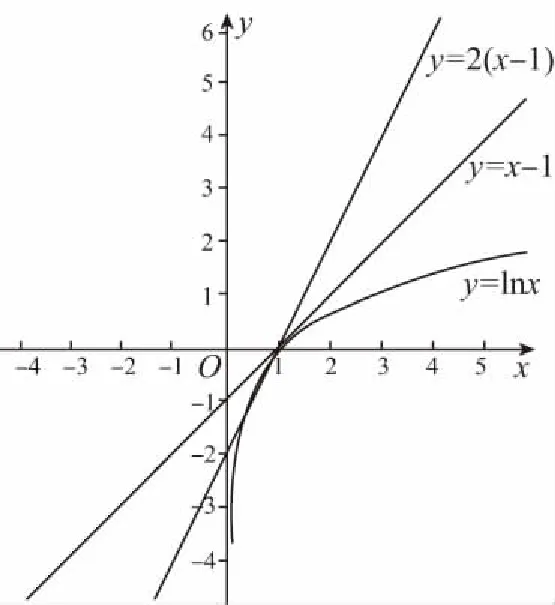
另一种方法,因为函数f(x)要在x=1处取得极大值,就等价于函数f′(x)=lnx-2a(x-1)在x=1左边符号为正,右边为负,即“先正后负”,又因为f′(1)=0，

所以函数f′(x)在x=1处的斜率必然小于零.

一个题在断点时往往会给我们不同的数学期望，只要我们能紧抓数学概念，以形助数，就会给学生不一样的数学惊喜.

5.反思类似题目，发现知识内在联系

同一类型的数学问题，其求解方法往往有规律性，解完一道题要学生思考此题是否可作一般性推广和引申，这样学生能解决的就不是一道题，而是一类题.如上面讲的例5.求含参函数的最值这一类问题，我们可以直接求函数的最值，也可以分离参数，或者可以转换变量，还可以数形结合，既加强了对多种数学思想方法的融会贯通，又给出了这一类题的普遍解法，这里思维运转之快，思路步骤之多，学生课后或练习后若不好好反思，岂能掌握，但细细品尝，慢慢消化，又何止收益点滴.

6.反思解题结果，培养学生数学思维的深刻性

事实上,就问题解决的周期而言,问题是问题解决的始端,而一个问题的解决往往孕育着一个新问题的产生.做完一道题后,教师应指导学生思考该题的结果.波利亚的题后反思即他的《怎样解题》中回顾环节对此进行了精彩的论述：你能检验这个结果吗？你能检验这个论证吗？你能以不同的方式推导这个结果吗？你能一眼就看出它吗？你能利用它的结果吗?你能利用它的方法吗?为了能够利用它,你是否应该引入某些辅助元素?这样的反思,有助于提高高中生数学学科的自我监控能力,培养学生数学思维的深刻性.

例6已知函数f(x)=alnx-x+1(a∈R)．

(Ⅰ)求f(x)的单调区间;

(Ⅱ)若f(x)≤0在(0,+∞)上恒成立，求所给实数a的值;

初看这个题目学生会被第(Ⅲ)问给难住，毕竟高三一轮复习中我们很少给出这样的题.由于(Ⅰ)(Ⅱ)问较简单，笔者这里只给出第(Ⅲ)问的解法.

教师：由前面两问，我们知当a=1时f(x)≤0在(0,+∞)上恒成立，即lnx-x+1≤0⟹lnx≤x-1,

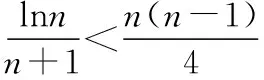
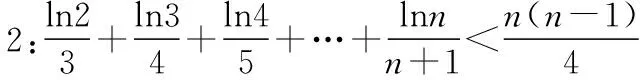
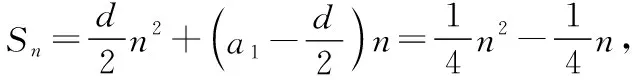
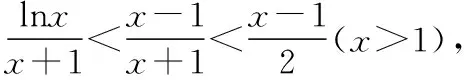
教师：很好，学生由题目的结果出发，回到题目的条件，再由条件出发,解决问题,不错的想法，数学的综合分析法应用得很恰当,那还有没有其他方法？

学生4：能不能用数学归纳法，然后和函数结合起来.

(1)当n=2时，不等式成立,

[编者按]本文为原创团队教师将教研中关于原创试题的命制思路及感悟总结归纳，与读者分享.以期对教师命题活动有所启发或帮助.