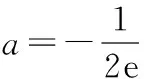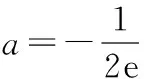“超级全能生”2018高考全国卷26省12月联考乙卷数学(理科)

一、选择题：本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.

1.设集合A={x|x2-x-6<0},B={x|2x<1},则A∩B=

( )

A.(-∞,3) B.(0,3)

C.(-2,3) D.(-2,0)

2.已知i为虚数单位,zi=1+5i,则复数z的共轭复数为

( )

A.1+5i B.1-5i C.5+i D.5-i

( )

4.夜跑是比较流行的一项健身运动,某地政府围绕边长为400米的正方形湖泊修建了一条跑道,甲、乙两人各自围绕湖泊进行夜跑,当甲跑到正方形跑道的一个顶角,此时乙距离甲的距离大于500米的概率等于

( )

( )

6.(x-3y)(x-2y)6的展开式中x4y3的系数为

( )

A.-80 B.-40 C.40 D.-340

7.魏晋时数学家刘徽在他的著作《九章算术注》中,称一个正方体内两个互相垂直的内切圆柱所围成的几何体为“牟合方盖”.刘徽通过计算得知正方体的内切球的体积与“牟合方盖”的体积之比为π∶4；若已知正方体的棱长为2,则“牟合方盖”的体积为

( )

8.如图,程序框图所描述的算法是计算斐波那契数列中的项,若输入的k=20,则输出n的值为

( )

A.7 B.8 C.9 D.10

( )

A.5

C.6

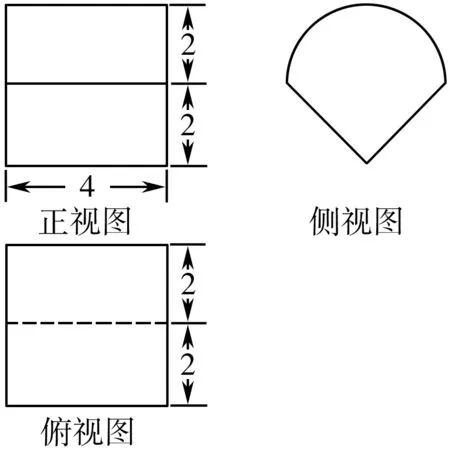
10.某几何体的三视图如图所示,则该几何体的表面积为

( )

( )

12.若函数f(x)=ex与函数g(x)=-x2+2x+a(x<0)有公切线,则实数a的取值范围是

( )

A.(-∞,2-2ln2) B.(-1,-2ln2)

C.(-∞,-1) D.(-∞,ln(2e))

二、填空题：本题共4小题,每小题5分,共20分.

三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.

(一)必考题：共60分.

17.(12分)

已知函数f(x)=x2-5x+1,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在f(x)的图象上.

(Ⅰ)求{an}的通项公式；

(Ⅱ)求数列{n·2an}的前n项和Tn.

18.(12分)

如图,在以A,B,C,D,E,F为顶点的五面体中,四边形ABCD为等腰梯形,四边形ABFE为矩形,且平面ABFE⊥平面ABCD,BC=CD=AE=1,AB=2.

(Ⅰ)求证:平面BDF⊥平面ADE；

(Ⅱ)求二面角B-DF-E的余弦值.

19.(12分)

2017年5月,来自“一带一路”沿线的20国青年评选出了中国的“新四大发明”：高铁、支付宝、共享单车和网购.共享单车的产生使得城市交通“最后一公里”出行难题有望进一步改善,共享单车的火热也带动了自行车行业的迅猛发展,产能、质量、设计成为共享单车考量合作自行车厂商的主要标准.已知某自行车厂生产不同规格的一种自行车零件,根据检测标准,其合格产品的质量y(g)与尺寸x(mm)存在一定关系,现收集了7组观测数据列于下表中,并作出散点图如下.

x20222426283032y610212464113322z=lny1.792.303.043.184.164.735.77

参考数据：

xyz∑7i=1(xi-x)2∑7i=1(zi-z)(xi-x)26803.5711235.84

(Ⅰ)直接根据散点图判断,y=a+bx与y=ec+dx哪一个适宜作为质量y(g)与尺寸x(mm)的回归方程类型？

(Ⅱ)根据(Ⅰ)的判断,求y关于x的回归方程；

20.(12分)

已知动圆P过点A(2,0),且被y轴截得的线段长为4,记动圆圆心P的轨迹为曲线C.

(Ⅰ)求曲线C的方程；

21.(12分)

已知函数f(x)=xex+a(x+1)2(其中e为自然对数的底数).

(Ⅰ)求函数f(x)的单调区间；

(二)选考题：共10分.请考生在第22,23题中任选一题作答.如果多做,则按所做的第一题记分.

22.[选修4-4：坐标系与参数方程](10分)

(Ⅰ)求圆C的直角坐标方程；

(Ⅱ)若直线l与圆C交于A,B两点,求弦长|AB|.

23.[选修4-5：不等式选讲](10分)

已知函数f(x)=|2x+1|+|x-1|.

(Ⅰ)求不等式f(x)≥3的解集；

参考答案

1.D2.C3.C4.D5.C6.D7.C8.B9.B

17.解：(Ⅰ)因为(n,Sn)在函数f(x)的图象上,

所以Sn=n2-5n+1.

当n=1时,a1=S1=1-5+1=-3；

当n≥2时,an=Sn-Sn-1=n2-5n+1-[(n-1)2-5(n-1)+1]=2n-6,

当n=1时,a1不满足an=2n-6,

(6分)

当n=1时，T1满足题意.

(12分)

18.解：(Ⅰ)证明：因为四边形ABFE为矩形,

所以EA⊥AB,

由平面ABFE⊥平面ABCD,所以EA⊥平面ABCD,

又BD⊂平面ABCD,所以EA⊥BD.

过点D作DG⊥AB交AB于点G,

所以∠ADB=90°,即AD⊥BD.

由AD∩AE=A,所以BD⊥平面ADE.

由BD⊂平面BDF,所以平面BDF⊥平面ADE.

(5分)

(Ⅱ)以A点为坐标原点,AB所在直线为y轴,AE所在直线为z轴,建立空间直角坐标系A-xyz，如图所示,

设n1=(x,y,z)为平面EDF的法向量,

设n2=(x1,y1,z1)为平面BDF的法向量,

(12分)

19.解：(Ⅰ)根据散点图判断,y=ec+dx更适宜作为质量y(g)与尺寸x(mm)的回归方程类型.

(3分)

(Ⅱ)设y=ec+dx,z=lny,则z=c+dx,

所以y=e0.32x-4.75.

(7分)

(Ⅲ)由表中数据知,x可取20,22,24,26,即抽取的7件合格产品中优等品有4件,所以ξ的可能取值是0,1,2,3.

所以ξ的分布列为

ξ0123P13512351835435

(12分)

20.解：(Ⅰ)设动圆圆心的坐标为P(x,y),

由题意可得22+x2=(x-2)2+y2,化简得y2=4x,

所以曲线C的方程为y2=4x.

(4分)

当y0>0时,y1=y0-2,y2=y0+2,

当y0<0时,y1=y0+2,y2=y0-2,

(12分)

21.解：(Ⅰ)因为f(x)=xex+a(x+1)2,

所以f′(x)=(x+1)ex+2a(x+1)=(x+1)(ex+2a),

①当a≥0时,ex+2a>0,

令f′(x)>0,解得x>-1；令f′(x)<0,解得x<-1；

令f′(x)>0,解得x>-1或x

令f′(x)<0,解得ln(-2a)

令f′(x)>0,解得x>ln(-2a)或x<-1；

令f′(x)<0,解得-1

综上，当a≥0时,f(x)的单调递增区间是(-1,+∞)，单调递减区间为(-∞,-1)；

(5分)

(Ⅱ)证明：由(Ⅰ)可知,当a>0时,f(x)在区间(-1,+∞)上单调递增,在区间(-∞,-1)上单调递减,不妨设x1<-1

令F(x)=f(x)-f(-2-x)

=xex+a(x+1)2-[(-2-x)e-2-x+a(-x-1)2]

=xex+(x+2)e-2-x(x<-1),

因为F′(x)=(x+1)(ex-e-x-2)>0,

所以F(x)在(-∞,-1)上单调递增,

所以F(x)

所以f(x)

所以f(x2)=0=f(x1)

因为-2-x1>-1,x2>-1,f(x)在(-1,+∞)上单调递增,所以x2<-2-x1,

(12分)

22.解：(Ⅰ)圆C的极坐标方程为ρ=4cosθ,

可化为ρ2=4ρcosθ,

可得其直角坐标方程x2+y2-4x=0,

即(x-2)2+y2=4.

(5分)

设A,B对应的参数分别为t1,t2,

(10分)

故f(x)≥3的解集为{x|x≤-1或x≥1}.

(5分)

(10分)