三角试题中的“美丽”错误及心理学层面探因

山东 耿瑞照

数学解题过程是对数学题目从直观认知到思维分析再到尝试解答的复杂过程，邵瑞珍版本的《教育心理学》中对教学作了如下描述：“学习者需要重新组织若干已知的规则，形成新的高级规则，用以达到一定的目标”．笔者在三角部分教学中发现，学生解三角题的常见错误有三类，一是没有形成有效的解题思路；二是思维过程完全正确但运算出错；三是形成了一定的解题思路但思路中存在不易觉察的漏洞．犯第一类错误的学生通常数学基础较弱，需全方位提升数学基础才行；犯第二类错误的学生通常基础较好，只要提升解题的专注度就会避免此类错误；犯第三类错误的学生往往觉察不出自己的答案是错的，说明学生在解题思维上存在误区，这类错误更值得重视．本文将分析几种常见的错误，从教育心理学层面探究出错误原因，揭示题目本质，让错误也可以成为一种提升自我的资源．

1.数学元认知不足

数学元认知就是对数学认知活动的认识和监控，是在数学思维过程中表现出来的，以一定的数学观念为指导，对自己的思维过程的意识进行调节与控制．很多学生对数学元认知不足，体现在看到试题时看不出命题目的、形成不了解题思路；也有的学生对于讲过的“旧题”非常擅长，但一遇到“新题”就无从下手，缺乏知识迁移的能力．

【例1】已知三角形的三边长是三个连续的整数，最大角是最小角的两倍，求此三角形的最小边的长．

【分析】笔者在让学生解答本题时，发现有近八成的学生没有思路、不能解答．有些学生认为在解三角形时，必须明确告诉三角形六个元素中的三四个元素才行；对于这样一个没有数字甚至没有字母的问题就觉得无从下手，这其实是对正余弦定理理解不透彻造成的．

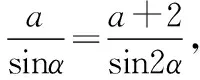
由①②解得a=4，所以最小边长是4．

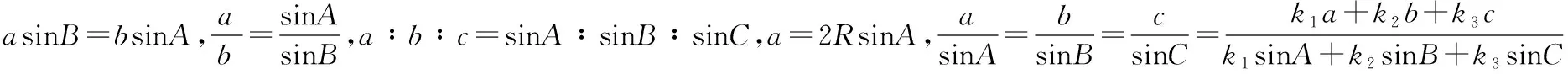
2.求易心理影响

求易心理，是指对于一些看似较为简单的问题，学生通常凭借直观认识得到较为简单但不够严密的解题方法，此时学生往往有放弃严密逻辑论证的心理倾向．求易心理在数学解题中的直接表现就是忽视隐含条件．

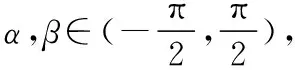
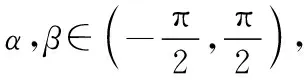
3.感知定向致误

感知定向是指个体在遇到客体之前在头脑中先于客体形成的定向思维，也称感知.这种感知存在于主体的头脑里，并影响主体对客体的感知.常见的表现就是先入为主的思想.

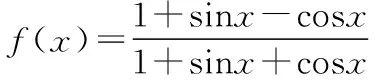
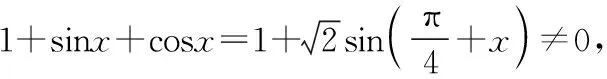
4.知识负迁移致误

知识迁移就是一种学习对另一种学习的影响．在学习过程中，任何学习都是在学习者已经具有的知识经验和认知结构、已获得的动作技能、习得的态度等基础上进行的，这种新旧学习之间的影响就是知识迁移．知识的正迁移可以提高学习效率，产生事半功倍的效果．但有些学生往往只注意到新旧知识表面的相似性，而意识不到它们之间内在的本质区别，从而误用了某些知识，导致了错误的出现，这就是知识的负迁移．