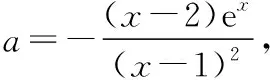函数零点问题的题型归类及解题策略
2018-07-27甘肃张自鹤
甘肃 张自鹤
函数的零点问题,是高中数学中常见的一类问题,纵观近几年的高考试卷可发现,因其考查范围广,考查方式灵活,设计的题目可浅可深,变化多样,对学生思维要求的高低灵活性大,零点问题已越来越频繁地出现在各类试题之中,试题的考查也已由易变难,呈现方式也越来越灵活多样.故有必要对函数的零点问题做一归类研究,以期对教与学有所帮助.归纳起来主要有以下几种类型.
类型一:根据零点存在性定理确定零点的位置
利用函数的零点存在性定理确定零点所在的位置,是零点问题中最常见的一类题型,其要点是要保证函数在某个区间内是连续的,且在这个区间两端点处的函数值为异号.
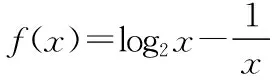
( )
A.(0,1)_____________________B.(1,2)
C.(2,3) D.(3,4)
【分析】本题主要考查函数零点的判定定理的应用,此类题属基础题.
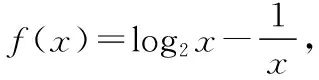
【评注】根据函数零点存在性定理判定零点所在的区间是解决此类问题的基本方法.
【变式训练】已知实数a,b满足2a=3,3b=2,则f(x)=ax+x-b的零点所在的区间是
( )
A.(-2,-1) B.(-1,0)
C.(0,1) D.(1,2)
答案:B
类型二:根据函数解析式求函数的零点
求函数零点的基本方法:一是求方程f(x)=0在定义域内的根,二是求函数图象与x轴的交点的横坐标.

【分析】本题主要考查函数零点的求法,其基本思路就是令函数值为0,进而解方程并在其定义域内取值即可.
【解析】∵当x<0时,g(x)=f(x),
∴g(-2)=f(-2)=-ln3.
令y=g(x)+1=0得g(x)=-1,

【评注】本题考查了分段函数函数值的计算,函数零点的计算,属基础题.
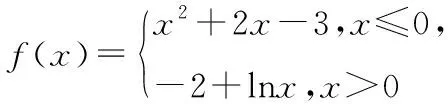
答案:x=-3,x=e2.
类型三:根据函数解析式判断和讨论零点的个数
判断和讨论零点的个数也是常见的一类问题,此类问题常常是与含参数的函数式有关,其常用的解决方法:一是分类讨论,通过研究函数的单调性来研究函数图象的变化趋势,进而借助数形结合思想来解决;二是利用分离参数法进行合理转化,构造新函数,把问题转化为两函数的交点问题来解决,一般是转化为一条直线与一条曲线,通过研究新曲线的变化趋势,然后借助数形结合解决.题目属中等偏难问题.
例3设a为非负实数,函数f(x)=x|x-a|-a.
(Ⅰ)当a=2时,求函数的单调区间;
(Ⅱ)讨论函数f(x)的零点个数,并求出零点.
【分析】(Ⅰ)先讨论去绝对值,写成分段函数,然后分别考虑当x≥2时与当x<2时的单调区间;(Ⅱ)讨论a的正负,利用二次函数的单调性以及函数的极值与0进行比较,再分别判定函数f(x)的零点个数.
【解析】(Ⅰ)当a=2时,
①当x≥2时,f(x)=x2-2x-2,
∴f(x)在(2,+∞)上单调递增;
②当x<2时,f(x)=-x2+2x-2,
∴f(x)在(-∞,1)上单调递增,在(1,2)上单调递减;
故f(x)的单调递增区间是(-∞,1)和(2,+∞),单调递减区间是(1,2).
(Ⅱ)(1)当a=0时,f(x)=x|x|,
函数y=f(x)的零点为x0=0;
(2)当a>0时,
故当x≥a时,f(x)=x2-ax-a,
∴f(x)在(a,+∞)上单调递增,f(a)<0;
当x 由x2-ax-a=0解得f(x)的零点为 ∵f(a)<0,∴函数f(x)与x轴有三个交点, 即有三个零点, ∴函数y=f(x)的零点为 综上可得,当a=0时,函数的零点为0; 当0 当a>4时,函数有三个零点 【评注】求函数零点的基本方法是解方程f(x)=0的根,并在其定义域内取值,有时还需要先利用数形结合来判断根的个数及根的情形,然后再解方程取值. (Ⅱ)讨论函数y=f(x)零点的个数. 此类问题近年来频频出现在高考试卷中,考查题型也已由选择题、填空题逐步过渡为解答题,解决这类问题的基本思路是通过研究函数的单调性,借助数形结合思想来解决;常用方法一是分类讨论法;二是分离参数法. 例4(2017·全国卷Ⅰ理·21)已知函数f(x)=ae2x+(a-2)ex-x. (Ⅰ)讨论f(x)的单调性; (Ⅱ)若f(x)有两个零点,求a的取值范围. 【解析】(Ⅰ)f′(x)=2ae2x+(a-2)ex-1=(aex-1)·(2ex+1)(x∈R). ①当a≤0时,f′(x)=(aex-1)(2ex+1)<0恒成立,故函数f(x)在(-∞,+∞)单调递减. ②当a>0时,由f′(x)=(aex-1)(2ex+1)=0 得x=-lna, 当x∈(-∞,-lna)时,f′(x)<0; 当x∈(-lna,+∞)时,f′(x)>0. 故而可得函数在(-∞,-lna)单调递减, 在(-lna,+∞)单调递增. (Ⅱ)(ⅰ)若a≤0,∵函数f(x)在R上递减, 则f(x)至多有一个零点. (ⅱ)若a>0由(Ⅰ)可知, 故f(x)只有一个零点; 故函数f(x)没有零点; 即极小值小于0, 又f(-2)=ae-4+(a-2)e-2+2>-2e-2+2>0, 故f(x)在(-∞,-lna)有一个零点. 则f(n0)=en0(aen0+a-2)-n0>en0-n0>0. 因此f(x)在(-lna,+∞)有一个零点. 综上可知,a的取值范围为(0,1). 【评注】函数零点问题常常可与相应方程的实根问题相互转化.已知函数f(x)有两个零点求参数取值范围,第一种方法是直接对含参函数进行研究,研究其单调性、极值、最值,注意点是若f(x)有两个零点,且函数先减后增,则只需其最小值小于0,且还需验证在最小值两边存在大于或等于0的点,反之亦然.第二种方法是分离参数法,构造一个不含参数的函数,进而研究新函数的单调性、极值、最值,并判断y=a与其交点的个数,从而求出a的范围. (Ⅰ)求f(x)的单调区间; 证明与零点有关的不等式问题常常是与函数的双零点有关的不等式,其类型主要是与双零点的和,积,商等形式有关的不等式,其常用的解决方法:一是合理转化进行等价变形;二是构造出辅助函数,通过研究该函数的单调性来证明. 例5(2016·全国卷Ⅰ理·21)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点. (Ⅰ)求a的取值范围; (Ⅱ)设x1,x2是f(x)的两个零点,证明:x1+x2<2. 【分析】对(Ⅰ)可继续沿用例4的方法,先求导,进而对参数进行分类讨论,得到函数的单调性,从而得到函数f(x)的大致图象,进而得到f(x)存在两个零点的条件.本题也可通过分离参数法将问题转化为两个函数图象的交点问题来解.对(Ⅱ)可借助第(Ⅰ)问的结论来证明,由于不能求出f(x)的表达式,从而问题的关键是将x1+x2<2的证明转化为证明f(x1)>f(2-x2),进而构造出辅助函数h(x)=f(x)-f(2-x),通过研究h(x)的单调性得到问题的证明. 【解析】(Ⅰ)本例我们用分离参数法来解决. 令f(x)=(x-2)ex+a(x-1)2=0, 当x=1时,f(x)=-e≠0,∴x=1不是f(x)的零点; 可知当x<1时,g′(x)>0,g(x)>0; ∴g(x)在(-∞,1)单调递增; 当x>1时,g′(x)<0,而g(x)∈R; 画出g(x)的简图可得,欲使直线y=a与g(x)的图象有两个交点,则只需a>0即可. 综上可得,a的取值范围为(0,+∞). (Ⅱ)不妨设x1 x1∈(-∞,1),x2∈(1,+∞),2-x2∈(-∞,1), ∵f(x)在(-∞,1)单调递减, 从而将x1+x2<2的证明转化为证明f(x1)>f(2-x2)(x2>1),又f(x1)=f(x2)=0, 从而问题可转化为证明f(x2)>f(2-x2), 证明如下: 令h(x)=f(x)-f(2-x), 代入可得h(x)=(x-2)ex+xe2-x, 则h′(x)=(x-1)(ex-e2-x), ∴当x>1时,h′(x)>0,∴h(x)在(1,+∞)单调递增, 故当x>1时,h(x)>h(1)=0, 从而有f(x)>f(2-x),也即f(x1)>f(2-x2), ∵f(x)在(-∞,1)单调递减,故x1+x2<2. 【评注】对于含有参数的函数的零点问题,通常要根据参数的取值进行分类讨论或分离参数后研究新函数的单调性,进而借助数形结合来解决;而解决函数不等式证明问题的思路则是通过适当转化后,构造出恰当的函数,利用导数研究函数的单调性或极值来破解. 【变式训练】已知函数f(x)=lnx-cx(c∈R). (Ⅰ)讨论函数f(x)的单调性; (Ⅱ)设函数f(x)有两个相异零点x1,x2,求证:x1·x2>e2.



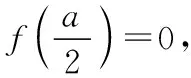
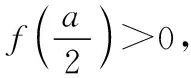


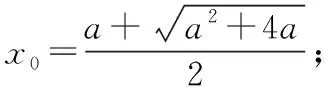




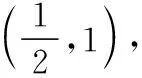
类型四:根据零点个数求参数的取值范围
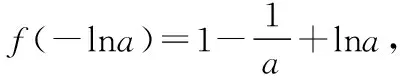




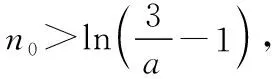




类型五:证明与零点有关的不等式