考虑空间效应的岩堆体隧道管棚力学模型研究

2018-07-24丁祖德刘新峰

铁道学报 2018年7期

丁祖德, 付江，刘新峰, 黄娟

(1. 昆明理工大学建筑工程学院，云南昆明 650500； 2. 中南大学土木工程学院，湖南长沙 410075)

管棚法主要利用管棚钢管和拱架形成的梁拱结构，起到加固围岩、扩散和传递开挖释放荷载的作用，能有效防止围岩坍塌及控制围岩变形，是隧道与地下工程软弱地层及浅埋破碎段施工中广泛采用的一种辅助工法[1-13]。

近年来，对管棚力学机制和力学模型的研究已逐渐得到国内外学者的重视，取得了一些研究成果。归纳起来大体分为数值计算模型和荷载-结构模型，其中数值计算模型采用提高岩土体材料参数模拟管棚作用，或采用梁单元、实体单元直接模拟管棚[1-2,4-6]。前者涉及如何提高材料参数的问题，主观随意性较大；后者涉及岩土体与管棚单元的相互作用问题，计算难度较大。荷载-结构模型由于其受力明确、计算较为简单，应用最为广泛。各学者提出的管棚荷载-结构模型均以弹性地基梁模型为基础，主要差异体现在荷载、地基梁模型和基床系数的选择上[8-11]。董新平等[8]建立管棚空间棚架模型，深入分析了管棚的作用机理。苟德明等[9]建立了弹性固定端双参数Pasternak模型。郑俊杰等[10]阐述常基床系数管棚弹性地基梁模型的缺陷，考虑掌子面前方基床系数的变化，提出了变基床系数管棚力学模型。

现有的荷载-结构模型研究成果为管棚力学机理分析提供了理论依据，并运用于隧道施工参数的优化分析[13]，但也存在一些不足，首先是在荷载的选择上，多采用上覆土重，与实际所受围压压力不符。实际上对于松散介质浅埋隧道[14]，采用太沙基理论可考虑隧道开挖尺寸、埋深以及围岩参数的影响，实践证明用其计算浅埋隧道围岩压力误差较小，比较合理。其次，在进行管棚力学机制分析时，岩土体的基床系数k通常取为常数，文献[10]虽然考虑了变基床系数的影响，但所建的变基床系数分布模型不能考虑隧道掌子面空间效应和围岩应力释放率的影响。基于此，本文结合岩堆体隧道施工实践，建立岩堆体隧道洞口浅埋段的三维有限元模型，分析不同围岩参数及应力释放率条件下掌子面附近基床系数分布规律。在此基础上，采用太沙基理论计算外荷载，建立考虑空间效应的变基床系数管棚力学模型。并与文献[13]的实测结果进行对比，对管棚挠度分布的影响因素进行深入分析。

1 考虑空间效应的基床系数分布规律

由于隧道开挖引起周边围岩应力重分布，改变了掌子面附近的围岩基床系数，而基床系数的改变一方面与岩土体的物理力学性质密切相关，另一方面与围岩开挖的应力释放率、开挖空间效应等因素有关。在此，建立岩堆体隧道洞口段三维有限元模型，研究基床系数k的分布规律。

1.1 计算模型

以云南麻柳湾至昭通高速公路某岩堆体隧道洞口浅埋段为例，计算模型见图1。模型范围取为100 m×100 m×65 m(长×宽×高)，隧道埋深25 m，隧道开挖宽度11.4 m，开挖高度10.33 m，重度γ=20 kN/m3。模型边界取为：顶部自由边界，左右施加水平方向约束，底部施加竖直方向约束。选取围岩弹性模量E、泊松比μ以及围岩应力释放率L等3个因素，每个因素取3个水平进行组合，共计27个计算工况。其中，围岩的弹性模量E取为100、200、400 MPa；泊松比μ取为0.2、0.3、0.4；围岩开挖应力释放率L取为0.6、0.8、1.0。计算模拟各组合参数下的隧道开挖，隧道开挖至2倍洞径时结束(此时可忽略模型边界效应的影响)。

1.2 计算结果及分析

基于弹性理论的圆形隧洞围岩弹性抗力系数计算方法[15]，围岩的基床系数k可表示为

( 1 )

式中：pr为量测位移测点设置后的围岩释放荷载；ps为围岩与支护间的接触压力；ub为量测支护外边界位移；a为隧道半径。

提取27个计算工况隧道掌子面前方拱顶沿线的竖向位移和竖向应力，根据基床系数k的定义，并利用式( 1 )得到的围岩初始基床系数k0，得到各工况拱顶围岩基床系数沿隧道纵向的分布,见图2。

由图2(a)可见，掌子面前方基床系数呈曲线变化，掌子面处基床系数最小，在远离掌子面处基床系数最大，即为初始基床系数值。kmin约为9.38 MPa/m，基床系数最小值与最大值之比约为0.7。基床系数的变化范围约为1.5倍隧道开挖跨度。不同泊松比条件下基床系数变化较明显，随着泊松比的增大，基床系数逐渐减少。由图2(b)可见，在相同的初始基床系数下，应力释放率越高，掌子面处的基床系数衰减越明显，基床系数沿隧道纵向的变化越大。由图2(c)可见，弹性模量越大，其初始基床系数越大，但弹性模量的增大，对基床系数纵向分布的影响较小。

1.3 基床系数纵向分布模型

根据基床系数沿隧道纵向分布特点，基床系数k的拟合函数为

k=a·e-bx+c

( 2 )

式中：a、b、c为拟合参数。

基于多元线性回归，可建立拟合系数a、b的回归方程为

a=-0.029 5E-6.647 0L+16.755 0μ+0.298 3

( 3 )

b=-0.027 5L+0.000 06E+0.847 0μ

( 4 )

假定掌子面处的基床系数kmin与初始基床系数k0关系为

( 5 )

式中：f(E,μ,L)为E、μ、L的多元函数。

根据各工况下的E、μ、L及kmin与k0的比值，可得

f(E,μ,L)=0.335 5L+0.000 3E+1.314 5μ

( 6 )

当x=0时，有

( 7 )

可得

a=k0·[f(E,μ,L)-1]

( 8 )

将式( 8 )代入式( 2 )，可得

k=[f((E,μ,L)-1)·e-b·x+1]·k0

( 9 )

以图2(a)中的3种计算工况为例，依据式( 9 )得到的掌子面前方拱顶围岩基床系数的拟合结果见图3。其最小相关系数R2=0.965，拟合效果好。

2 岩堆体隧道管棚力学模型

2.1 模型的建立

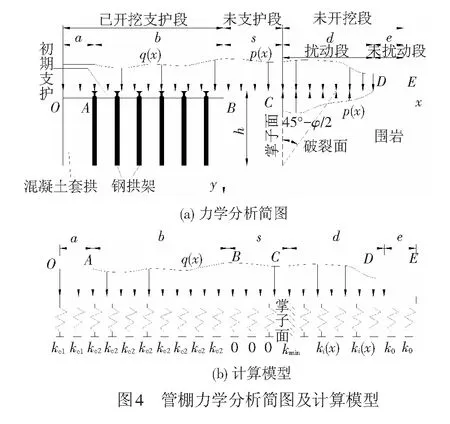
根据已有成果[9-13]，管棚在位于掌子面附近的钢管变形及内力最大，当隧道开挖一个进尺且尚未支护时管棚受力处于最不利状态，可建立单根管棚的力学模型，其受力情况见图4(a)。

对于岩堆体这种松散介质，围岩自承载能力较弱，采用太沙基理论计算围岩压力，实践证明其误差较小，比较合理。而对掌子面前方未开挖段，由于掌子面处围岩的松动变形，围岩变形波及掌子面前方一定范围，在掌子面前方形成松弛区CD段，故该区段内管棚仍受到围岩压力作用。

由图4(a)可见，可将管棚全段划分为5个部分：OA段，管棚设置在混凝土套拱内，管棚的位移及转角较小，受到了较强的约束作用，本文采用具有较大刚度的弹簧来模拟；AB段，开挖并已施做初期支护段，其上作用的围岩压力采用太沙基公式计算，钢管采用Winkler弹性地基梁模拟；BC段，开挖但未施做初期支护段，其上作用的围岩压力仍采用太沙基公式计算，钢管此时不受地基弹簧约束；CD段，未开挖，但受开挖扰动形成的松弛区段，其上作用的围岩压力采用太沙基公式计算，由于受到掌子面围岩约束解除的影响，该段的基床系数采用式( 9 )表示的曲线变化形式；DE段，未开挖且未受施工影响段，基床系数取为常数。由此，可得到考虑空间效应的变基床系数管棚力学分析模型见图4(b)。图中，OA段、AB段分别采用基床系数kc1和kc2，取相同值kc；BC段基床系数取为0；CD段基床系数按式( 9 )取值；DE段取未扰动的初始基床系数。

2.2 计算荷载

对于岩堆体浅埋隧道，可采用太沙基理论计算围岩压力q，其具体表达式为

q=p·δ

(10)

(11)

式中：δ为管棚环向间距；b1为计算宽度，b1=B+h·tan(45°-φ/2)。其中，B为隧道开挖半宽，h为隧道开挖高度；γ为岩体重度；K0为侧向压力系数；H为隧道覆土厚度；c为岩体黏聚力；φ为岩体内摩擦角；q0为地面超载，若有地面荷载时计入。

2.3 管棚挠曲微分方程的求解

把管棚中的钢管等分n段(见图4(a))，每段长度取为l。按照Winkler弹性地基梁理论，有

(12)

式中：pi、Ki、ωi、Ri为第i小段的平均反力、基床系数、挠度、总反力；d0为管棚直径。

这样，将图4(a)中的连续梁变为支撑在n小段弹性支座上的离散梁。考虑CD段基床系数变化时，当分段建立地基梁的挠曲微分方程后，四阶变系数微分方程无法求解，不能获得解析解[10]。本文采用文献[10]的方法，通过编制Matlab程序，运用有限差分方法求其数值解。

依据梁的挠曲微分方程为

(13)

式中：E为梁的弹性模量；I为梁的惯性矩；M为梁的截面弯矩。

二阶导数利用中心差分近似代替，可得

(14)

将式(14)带入式(15)，可得

(15)

将梁在i处切开，对i处端点取矩，根据静力平衡条件有

(16)

式中：Mp,j为j处端点左侧隔离体外荷载对该处端点的弯矩。

结合式(15)和式(16)可得

(17)

式中：i的取值从2～n-1，根据式(17)可以得到相应的n-2个等式。

再结合梁的静力平衡方程

(18)

(19)

由此可得n个方程式并进行联立求解，即可解出简化后的各子段梁的挠度，再利用材料力学公式，可得到管棚的内力。

2.4 算例分析

为了验证模型的有效性，本文提取文献[13]的管棚实测竖向位移值，并与常基床系数下的解析解、本文考虑空间效应变基床系数有限差分法解进行对比，见图5。

由图5可见，由于常规模型没有考虑掌子面附近的空间效应和基床系数的变化效应，从挠度曲线分布形态看，其挠度曲线在掌子面处突然折转，没有平缓过渡段，与实际曲线形态差别较大。当考虑掌子面的情况后，本文模型的曲线形态与实际较为接近，若能较准确的定出上覆压力，则能得到更精确的挠度分布曲线。因此，在进行管棚挠度及内力分析时，需要考虑隧道开挖效应的影响。

3 管棚挠度分布影响参数

为更好地认识管棚变形机制，利用本文所提管棚模型，进行开挖进尺、开挖高度、管棚钢管直径等施工因素，以及基床系数、应力释放率、隧道埋深等地质因素下的管棚变形分布影响参数分析。

以赵家屋岩堆体隧道洞口段管棚支护为例，管棚长30 m，弹性模量为106 GPa，管棚钢管厚度6 mm，管棚间距0.4 m，其他的计算参数见表1。计算时，把管棚钢梁等分成300段，每段梁长为0.1 m。基于已施做初期支护的基床系数kc为恒定值，根据相关资料取kc=90.1 MPa，采用太沙基理论计算管棚上的分布荷载，各段均匀分布。采用Matlab编程，计算出隧道初期支护段、未支护段以及围岩扰动段管棚的挠曲线分布。

表1 计算参数

3.1 隧道开挖进尺分析

不同的套拱及已施做初期支护段长度，管棚受力状态不同。当嵌入已支护段长度过小，管棚受套拱嵌固作用明显；当伸入未开挖段长度过小，则管棚受岩土体约束不足，对于这两类情况，开挖面位置对管棚扰度及受力产生明显影响。为了消除开挖面位置的影响，计算分析时选择较适中位置，统一取隧道已开挖支护段长度为12.5 m。在开挖进尺为0.5、1.0、1.5、2.0、2.5 m 等5种情况下，管棚挠度曲线分布见图6。

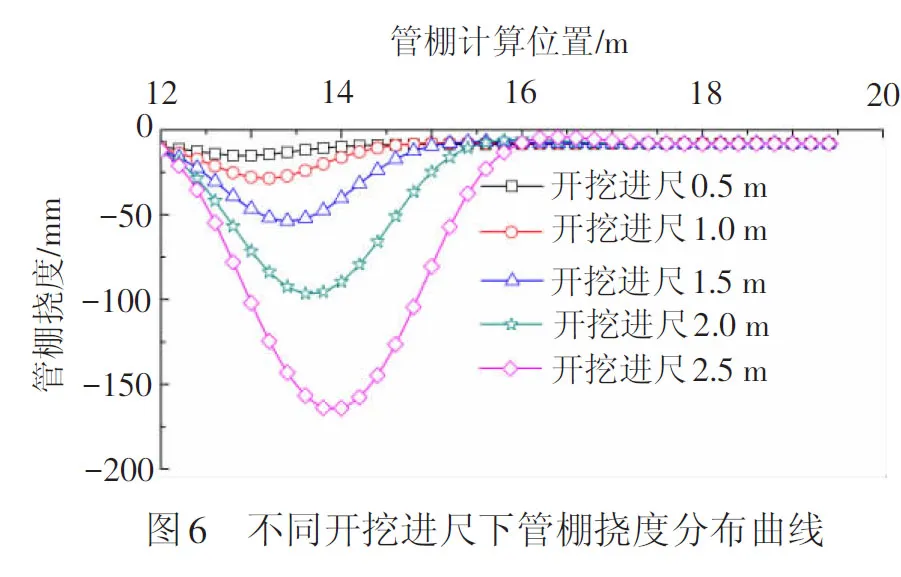
由图6可见，随着开挖进尺的增大，管棚钢管的竖向位移急剧增大，位移最大值位于开挖未支护段。开挖进尺由0.5 m增至2.5 m，竖向位移最大值从15.2 mm增至164.8 mm，增幅超10倍，挠曲线受开挖进尺的影响范围也明显增大。可见，开挖进尺对管棚挠度分布影响显著。以上的结果是按照三台阶法开挖，考虑上台阶开挖情况，开挖高度取3.5 m。在这种情况下，开挖进尺取为1.5 m时，其最大竖向位移在已达53.7 mm，考虑到岩堆体隧道围岩的松散破碎性，建议开挖进尺不超过1.0 m。

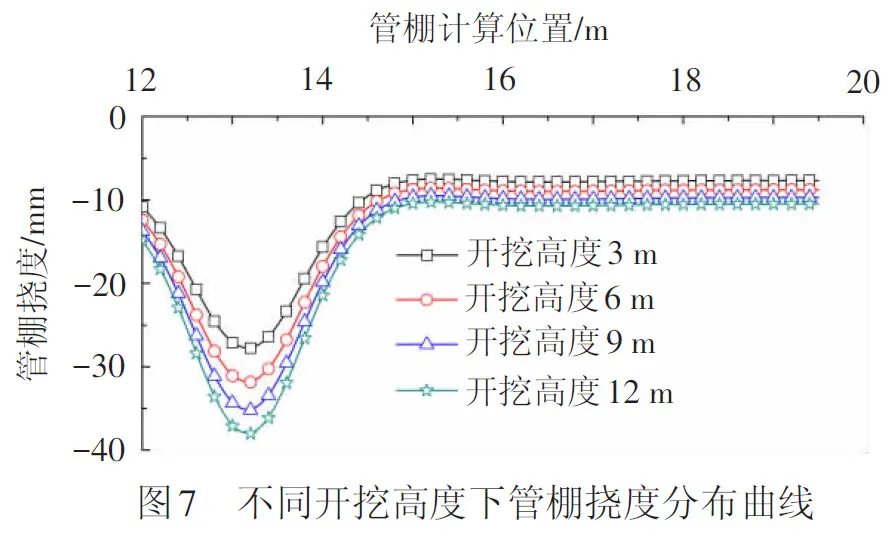
3.2 隧道开挖高度的影响

为简便，以下分析当中隧道的开挖进尺均取1.0 m。管棚和围岩参数不变，通过改变隧道开挖台阶高度，分别考虑3、6、9、12 m等 4种情况。隧道各开挖台阶高度下管棚挠度分布曲线见图7。由图7可见，总体上开挖台阶高度越大，钢管的竖向位移越大，因此，在隧道施工时需合理控制开挖高度。开挖高度在3～12 m变化时，钢管挠度从27.8 mm增大到38.0 mm，增幅36.7%。对于岩堆体隧道，开挖高度取3～6 m之间较合适。

3.3 管棚直径的影响

分别选取管棚直径为108、89、42 mm 等3种截面情况，计算不同直径对管棚钢管的竖向位移分布的影响，见图8。

由图8可见，随着管棚钢管直径的减小，其挠度成比例增加。直径为108 mm时，管棚钢管最大挠度为28.5 mm；直径为89 mm时，增加到42.2 mm；直径为42 mm时，急剧增大到233.8 mm。管棚钢管直径越大，其截面抗弯刚度越大，即抵抗挠度变形的能力越强。总体而言，管棚钢管直径对管棚挠度分布的影响较大。对于岩堆体隧道，建议取108 mm及以上大直径管棚，以增强其整体刚度。

3.4 基床系数的影响

取围岩的基床系数分别为100、200、300、500 MPa/m 4种情况，各工况下管棚钢管挠度分布曲线见图9。由图9可见，基床系数越大，钢管的竖向位移越小，竖向位移分布越集中。基床系数减少，说明围岩状况变差，使得其对钢管的约束作用减小，因此，在同样的荷载作用下，管棚变形变大。可见，对于松散软弱围岩，需进行预支护和预加固措施，以改善围岩条件。

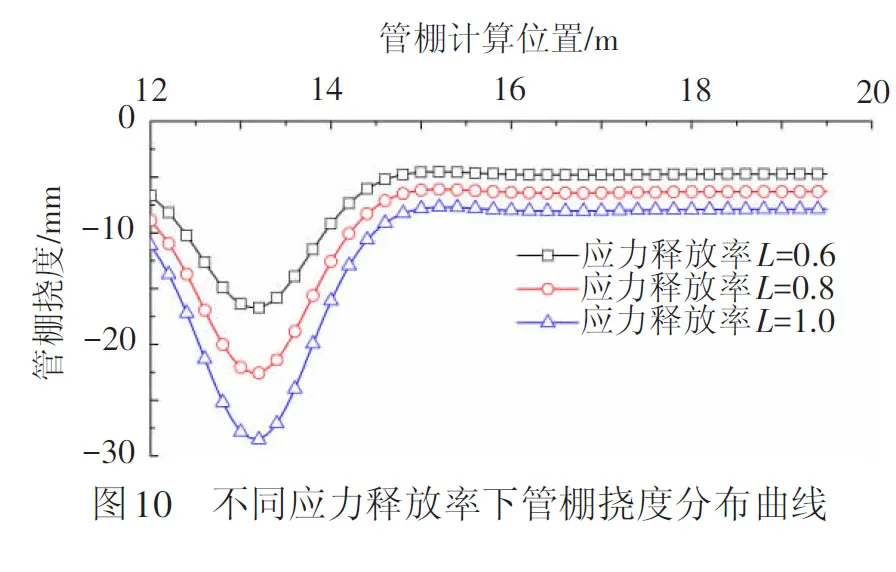
3.5 应力释放率的影响

分别取围岩应力释放率为60%、80%、100%，不同应力释放率下管棚钢管的挠度分布曲线见图10。由图10可见，围岩应力释放率越大，管棚钢管挠度越大，应力释放率从60%增大到100%时，管棚钢管最大挠度增幅1.7倍。

3.6 隧道埋深的影响

取隧道的埋深分别为5、15、25 m等 3种情况，计算各埋深下的管棚钢管挠度分布，见图11。由图11可见，钢管竖向位移随隧道埋深的增加逐渐增大，之后逐渐趋于平稳。当埋深达到某一值后，钢管竖向位移基本不会再随隧道埋深的增加而增大。钢管变形的这种变化规律是由采用太沙基理论计算围岩压力的特点所决定的。从太沙基松散介质理论计算公式(11)可看出，随着隧道埋深的增大，围岩压力变化趋势逐渐放缓直至趋于某一定值，意味着作用在钢管上的荷载增大趋势减弱并趋于稳定，所以钢管竖向位移也表现为上述规律。