Translohr有轨电车导向轮轨接触关系分析
2018-07-24季元进任利惠周劲松
季元进, 任利惠, 周劲松
(同济大学 铁道与城市轨道交通研究院, 上海 201804)
Translohr有轨电车是一种采用中央钢轮钢轨导向的新型胶轮有轨电车系统,其中间的导向装置由2个钢制车轮斜置分布,在预压弹簧的作用下使导向轮的踏面部分与钢轨的两侧接触,从而对车辆进行导向控制(见图1)。导向轮安装时将轮缘部分放置在钢轨的下部,保留一定间隙,不影响车辆正常行驶,且可以有效防止脱轨[1-2]。

上海张江的Translohr有轨电车经过一段时间运行后,导向轮的轮缘出现了明显的磨损,同时在半径25 m曲线上,导向轨的内侧轨腰部位出现严重的侧磨现象[3-4]。文献[3]结合实际线路的磨耗情况,用动力学建模的轮轨简化等效力学模型,分析了不同速度、不同曲线下轮轨的接触状态。但是上述文献的模型对轮轨简化成多点弹簧,预先定义的轮轨接触点并不能反应出实际接触点的位置,更不能反映出轮轨蠕滑状态。为了更真实地研究Translohr有轨电车导向轮轨之间接触状态和磨耗规律,需要对Translohr有轨电车导向轮轨接触关系进行更深入的分析。
目前对于轮轨几何接触的算法主要有2种:轴向切片法和迹线法。迹线法采用数学方法描述轮轨的几何外型,依据空间位置的变化计算接触点,这些点形成一个空间三维曲线,再利用二维方法即可求解[5]。轴向切片法是采用一定间隔的垂直于钢轨截面的平面去切割车轮的外型,计算每个截面下轮轨的法向间隙,寻求所有截面下的最小间距即为此时的轮轨接触点[6]。对于轮轨之间的多点接触问题,Piotrowski等提出了轮轨接触虚拟渗透理论来分析轮轨多点接触问题,并研究了非刚体接触条件下轮轨非椭圆接触斑的方法[7];还提出了条状法,将接触区域划分为多个条状单元,应用Hertz接触理论来计算多点接触时轮轨法向力和切向蠕滑力[8]。舒兴高等开发了一个轮轨2点接触的精确数值解法,由轮轨接触区域的渗透量来确定2点接触的存在条件和影响系数[9]。曾宇清等利用轮对的旋转体特性,推导了轮对在不同投影下底部轮廓的计算公式,给出了轮轨三维接触几何关系的求解方法[10]。任尊松等结合接触迹法,采用轮轨接触距离的一阶和二阶导数来判断发生轮轨多点接触的条件[11]。利用轮对切片投影法计算轮轨接触点时,切片的间距直接影响到计算的精度,杨新文等利用接触范围不断缩小的方法以精确找到接触点[12]。
上述方法讨论的轮轨外型,对于任意横坐标都有惟一确定的纵坐标与其对应,轮轨几何外形之间具有确定的映射关系。对于Translohr有轨电车的导向轮轨,其几何外形在横向和垂向坐标上,并不具有上述一一对应的映射关系,现有方法并不能直接应用以解决这个非映射轮轨关系。
1 轮轨接触几何参数的计算
1.1 轮轨接触求解思路
在轮轨空间几何接触的迹线法和轴向切片投影法中,都是将轮轨作刚性接触处理,考虑车轮和钢轨为刚体,没有弹性。对于传统轮轨系统的车辆,给定轮轨型面,对于每一组横移量y和摇头角α值,对应惟一一组满足刚性接触条件的垂向位移z和侧滚角φ值。自由度z、φ和其他接触参数可通过文献[6]所述的算法进行迭代计算得到,它们都是关于y、α的函数,与y、α具有明确的一一映射关系。因此以自由度y、α为变量,可以创建一个轮轨二维接触数表。
上述迹线法和轴向切片投影法针对传统铁路轮轨关系一般性研究是适用的,但并不适合Translohr有轨电车。Translohr有轨电车的导向轨为倒V形状,一般情况下,左右导向轮的踏面在预压力的作用下与导向轨的2个斜面接触(见图2(a)),当横向力较大时,一侧导向轮的踏面和轮缘会与导向轨上斜面和下斜面接触,另一侧导向轮的踏面与导向轨上斜面接触,呈现出三点接触的状态(见图2(b))。另外,由于车辆的载荷由走行轮胎承受,施加在导向轮上的正压力很小(约800 N),当导向轮受到较大的激扰时可能跳起,即出现导向轮与导向轨不接触的状态(见图2(c)),或者左右导向轮与导向轨2个下斜面同时接触的现象(见图2(d))。
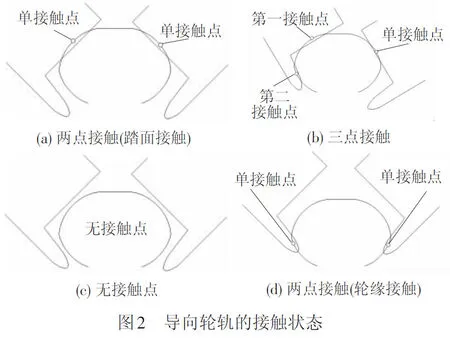
Translohr有轨电车的导向轮相对导向轨存在垂向、横向、侧滚和摇头4个自由度,造成两者之间存在多种多点接触状态。使用假设刚性接触处理这些接触状态是非常困难的。这是因为:假设刚性接触中非独立变量自由度为独立自由度,轮轨之间的接触状态不再总是一种接触状态;即使当4个独立自由度的值确定时,也会在轮轨上形成一个或多个接触区,使用假设刚性接触不能找到某一特定自由度组合下形成的轮轨接触区的位置。
根据Translohr有轨电车导向轮轨的几何外形特点,本文运用轮对切片投影法针对特殊轮轨型面接触求解接触点,通过坐标变换,将导向轮和导向轨非映射的轮轨几何关系转换成为映射关系。针对多点接触问题,本文借鉴轮轨接触渗透量方法,将轮轨接触按照弹性接触方法处理。对于法向力部分的求解采用Hertz理论,而切向部分则参考Kalker简化理论模型,并应用这一方法得到轮轨接触多维度表。
1.2 轮轨接触几何参数计算
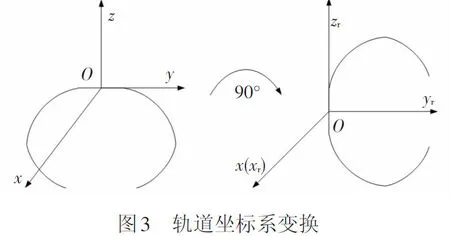
众所周知,钢轨在纵向上的外形轮廓是一样的,类似Translohr的导向轨,在轨道坐标系Oxyz中,部分横坐标y对应2个纵坐标z,不利于后续插值计算接触点的位置。如果将轨道坐标系绕x轴旋转90°,这样就可以把轨道坐标系Oxyz切换到右轨道坐标系Oxryrzr下,此时横向和垂向是一一对应的。
车轮与钢轨定义有所不同,在车轮的坐标系Gwx″y″z″中(图4),作x″=0的平面切割车轮的轮廓,交线即为车轮的主轮廓线。再用平面x″=xi″(i=1,2,…,n)分别切割车轮的外形,于是可以画出n个轮廓外形。
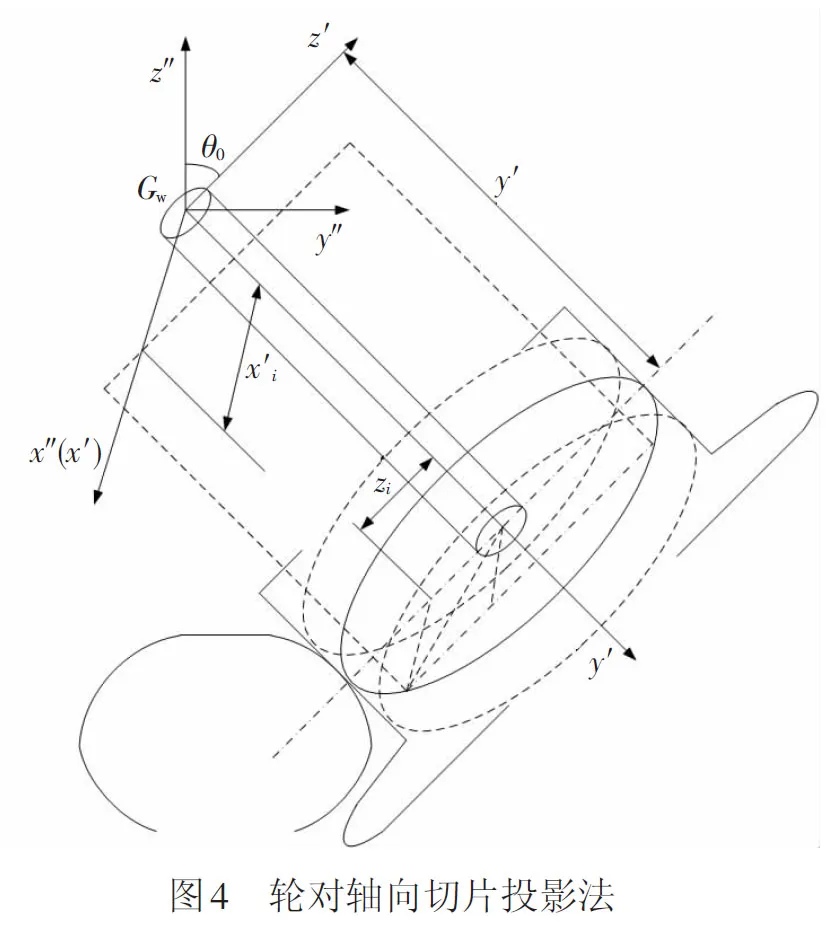
从图4中可以看出,在轮对坐标系Gwx″y″z″中,切割车轮得到的轮廓线在靠近轮缘的位置,横坐标并非只有惟一确定的一个纵坐标和其对应,所以需要引入车轮坐标系Gwx′y′z′,则车轮坐标系与轮对坐标系关系为
( 1 )
由于车轮在轮廓线上任意点的纵坐标可以依据与主轮廓线上横坐标相同的纵坐标求得
( 2 )
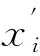
( 3 )
利用轮对轴向切片法计算轮轨接触点时,纵向间距的选择对计算接触参数的影响至关重要。文献[12]研究发现,为平衡计算的精度和计算工作量,在做纵向划分时只需要考虑主轴前后八分之一直径的范围。
2 轮轨力的计算
2.1 轮轨法向力的计算
为求解三维弹性接触问题,可根据上述4个独立自由度值(y,α,z,φ)确定车轮外形与钢轨外形的相对位置。为了描述车轮和钢轨型面,将车轮和钢轨离散成一些点,这些点可以通过样条函数插值得到。通过求解车轮和钢轨间距,确定轮轨可能接触区的位置。在每个可能的接触区,计算出车轮与钢轨之间的法向最大压缩量δ,见图5。
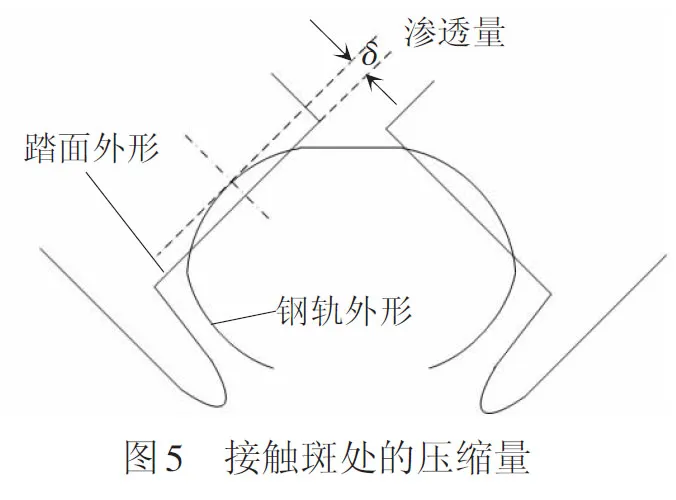
当已知法向最大压缩量δ、接触点处轮轨曲率半径和材料弹性常数后,可利用Hertz接触理论计算出产生此压缩量对应的法向力,法向力和压缩量呈非线性关系,即
( 4 )
式中:P为轮轨法向力;Rwx、Rwy分别为车轮纵向和横向曲率半径;Rrx、Rry分别为钢轨纵向和横向曲率半径;υ1,υ2分别为车轮和钢轨的泊松比;E1、E2分别为车轮和钢轨材料的弹性模量;G为材料剪切模量;m、n、K(e)是椭圆积分有关的参数,可以通过查表得到。
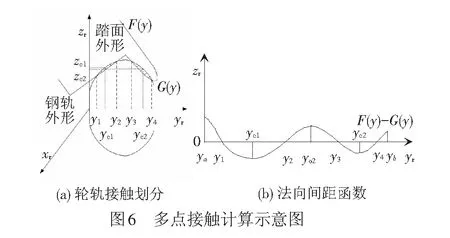
当出现如图6所示的多点接触情况时,以一个x轴向的切片为例,踏面的外形函数为F(y),钢轨的外形函数为G(y),则定义接触点函数C(y)为
C(y)=F(y)-G(y)
( 5 )
求解接触点的个数及区域,接触定义域为[a,b](a、b为钢轨旋转后的左右界限值),因为踏面外形与钢轨外形都是连续函数,则C(y)也是连续函数,对此邻域内任一点y(y≠y0),均有C(y)
2.2 轮轨切向力的计算
2.2.1 轮轨蠕滑率




( 9 )

依据蠕滑率定义得到
(10)

2.2.2 轮轨蠕滑力
轮轨蠕滑力计算参考Kalker快速计算简化理论模型[13-14]。假设接触区中的任一点作用力和该点的弹性位移有关,定义3个柔度系数分别为Lx,Ly和Lz,其中切向力的2个分量可以表示为
(11)
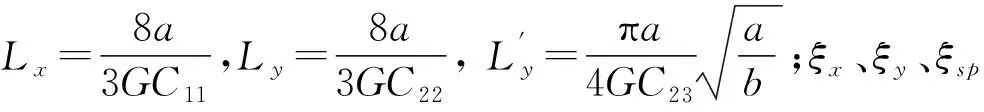
2.2.3 接触数表
三维模型的扫描区域大,如果进行实时数据交互的动力学仿真,则需要耗费大量时间。本文采用的方法是创建一个可供插值的多维数表,通过存在的4个自由度(包括y、α、z和φ)的所有组合计算出四维数表。进行数据插值时,轮对相对于轨道的位置与接触斑处的压缩量有直接对应关系,压缩量可由线性插值得到。而法向力是关于δ3/2的函数,椭圆半轴大小是关于δ1/2的函数,均与δ呈非线性关系,可将其分别转为关于δ3/2和δ1/2的线性关系,有利于提高计算结果的精度。另外,为了更高效的插值计算,减小计算时间,也可以将左右导向轮踏面和轮缘接触做成4个独立的数表,依据轮对的y、α、z和φ,分别得到踏面和轮缘的接触参数值。
3 算例
3.1 Translohr有轨电车的踏面和钢轨廓型
图9给出了Translohr有轨电车的轮轨外型。导向轨外形类似六边形,其轮廓是由一段R100 mm、4段R5 mm、2段R65 mm的圆弧加直线段构成。导向轨总宽度为49 mm,总高度为53.6 mm。导向轮的踏面主要由直线段、R50 mm和R5 mm曲线组成,车轮宽40 mm,轮缘高度为9 mm,轮缘厚度为7 mm。

本文采用基于MATLAB/SIMULINK建立的Translohr有轨电车的动力学模型,整体车辆共计15个刚体,每个刚体具有浮沉、点头、横移、摇头和侧滚5个自由度,共计75个自由度[15]。
3.2 轮轨力计算结果
本文数表的输入是y、α、z和φ,输出是每个车轮上的接触点个数、每个接触区中心点处的坐标、接触角、法向力、接触斑处的压缩量、接触椭圆的大小以及接触斑处的曲率半径。根据参考文献[3]简化模型的结果,轮对的横向位移不超过160 mm。若以轮对质心作为参考坐标,则横向计算范围较大,增加计算量。轮轴的质心高度是500 mm,为了减少计算范围,将轮对参考坐标系移动到钢轨10 mm以上的顶部。此时,轮轴横向位移不超过3 mm,可确定y的范围为-3~3 mm。车辆通过R25 m曲线时,轮对最大摇头角0.14 rad,确定α范围为-0.15~ 0.15 rad。轮对最大侧滚角为0.32 rad,确定φ的范围为-0.4~0.4 rad。最大垂直位移小于1 mm,确定z的范围从0~1 m。4自由度的组合数目为60×30×10×80。
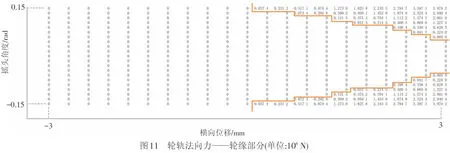
按照上述流程创建Translohr导向轮轨的接触状态和轮轨力数表。图10~图12给出了垂向位移为3 mm,侧滚角为-0.15 rad,横向位移为-3~3 mm,摇头角度为-0.15~0.15 rad时接触状态和轮轨力的计算结果。图10是左侧车轮接触状态数表,表中0代表没有接触点,1代表存在1个接触点,2代表存在2个接触点。图11是左侧轮缘部分轮轨法向力数表,可看出处于对应表1中2个接触点的位置时,才会存在轮缘部分接触。其他情况下,轮缘部分的轮轨法向力为零。图12为左侧踏面部分轮轨法向力数表,可看出对应图10中存在接触点时,就有踏面部分接触;没有接触点时,踏面部分的轮轨法向力为零。
3.3 轮轨力计算结果的应用
将上述轮轨力的计算结果代入到参考文献[3]的动力学仿真模型,仿真分析车辆曲线通过性能。
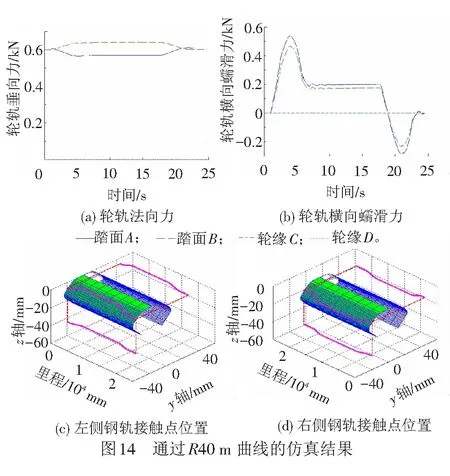
图13给出了车辆通过R25 m曲线的仿真结果(车速20 km/h)。从图中看出:在出缓和曲线段时,内侧导向轮在踏面、轮缘、钢轨之间都存在接触力,说明出现同时接触状态,而外侧导向轮仅仅只在踏面部分存在接触力,说明处于踏面接触状态。仿真得到的轮轨接触状态与实际线路R25 m曲线处观察到的磨耗现象是一致的。
图14给出了车辆通过R40 m曲线的仿真结果(车速30 km/h),从图中看出,2个导向轮都只是在踏面部分存在接触力,说明处于踏面接触状态,此时不会出现侧磨现象。仿真得到的轮轨接触状态与实际线路R40 m曲线处观察到的磨耗现象是一致的。


4 结论
针对Translohr有轨电车的导向轮轨在横向和垂向坐标上并非一一映射的特殊关系,提出求解非映射轮轨力的计算方法。首先通过坐标变换,将导向轮和导向轨非映射的轮轨几何关系转换成为映射关系,然后采用弹性轮轨接触的渗透量法求解导向轮和导向轨多点接触问题。为了便于动力学仿真,建立了Translohr有轨电车的导向轮和导向轨的多维度接触状态表格。应用上述方法得到导向轮和导向轨的多维度接触状态表格,仿真计算车辆在不同半径曲线上的轮轨接触状态。得到结果显示轮轨接触状态与实际观察到的磨耗规律是一致的。
本文提出的非映射轮轨力计算方法能够解决Translohr有轨电车导向轮轨三维多点接触问题,该方法同样可扩展到其他复杂外形非映射关系下的轮轨关系求解问题。