片间短路时变压器铁芯涡流场的三维建模与分析

周利军， 刘桓成， 高仕斌， 江俊飞， 王东阳， 张讥培

(1. 国家轨道交通电气化与自动化工程技术研究中心， 四川 成都 610031；2. 西南交通大学 电气工程学院， 四川 成都 610031)

高速铁路在我国进入快速发展时期，牵引变压器作为牵引供电系统中的核心设备，其安全运行与否直接关系到整个供电系统的运行状态[1]。根据对110 kV及以上等级的变压器事故统计分析发现，由绝缘故障导致的变压器事故占总事故的50%以上[2]，其中片间短路故障就是铁芯故障中一种典型的绝缘故障。铁芯发生片间短路时，在主磁通的感应下短路的硅钢片间形成故障环流，进而导致铁芯空载损耗的增加。严重时，故障区域进一步扩大，所产生的热量会破坏铁芯及绕组绝缘，甚至融化叠片，烧毁铁芯。

针对这些问题，国内外学者对电机和变压器铁芯的片间短路故障展开一系列研究。研究主要围绕故障诊断和理论分析两个方面。在故障诊断方面，目前用于设备检测中的诊断方法主要有:(1)红外摄像机诊断法[3];(2)ELCID测试法[4];(3)FIP探针测试法[5-7]。其中FIP探针测试法由于对功率的要求较低以及容易操作等优势成为目前主流诊断手段。

在故障计算、仿真及分析方面，目前场路分析法和有限元分析法都取得了一定的进展。场路分析法主要利用等效电路对故障时硅钢片的涡流损耗进行定量计算，在整体涡流损耗的计算上经过实验验证具有很高的精确度，但这种方法无法得到故障时铁芯局部涡流场的变化，不能实现局部优化。文献[8-10]建立了由硅钢片叠积而成铁芯的等效电路来预测其磁场和电场特性，并没有提出故障时的计算方法。文献[11]提出了片间短路故障时的等效电路计算方法，并通过实验对不同短路片数和不同频率下涡流损耗的计算结果进行验证，显示了很好的准确性。在有限元分析方面，文献[12]用有限元软件仿真了短路硅钢片内的涡流分布，并分析了其分布的不均匀程度。尽管不能直接模拟电机及变压器等设备故障时的铁芯状态，但这种将有限元分析应用于片间故障分析中的方法为接下来的研究提供了基础。文献[13-15]提出叠片铁芯的等效电导率，这种均质化思想为研究铁磁材料的涡流场提供了一种新的思路。文献[16]基于均质化思想建立了电机定子有限元连续体模型对片间短路故障进行模拟，并与叠片模型下获得的仿真结果进行对比分析，2种模型计算结果相近。有限元分析法可以得到故障时铁芯局部磁通以及涡流的分布，更为直观地反应故障区域涡流场的变化情况，从而为进一步优化设计提供依据。目前的二维模型要求铁芯叠压方向叠片的尺寸一致，对于电机定子铁芯可以满足要求。但变压器铁芯每级叠片的尺寸不同，二维模型将不再适用，因此对三维有限元模型的研究就显得十分必要。

在三维建模时，故障区域处的等效电导率决定了故障涡流的大小和方向，进而会影响到磁通以及涡流损耗的分布，因此本文在考虑实际工况下片间短路故障发展机理的基础上，首先提出短路故障点的等效电导率，并根据牵引变压器建立了故障时的三维有限元模型。其次利用该三维故障模型仿真计算了片间短路时变压器铁芯内部的磁通分布、涡流密度以及涡流损耗，并分析其影响。最后为验证模型的正确性，采用了精确度较高的等效电路法对涡流损耗的计算结果进行验证。结果表明，本文提出的变压器故障模型仿真结果与等效电路计算结果相近，可以满足实际的精度要求，对铁芯局部涡流分布的仿真也可作为优化设计的参考。

1 故障变压器的三维涡流场建模

1.1 铁芯故障点的等效电导率

变压器空载或负载运行时，由原边绕组产生的主磁通沿硅钢片轧制方向在铁芯柱和铁轭中流动。由于硅钢片表面绝缘层的存在，在每片硅钢片中都感应出独立的涡流，见图1。这种涡流在片内电阻中所产生的损耗就是涡流损耗。

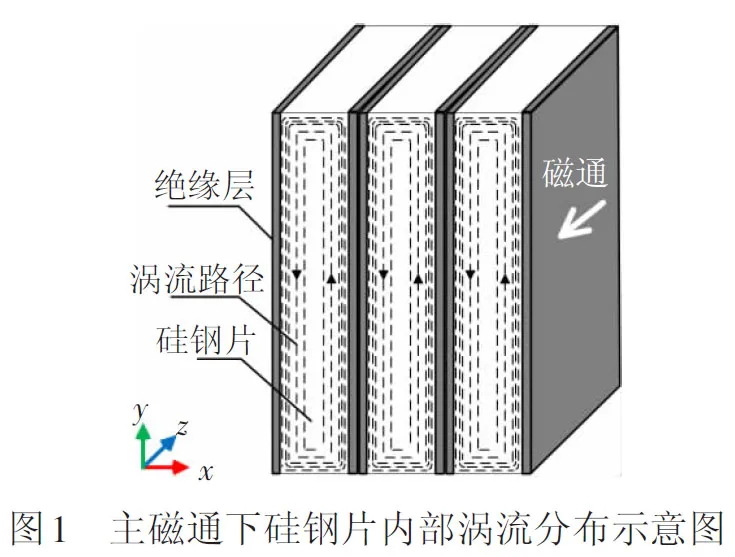
正常情况下，硅钢片厚度很小，且与典型的集肤深度相比太小[17]，可以近似地认为每片硅钢片内部的涡流均匀分布，单位涡流损耗很小。当发生片间短路故障时，主磁通在故障区域硅钢片中感应的涡流受集肤效应的影响，在短路故障点和故障区域边缘处集中分布(见图2)，故障点之间硅钢片的单位涡流损耗急剧增长。该涡流损耗值主要受主磁通密度、频率和短路片数的影响[11]。

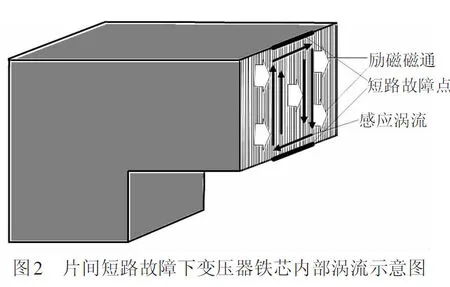
考虑到实际工况，片间短路故障点主要是毛刺等破坏了硅钢片两侧的绝缘形成的，使得在每片中的感应涡流通过故障点相互影响，形成统一的故障环流路径。但除故障点之外，故障区域硅钢片之间的绝缘层仍然存在，每片硅钢片的电磁特性和非故障区域相比保持不变，它们之间的电气联系只通过之间的短路故障点来实现。目前大多数研究直接假设整个故障区域的电导率不同于非故障区域的电导率，这种假设会导致涡流密度和涡流损耗的仿真结果相对实际情况偏大。为进一步消除误差，使仿真结果更接近于工况，应当只对故障点的电导率进行修正，即假设故障点的电导率为各项同性的电导率，并用硅钢片本身电导率σ来表示(根据均质化理论，非故障区域应采用各向异性电导率表述)，其他部分电导率应与非故障区域电导率相同。

1.2 牵引变压器涡流场的三维有限元建模

变压器铁芯由成千上万片高磁导率的硅钢片叠积或卷制而成。而硅钢片之间由于片间绝缘层的存在使得每片硅钢片内的磁通分布和产生的涡流都隔离开来，所以当用有限元方法仿真铁芯叠片时如果对每片硅钢片都加以细致的剖分，工作量将会十分巨大，而且很可能影响到最终的仿真结果，这是不现实的，因此本文建立的变压器故障模型的铁芯应用均质化理论进行等效。

文献[15]提出基于有限元方法的三维方案，其中假设在不发生铁芯故障的前提下，垂直于叠片平面方向的电导率为0，平行于叠片平面方向的电导率简化为Fσ，这样均质化整体的各向异性等效电导率可以表示为

( 1 )

式中：σ为硅钢片本体电导率。本文所采用的变压器模型铁芯的叠装系数为F=0.97，所用硅钢片的电导率σ=2 083 333 S/m，因此非故障点区域均质化模型的等效电导率由式( 1 )计算可得

σy=σz=2 020 833 S/mσx=0 S/m

( 2 )

式中：σx为垂直于叠片方向的电导率;σy、σz分别为平行于叠片平面两正交方向的电导率，具体方向示意见图1。

为更加接近实际工况，本文在均质化变压器模型的铁轭处设置短路故障点，并在故障点处采用本文提出的故障点各向同性等效电导率与非故障点区域加以区分，即设置为σ=2 083 333 S/m。

现以一台QYD-31500/220牵引变压器作为分析的模型变压器，应用ANSYS Maxwell建立三维故障变压器计算模型，见图3。在铁芯铁轭处发生贯穿性的片间短路故障，在铁轭的上下表面各有1个故障点，2个故障点之间的区域为故障区域。

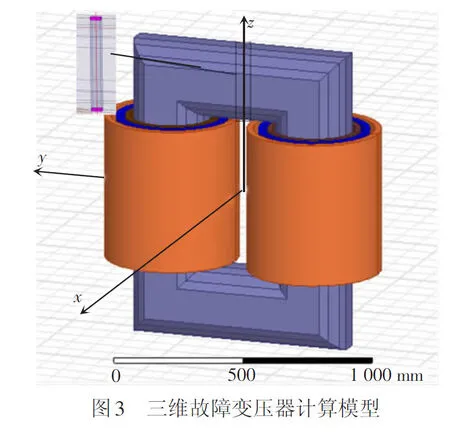
ANSYS Maxwell在进行有限元分析时，对模型采用的是四面体剖分，使用T,φ-φ方程进行求解，大大提高仿真结果的准确性。

2 典型故障工况的有限元仿真

利用1.2节中建立的变压器均质化故障模型对短路片数50片、主磁通密度1.7 T的故障工况进行仿真模拟。为模拟空载实验，得到故障时的铁芯损耗，在高压绕组中施加励磁电流，T、F绕组空载，使铁芯中产生约1.7 T的磁通，见图4。

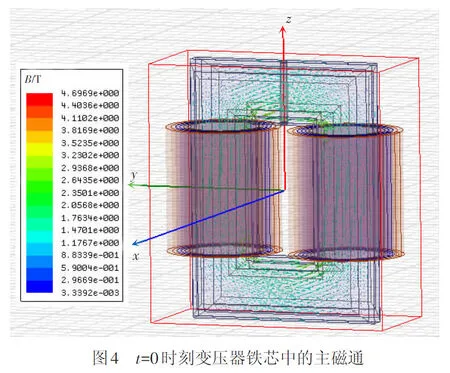
2.1 磁通分布仿真

变压器正常运行时，铁芯内部的磁通密度除在拐角处会激增之外，在铁芯柱和铁轭中基本是均匀分布的。当发生片间短路故障时，由于在短路硅钢片之间产生故障环流，磁通也会发生畸变，见图5。

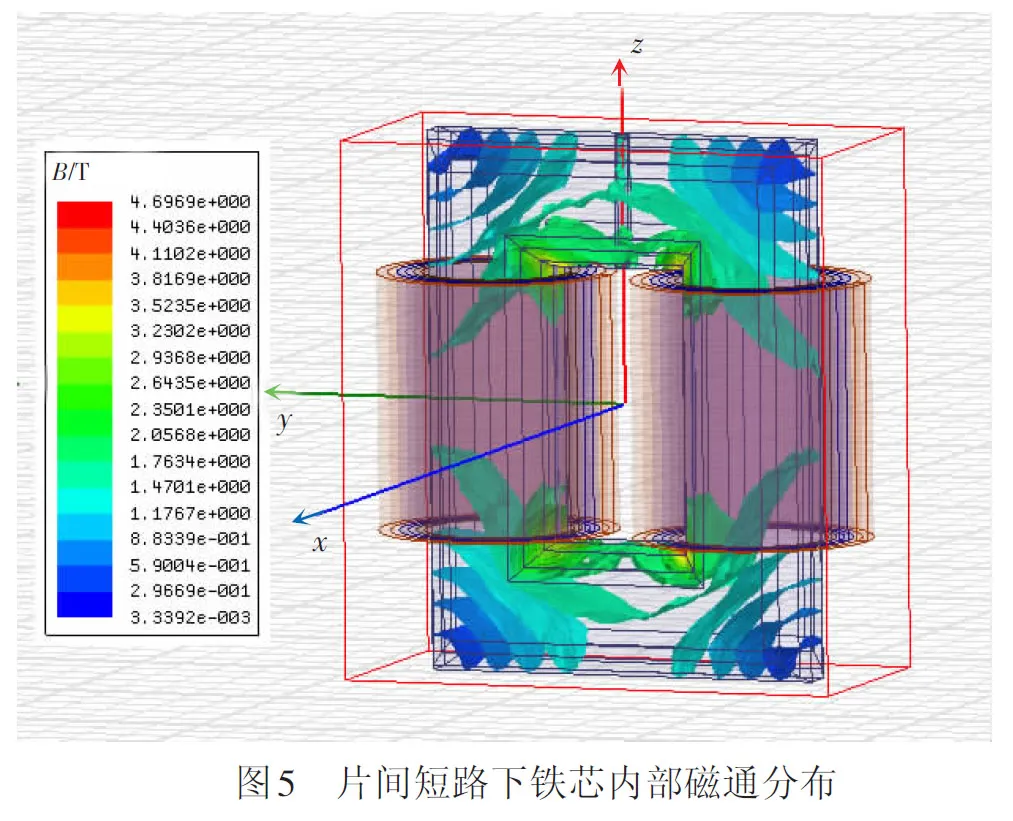
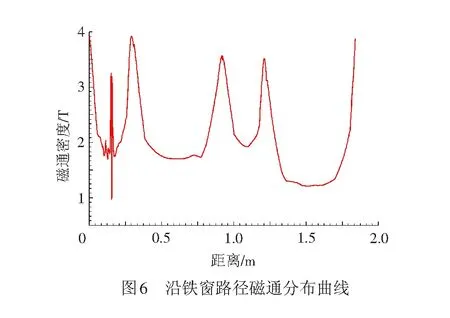
图6是沿铁窗路径磁通密度分布曲线图。由图中可以直观地看出故障点处磁通密度从1.7 T左右畸变为3.3 T左右，增长约1.94倍。

2.2 涡流密度仿真

当发生片间短路故障时，故障区域处的涡流会急剧增大，其密度可达105数量级，见图7。

故障区域和故障点处构成故障涡流的环流路径，见图8，该环流会由于集肤效应的影响集中于故障区域的边缘处。

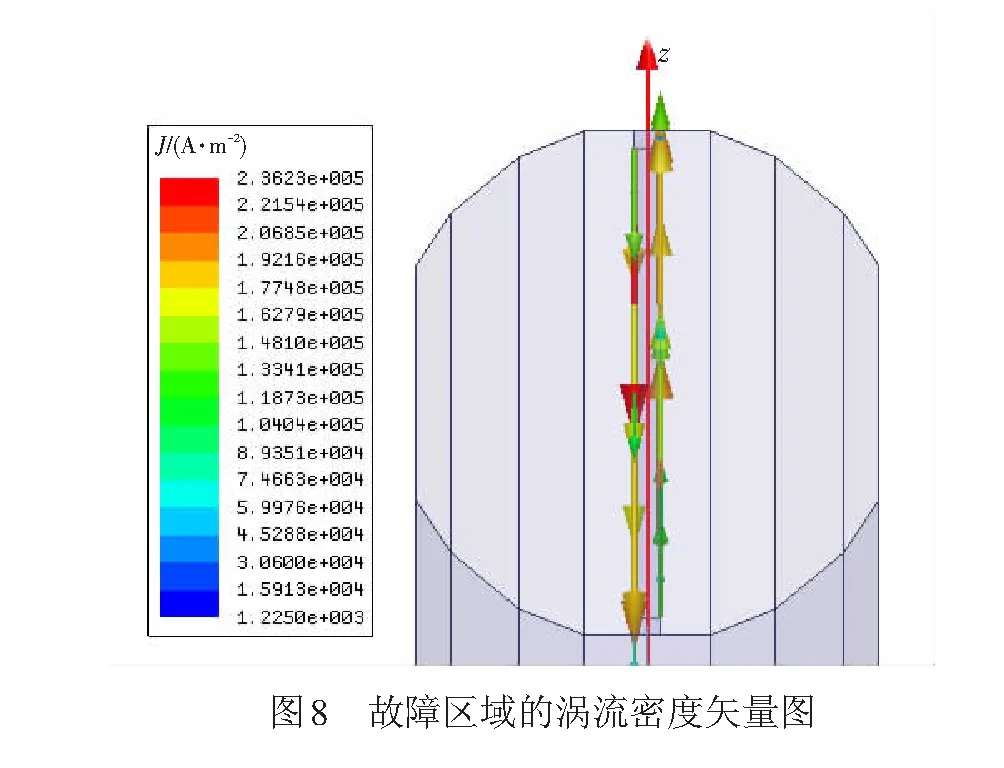
图9是沿铁窗路径上涡流密度幅值曲线图。由图中可看出，故障点处存在明显的涡流效应，并可以注意到故障区域以外的部分其涡流密度幅值均接近于0。

变压器铁轭故障区域的电流密度比其他区域要高很多。由于故障横截面积随着故障区域热量增长而变大，这就使得故障电阻减小，这样感应阻抗变成了惟一限制故障电流的因素[18]。对于实际工程问题，出现这样的现象是很合理的。

2.3 涡流损耗仿真

在对涡流密度仿真的基础上，利用故障模型对涡流损耗在铁芯的分布做进一步的有限元仿真研究，见图10。

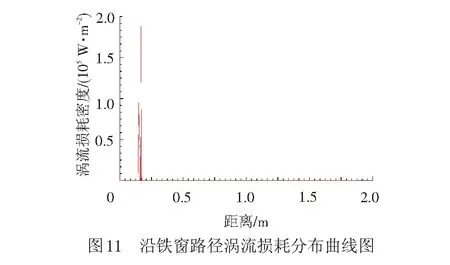
由图11可以更直观地看出，涡流损耗主要分布在故障区域内，其密度也达到了104数量级，非故障区域内的涡流密度接近于0。叠片的厚度和铁磁材料的电阻率是决定涡流密度下限的主要因素，所以片间短路故障对涡流损耗的影响主要是通过改变故障区域的等效叠片厚度和等效电导率来体现的。

3 对比分析及验证

为验证所建模型的有效性和计算结果的正确性，本文搭建了基于P-Spice的故障区域等效电路模型对以上仿真中涡流损耗的计算结果(故障区域具体的涡流损耗值可由Maxwell后处理得到)进行验证，这种等效电路法计算结果的准确性在文献[11]中得到了实验的验证。

3.1 沿涡流路径的等效电路

受集肤效应的影响，交变磁场会在垂直磁通的方向形成一个集中分布于硅钢片边缘附近的环形涡流路径，由于涡流损耗主要和片内的电阻有关，因此沿涡流路径可以根据基本的电路原理等效成一个简单的纯电阻电路[8]。

以一片硅钢片为例，沿涡流路径，硅钢片的4个边都可以用电阻来等效，见图12。

图12中:a为单片硅钢片厚度的一半；x为从涡流路径外边缘到硅钢片中心线的距离；w为单片硅钢片高度；h为单片硅钢片长度；dx为所取涡流在硅钢片厚度x方向的积分微元；dy为所取涡流在硅钢片厚度y方向的积分微元；B(t)为沿z方向的交变磁通，ie为单片硅钢片内的涡流；emf为涡流路径上的感应电动势；rx与ry分别代表沿涡流路径硅钢片在x及y方向的电阻。

( 3 )

式中：ρ为硅钢片电阻率；l对应沿涡流路径硅钢片高度；S为涡流路径在xz平面的截面积。

由于硅钢片的厚度只有0.3 mm左右，因此rx的大小相对于ry来说可以忽略。考虑50 Hz下的集肤深度会大于片厚，可以忽略，这里取dx=a/2。

根据法拉第电磁感应定律，涡流路径上的感应电动势为

( 4 )

式中：B为平行通过硅钢片的磁通密度；A为涡流路径在xy平面所包围的面积，此处A=2xw。因此感应电动势的有效值erms为

( 5 )

式中：f为频率，此处为50 Hz；Bs为磁通密度有效值。

最终可得低频下涡流损耗Pe的计算式为

( 6)

当发生片间短路故障时，硅钢片间的绝缘被短路，绝缘电阻被故障点的接触电阻所代替，片内涡流相互影响。此时的等效电路见图13。图中:rcon为片间短路点的接触电阻。

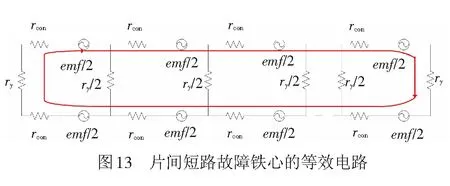
模型材料设置为日本新日铁公司出产的型号为35Z145的硅钢片，其参数见表1。

表1 硅钢片参数表

根据表1中参数可计算得emf=32.86 mV，ry=30.93 mΩ。故障点的接触电阻根据经验值取rcon=5.19 mΩ[19]。

3.2 计算结果验证

考虑变压器实际运行，采用工频50 Hz工况进行分析。根据涡流损耗计算公式，除受频率影响外，涡流损耗还主要与磁通密度和所短路的硅钢片数有关。

将磁通密度设定在1.7 T，应用等效电路法和Maxwell后处理分别对5片，10片，20片，30片以及50片硅钢片发生片间短路时铁芯的涡流损耗进行仿真计算，并与正常工况下的铁芯涡流损耗进行对比，计算结果见表2。

表2 不同片数下铁芯故障区域的涡流损耗 W

由计算结果可以看出，在磁通密度一定的情况下，当发生片间短路故障时，故障区域铁芯的涡流损耗会急剧增大，约为正常工况下的20～30倍。并且随着铁芯短路片数的增加，涡流损耗基本呈线性增加，见图14。

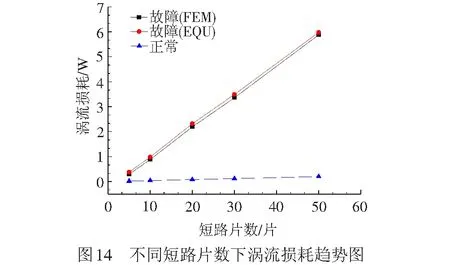
经过误差分析得到，利用有限元模型计算的涡流损耗和等效电路法的计算结果基本吻合，平均相对误差仅为5%左右。并可以注意到随着短路片数的增加，相对误差越小，有限元模型的计算结果越接近于准确值。

将短路片数设定在50片，分别计算在主磁通密度1.2，1.3，1.4，1.5，1.6，1.7 T下的铁芯涡流损耗，计算结果见表3。

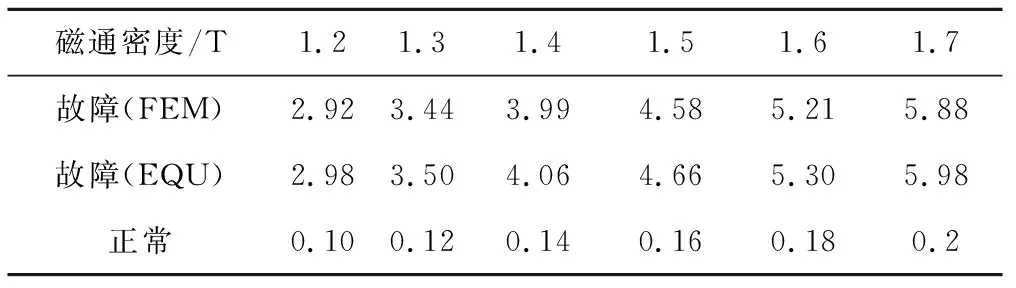
表3 不同磁通密度下的涡流损耗 W

由计算结果可以看出，在短路片数一定的情况下，随着主磁通密度的增加，故障区域的涡流损耗基本呈抛物线趋势增大，见图15。

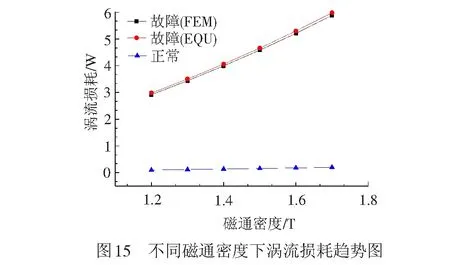
经过误差分析得到，利用有限元模型计算的涡流损耗与等效电路法计算的涡流损耗结果相对误差在2%以下。并可以注意到随着磁通密度的增加，相对误差越小，有限元模型的计算结果越接近于准确值。

由以上分析可知，利用本文提出的有限元均质化故障模型进行后处理计算得到的涡流损耗值与等效电路法的计算结果大致相同，也进一步证实了计算方法的准确性，说明本文建立的三维有限元变压器故障模型对片间短路故障的计算与仿真可以作为实际工况的参考。

4 结论

(1) 在提出变压器铁芯故障点等效电导率的基础上建立了故障变压器三维有限元模型。经过验证可知，涡流损耗的仿真结果与等效电路法的计算结果误差不超过5%，说明本文建立的故障变压器三维模型用于片间短路故障的仿真计算具有较高的精度，其仿真结果可以作为实际工况的参考。

(2) 建立的故障变压器三维有限元模型可以直观地反应发生片间短路故障时铁芯局部涡流场的变化，从而为局部上的优化提供相应的仿真支撑。通过仿真分析可知，发生短路故障时，在铁芯故障区域处的磁通密度、涡流密度以及涡流损耗都会出现激增现象。其中磁通密度比正常情况下增大一倍左右，整体上的涡流损耗会增大20～30倍。