高速铁路单列车动态定价与票额分配综合优化研究

宋文波， 赵 鹏， 李 博

(北京交通大学 交通运输学院， 北京 100044)

随着高速铁路市场化运营的发展，高速铁路收益问题越来越受到铁路管理部门的重视，如何在既有固定的运输能力下提高收益是重要的决策问题。高速铁路旅客运输存在产品易逝性、预售期有限、固定成本高、边际成本低等特点，适合利用收益管理的理论来提高收益。动态定价和票额分配是高速铁路实施收益管理的重要手段，对提高高速铁路收益具有重要作用。目前国家发改委已经发布了《关于改革完善高铁动车组旅客票价政策的通知》，逐步将高铁票价制定权下放给中国铁路总公司，在此背景下研究高速铁路的动态定价和票额分配具有重要的理论价值和实际意义。准确的需求预测是实施动态定价和票额分配的关键，然而需求具有随机性和时变性，很难准确预测，因此，如何在不确定需求条件下进行动态定价和票额分配是本文所要研究的问题。

收益管理起源于20世纪70年代美国航空业，并得到了广泛应用，美国、法国、德国等铁路公司采用收益管理，取得了显著成效。对于收益管理问题，国内外的学者已经做了深入的研究[1-16]。动态定价方面，文献[1-2]运用强度控制理论研究了连续时间的单一易逝品动态定价问题，并将其扩展到多产品动态定价问题。文献[3]研究了顾客到达为非齐次泊松过程下的动态定价问题。文献[4]在需求是价格的线性函数的条件下，利用最优控制理论研究收益管理系统的动态定价问题。文献[1-4]研究中，价格随时间的变化是连续的，然而现实生活中价格的改变是有限的。因此，文献[5-6]研究了离散价格集的连续时间动态定价问题。文献[7-8]对我国铁路利用动态票价进行了理论探讨。文献[9-11]研究了需求不确定条件下的易逝品的鲁棒动态定价模型。以上对于动态定价的研究主要以理论研究为主，并且集中在一般易逝性产品和集装箱班轮运输，在高速铁路旅客运输领域研究较少。票额分配方面，文献[12]研究了铁路收益管理非嵌套席位控制问题，给出了确定线性规划模型和随机非线性规划模型和求解算法。文献[13]研究了两等级票价的席位控制问题，并设计了粒子群智能算法对问题进行快速求解。文献[14-15]研究了我国铁路随机需求条件下的单列车票额分配方法和嵌套式票额分配方法。文献[16]以人公里数最大为目标，通过构建基于客车开行方案的换乘网络来进行票额分配。但是，既有的对高速铁路收益管理的研究中，主要集中在对票额分配的研究[12-16]，通常不考虑价格对需求的影响，然而价格对需求具有调节作用。在进行票额分配时，文献[12-16]通常假设各OD间的需求服从某种分布函数，这样得到的优化方案很大程度上取决于需求分布估计的准确性，一旦需求估计出现偏差，得到的方案可能达不到收益最大化的目的。高速铁路客票动态定价方面的研究才刚起步，目前主要处于理论探索阶段，且一般将其与票额分配独立开来进行研究。然而在实际工作中高速铁路动态定价与票额分配是一个相互联系不可分割的整体，票价的改变会对需求产生影响，从而影响票额分配。

根据对既有研究情况的分析，本文针对需求的不确定性以及目前票额分配模型不能满足需求波动的问题，以收益最大化为目标，建立高速铁路动态定价与票额分配稳健优化模型，并运用稳健优化方法求解，根据客票预售期内每个时间段每个OD客流需求的特点，为其制定价格并分配相应的票额。最后通过具体的案例来验证模型的准确性。所建的模型能够适应需求在一定范围内的波动，防止实际需求与票额分配时的需求相差较大，使得产生的票额分配方案不可行，给现场带来大量的票额调整工作。

1 模型构建

1.1 问题分析

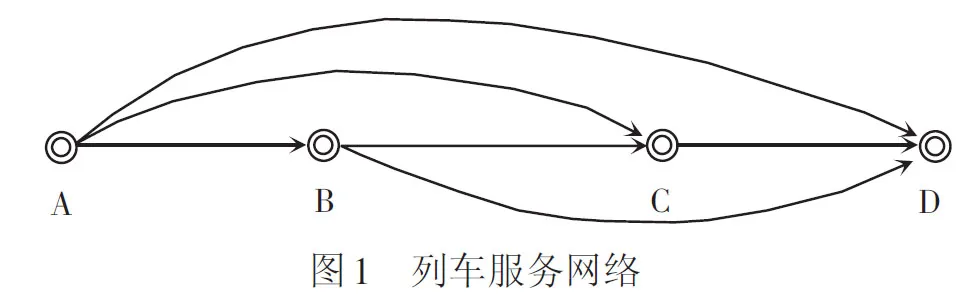
高速铁路列车开行方案规定了列车的运行区段、种类及开行对数。列车的开行方案确定之后，其停站方案也随之确定。列车的停站方案构成了一个具有多区段、多OD的列车服务网络。图1所示为一列车的服务网络，A为始发站，D为终到站，B、C为列车的中间停靠站，则此列车服务于AB、BC、CD 3个区段，承担AB、BC、CD、AC、AD、BD这6个OD间的客流。票额分配的目的是根据客流特点将列车的运输能力分配到这6个OD上，使获得的收益最大。在不考虑超员的情况下，列车在每个区段上的最大运输能力就是列车的定员。本文研究的问题就是将客票的预售过程分为T个时期，根据每个时期t(t=1,2,…,T)内各OD间客流与票价的关系，为各OD制定价格，并为各OD分配相应的票额。本文不考虑运行线路上列车之间的相互影响和列车超员。

1.2 数学模型

xijt表示第t时段OD对(i,j)的票额需求，该需求是不确定的，但是它随价格变化的模式是可以预测的，其为价格pijt的函数，xijt=xijt(pijt)。根据文献[9]，假设随机需求的形式为线性函数和随机误差组合而成，即

xijt=αijt-βijt·pijt+εijtt=1,2,…,T

( 1 )

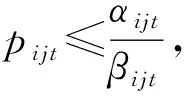
在既有固定的运输能力下，需求不确定条件下的高速铁路动态定价与票额分配综合优化模型(M1)为

( 2 )

s.t.

∀t,∀(i,j)∈FL=1,2,…,m-1

( 3 )

( 4 )

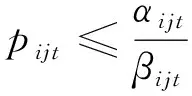
( 5 )

若lek>lij，则

pekt>pijt∀t,∀(e,k),(i,j)∈F

( 6 )

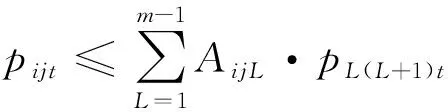
( 7 )

若Ω={L|(i,j)∈F且AijL=1}，则

∀t,∀g∈Ω

( 8 )

pijt∈N

( 9 )

式中：(e,k)为从i站到j站的OD对；Ω为组成OD对(i,j)的各区段集合；N为非负整数集。

式( 2 )是模型的目标函数，通过确定所有OD在预售期内的每个时段的票价和相应的票额，使得铁路运输收益最大。式( 3 )是能力约束，所有OD对(i,j)在任一区段上累积的票额需求之和不得超过列车在该区段的最大运输能力。式( 4 )表示预售期内每个时段各OD的票价不得低于一个票价下限，防止铁路票价过低造成收益损失，同时考虑到铁路运输的社会公益服务特性，票价不能高于一个票价上限，防止运输能力紧张时期(如春节、五一等)票价过高，造成社会不良影响。式( 5 )表示每个时段票额需求不能为负数。式( 6 )表示在预售期的同一时间段内OD距离越长，票价越高。式( 7 )表示在预售期的同一时间段内票价率是递远递减的，则OD的票价小于组成此OD的各区段的票价之和。式( 8 )表示OD的票价应大于组成此OD的各区段的票价之和减去任意区段的票价。式( 9 )是票价的整数约束。

2 模型求解

由于需求函数中存在随机误差项εijt，因此模型(M1)的最优解会受到随机误差项的影响。如果不能准确估计式( 1 )中随机误差项εijt的分布，则得到的最优解可能不满足列车运输能力的限制，从而达不到收益最大化的目的。实际上，为了得到稳健最优解(Robust Optimization)，不必满足所有情况下的约束条件，可以在某个缩小的随机误差项变化范围内求得最优解，这样得到的解不仅能适应随机误差项的变化，而且目标函数的值也不至于过多地损失。为此，本文引入稳健优化模型方法[11]，在假设已知随机误差项εijt的变动范围而不知道其确切分布时，在解的稳健性和目标函数的最优值之间寻求平衡，来适应需求的不确定性。

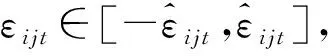
(10)

引入参数Δij，Δij为给定的非负实数，用来约束OD对(i,j)各时段实际总需求与名义总需求的偏离程度，则有

(11)

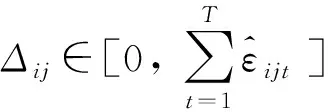
因此，考虑需求函数的不确定性，将式(10)、式(11)带入模型(M1)中，并且在目标函数中增加由随机误差引起的收入变化量的最小值达到最大的一项，可以将模型(M1)转化为动态定价稳健模型(M2)，即

(12)

s.t.

(13)

(14)

(15)

ξijt≤1

(16)

(17)

若lek>lij，则

pekt>pijt∀t,∀(e,k),(i,j)∈F

(18)

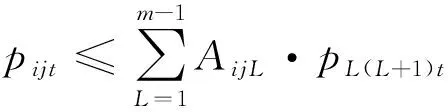
(19)

若Ω=L|(i,j)∈F且AijL=1则

∀t，∀g∈Ω

(20)

pijt∈N

(21)

在模型(M2)中约束条件式(13)为

约束条件式(14)为

合并约束条件式(13)和式(14)，则约束条件式(13)可以松弛为

通过变换可以将模型(M2)松弛为稳健模型(M3)，即

(22)

s.t

(23)

ξijt≤1

(24)

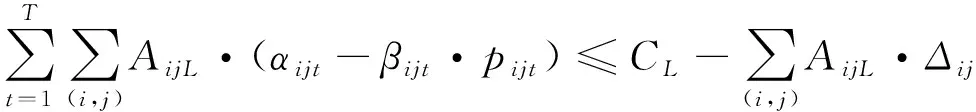
(25)

(26)

若lek>lij，则

pekt>pijt∀t,∀(e,k),(i,j)∈F

(27)

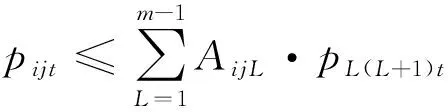
(28)

若Ω=L|(i,j)∈F且AijL=1则

∀t，∀g∈Ω

(29)

pijt∈N

(30)

模型(M3)为一个两层规划问题，其内层最小化问题可以认为是决策变量为ξijt的线性规划，约束条件式(23)、式(24)为内层规划问题的约束，通过求解内层规划的对偶问题，并利用强对偶定理可以将模型(M3)转化为如下凸规划问题模型(M4)：

(31)

s.t.

(32)

(33)

(34)

若lek>lij，则

pekt>pijt∀t,∀(e,k),(i,j)∈F

(35)

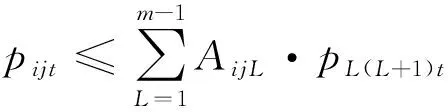
(36)

若Ω=L|(i,j)∈F且AijL=1则

∀t，∀g∈Ω

(37)

pijt∈N

(38)

wij≥0

(39)

在模型(M4)中，wij为模型(M3)中内层规划的对偶问题的决策变量。

通过求解模型(M4)，可以得到客票预售期内每个时段每个OD的最优定价，继续利用式( 1 )便可求得每个时段每个OD的票额分配结果。

3 案例分析

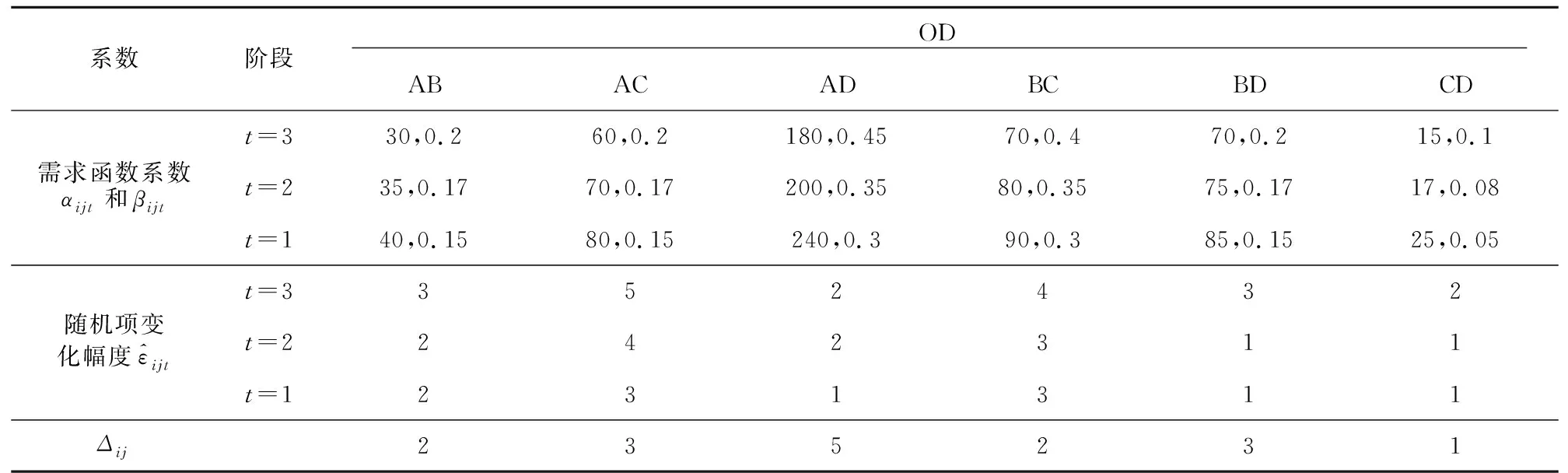
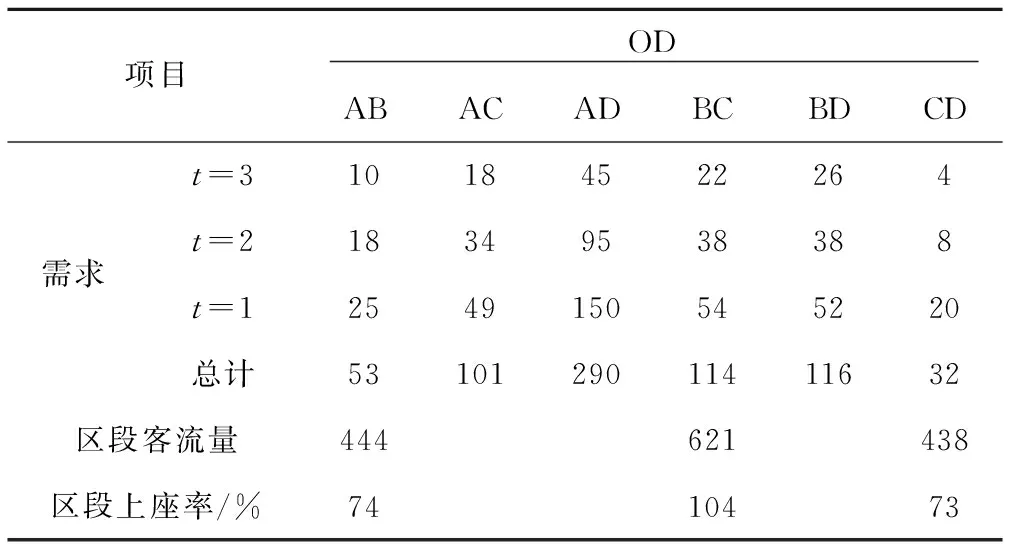
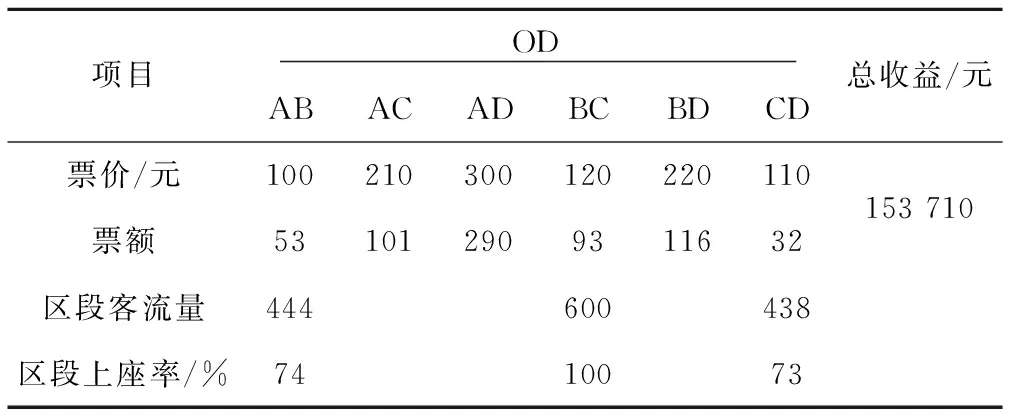
根据文献[17]的数据，假设某高速列车运行线路包含4个客运站3个区段，见图2。列车在该线路的客运站上均有客运作业。假设列车的定员为600人，即CL=C=600，根据《关于动车组票价有关事项的通知》中的规定，目前票价可以上下浮动10%。则各OD票价及其上下限如表1所示，各OD距离大小关系为lAB

表1 各OD票价及其上下限取值元

本文将客票预售期分为3个阶段，即t=1,2,3，t越小表示越接近列车发车时间，需求函数系数αijt随t的增大而减小，βijt随t的增大而增加，表示越临近发车时间，旅客需求对价格的敏感性越低，这符合收益管理思想[10]，即在售票初期(t=3)由于人们不能确定出行时间所以需求量较小，因此售票初期αijt值较小，而此时旅客的敏感性较高，因此售票初期βijt值较大，可以通过降低票价来吸引客流。

根据收益管理思想和文献[17]中全价票下需求函数的关系，将客票预售期分为3个阶段，给出不同售票阶段各OD的需求函数系数及其随机项变化幅度，并在假定铁路管理部门掌握一定的需求信息后，给出Δij的取值，见表2。

表2 系数取值

如果铁路管理部门在售票时不考虑不同售票阶段旅客对价格的敏感性，在每个售票阶段都以单一全价票的方式进行客票销售，则根据表2中不同售票阶段的需求函数关系，在全价票下各OD的需求及各区段上座率见表3。

表3 单一全价票下各OD需求及区段客流量

表3中可以看出，在以单一全价票进行客票销售时，BC区段的客流需求超过了列车的定员，表明列车的运输能力不能满足所有旅客的需求。利用文献[14]中的票额分配模型，以收益最大化为目标，根据全价票下各OD的客流需求，得到的票额分配方案如表4所示。利用Lingo12.0对本文所建模型(M4)进行求解，得到的动态定价与票额分配方案见表5。

表4 单一全价票下票额分配方案

表5 动态定价和票额分配方案

对比表3和表4，可以看出在以单一全价票对客票进行销售时，由于票价固定，各OD间的需求是一个定值，在此需求下，根据各区段上座率可以看出，列车的运输能力并不能满足所有旅客的需求，因此在以收益最大化为目的进行票额分配时，通过减少OD对BC间的票额数来限制BC间的客流需求，使得各区段的客流量都不超过列车定员，这种方式由于限制了部分旅客的需求，可能会造成旅客满意度的下降，此种方式下获得的收益为153 710元。

表5是在考虑不同售票阶段旅客对价格的敏感性不同，根据本文所建的模型求得的动态定价和票额分配方案，可以看出通过调整不同售票阶段的票价，各OD间的需求发生了变化，各区段的客流量都不超过列车定员。售票初期由于旅客对价格的敏感性较高，票价相对较低可以吸引一部分客流，但是分配的票额数相比开车前分配的票额数较少，这也符合收益管理的思想，为了获得更多的收益，把票额留给愿意支付更高价格的旅客。OD对AC、BC、BD在售票初期票价高于全价票，说明这3个OD对间的客流需求比较旺盛。此方案下可以获得的收益为160 682元。与表4相比，利用本文模型求得的动态定价和票额分配方案能够获得更多的收益，但各区段的上座率并没有提高，这也说明了并不是将车票卖的越多能够获得的收益越大，而是将车票卖给愿意支付更高价格的旅客才能获得更多的收益。同时，通过调整不同售票阶段的票价，来调节各OD间的客流需求从而可以获得更多的收益，相比单一全价票情况下利用分配的票额数来限制客流的需求，动态定价方式是通过调整票价来主动引导客流需求的变化，更符合旅客的心理需求。通过对比，可以看出利用本文模型计算出来的方案可以获得更多的收益，从而验证了采用动态定价相比现有的单一票价较优，并且模型中考虑了需求的波动，使得计算出来的票额分配方案能够适应实际需求在一定范围内的波动，避免了实际需求波动较大时，导致方案不可行，给现场带来大量的票额调整工作。然而，由于目前高速铁路动态调整票价仍处于探索阶段，需求随票价变化的关系需要不断地在实践中积累，因此在运用本文模型时需要根据实践对需求函数及其需求波动情况不断地进行改进。

4 结束语

本文基于收益管理理论，对不确定需求下的高速铁路单列车的动态定价与票额分配方法进行了研究，根据客票预售期不同阶段客流需求的特点为各OD车票制定价格并分配相应的票额，在模型中考虑了需求的波动，使得到的方案能够适应实际需求的波动，避免了实际需求波动较大时导致方案不可行。通过算例，并与单一全价票下的票额分配方案对比，结果表明动态调整票价不仅可以调节客流，还可以提高收益，从而验证了模型的可行性与可操作性。本研究为高速铁路票价制定提供了一个新的方法，但仅研究了单列车的情况，此外旅客对票价的敏感性及其客流需求的波动情况需要根据长期的运输实践来获得，今后将进一步研究多列车、多条运输线路及其考虑旅客选择行为的更加符合实际情况的高速铁路动态定价与票额分配问题。