低周疲劳下考虑累积塑性应变的裂纹板裂纹闭合效应研究

杨 平， 彭 子 牙， 姜 伟， 余 志 锋， 胡 康

(1.武汉理工大学 高性能船舶技术教育部重点实验室， 湖北 武汉 430063；2.武汉理工大学 交通学院， 湖北 武汉 430063 )

0 引 言

随着船舶大型化的发展，船舶结构承受越来越高的应力和大变形的低周疲劳损伤.在循环荷载作用下，裂纹板裂纹尖端附近区域出现严重的应力集中并达到材料的屈服条件时，裂纹尖端附近的区域会产生塑性应变并逐渐累积，引起裂纹尖端塑性区内结构材料刚度降低，最终导致结构破坏.在裂纹扩展过程中，当裂纹逐渐穿过前方塑性区时，原裂纹尖端塑性区的包络线和裂纹面将会形成塑性尾迹区，塑性尾迹区的残余塑性变形形成的残余压应力会引起裂纹闭合，裂纹闭合后影响了裂纹尖端附近区域应力-应变场的分布，从而降低了应力强度因子范围，减缓了裂纹扩展，因此考虑裂纹闭合对裂纹扩展寿命的准确评估是十分有必要的.低周疲劳下塑性变形仍然是诱发裂纹闭合的主导因素，且裂纹闭合与裂尖塑性变形有着密切联系，探讨考虑裂尖累积塑性应变的演化对低周疲劳下裂纹闭合效应复杂机理的研究以及裂纹扩展规律探讨显得十分有意义.

断裂面的相互作用导致了裂纹尖端应力强度下降和疲劳寿命的增加，Elber[1]在断裂力学参数方面讨论了这一概念，对与疲劳裂纹闭合相关的力学现象进行了大量的研究工作.目前提出的闭合机理有塑性区诱发的闭合效应(PICC)、氧化物诱发的闭合效应(OICC)、裂纹表面粗糙度诱发的闭合效应(RICC)等.但大量的研究表明，塑性引起的裂纹闭合已经被广泛接受为影响疲劳裂纹扩展速率的主要闭合机理之一[2-3].Newman等[4]认为裂纹尖端上下表面在裂纹扩展阶段发生接触时，会降低裂纹尖端应力强度因子的范围，从而降低裂纹扩展速率，这种现象被称为塑性区诱发的裂纹闭合，主要是裂纹面塑性尾迹区内的残余塑性变形产生的压缩残余应力阻碍了裂纹尖端上下表面张开.此外，许多学者在裂纹闭合研究方面也进行了大量的试验和数值模拟，取得了突出性的成果.Antunes等[5]对MT试件进行了试验研究，通过获得的柔度曲线得出不同裂纹长度下对应的张开荷载并确定了裂纹闭合参数，通过建立的有限元模型，研究了节点释放间隔循环次数、网格划分等因素对裂纹闭合水平的影响，并将相关结果与试验进行对比，发现比较吻合.Borrego等[6]以AlMgSi-T6铝合金材料MT试件为试验对象，基于裂纹扩展理论，通过引入有效应力强度因子范围，分别研究了不同应力水平下，裂纹闭合效应对裂纹扩展速率的影响.Wang等[7]认为研究过载效应必须合理考虑裂纹尖端应变的演化，通过对比试验测得的裂纹张开位移及裂尖应变，发现裂纹尖端应变的演化与裂纹张开位移的变化相似，但并未研究尾迹区与裂纹尖端应变演化的联系.此外，Antunes等[8]通过研究裂纹面的接触与非线性裂纹尖端参数(循环塑性应变的范围、裂纹尖端张开位移、循环塑性区尺寸等)的联系，来验证裂纹闭合概念的有效性，并得出裂纹闭合对控制疲劳裂纹扩展速率的裂纹尖端参数有很大的影响，接触减小了不同的裂纹尖端参数的值.

目前对于裂纹闭合效应的研究在低周疲劳条件下含裂纹船体板的裂纹扩展规律方面很少触及，而考虑裂纹尖端累积塑性应变演化与裂纹闭合效应之间的联系仍是有待解决的问题.本文基于弹塑性断裂力学理论及裂纹闭合理论，以船用高强度钢板AH32为研究对象，通过数值模拟及相关试验研究，从应力比、裂纹长度、循环次数等几个方面展开探讨，通过得出的结果较为全面地分析裂纹尖端累积塑性应变的演化与裂纹闭合效应及残余尾迹区之间的交互影响，以期为低周疲劳下船体裂纹板裂纹闭合效应的复杂机理研究提供一种新的途径.

1 理论公式

在裂纹闭合效应研究方面，裂纹闭合参数U常用来表征裂纹闭合水平的大小，其表达式为[9]

(1)

有效应力强度因子的范围ΔKeff表达式如下：

ΔKeff=Kmax-Kop=UΔK

(2)

式中：Pop为裂纹张开荷载；U越小，裂纹闭合效应越强.

2 低周疲劳试验研究

2.1 试验材料与试验工装

本试验以AH32船用钢板为研究对象，模型的尺寸如图1(a)所示，总长Ltot=560 mm，宽度Wtot=200 mm，厚度t=3 mm，预制裂纹长度a0=16 mm，其定位圆孔尺寸详见图1(a).对于承受荷载的有效区域采取圆弧过渡形式，且圆弧半径R=50 mm，如图所示，有效区域长度Leff=200 mm，宽度Weff=100 mm.采用MTS322电液伺服疲劳试验机进行低周疲劳试验，施加的最大荷载Pmax=95 kN(σmax=316.67 MPa)，应力比范围为0～0.3，试验加载频率为1 Hz，试验工况如表1所示.如图1(d)所示，为了测得裂纹张开位移，将电子引伸计固定在裂纹左右两边的高强磁铁之间，以防止滑移，且间距d=10 mm.对于裂纹的整个扩展过程，通过高倍电子显微镜在板的另一侧进行录像观察.

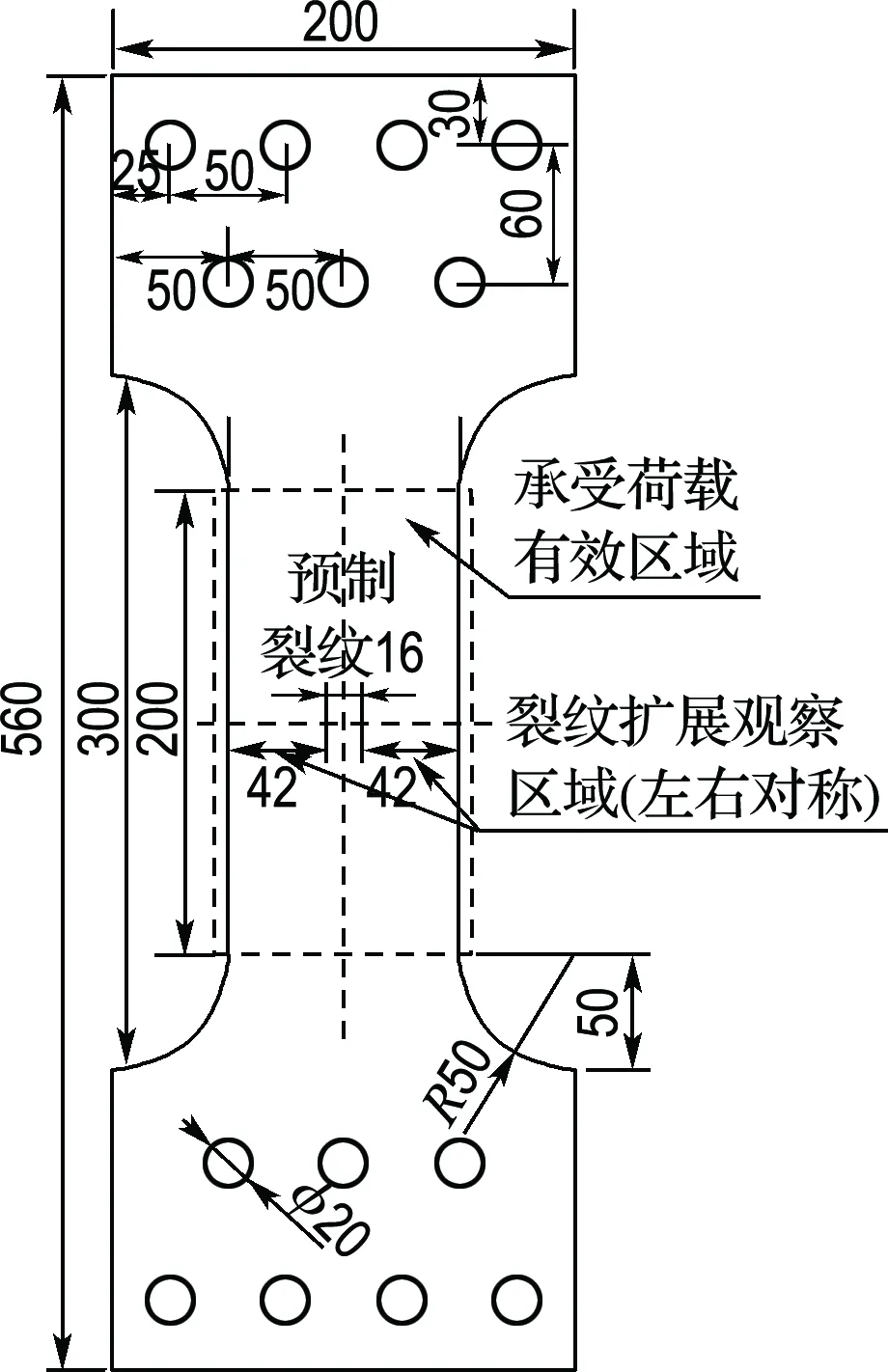
(a) 试件模型

(b) 试件工装

(c) 试件断口

(d) 引伸计安装示意图

图1 试件模型试验

Fig.1 Specimen model test

表1 试验工况

2.2 裂纹张开荷载确定方法

通过实验获得的荷载-位移(P-V)曲线，采用最大相关系数的方法推导出不同裂纹长度下对应的张开荷载Pop.该方法提取P-V曲线数据的上半部分并计算最小二乘相关系数，然后添加下一个数据对，并再次计算相关系数，对整个数据集重复该过程，相关系数达到最大值的点对应的荷载则定义为裂纹张开荷载Pop[5].

3 有限元分析

本文以AH32船用钢板为研究对象，采取有限元软件ABAQUS进行建模分析，模型范围选取承受荷载的有效区域.由于对称性的条件，建立1/4模型，L=100 mm，W=50 mm，a0=8 mm，计算模型如图2(a)所示.为了较好地模拟裂纹的闭合效应及裂纹扩展，在模型下端建立一条解析刚性线作为主接触面，模型底部表面作为从接触面.模型网格采用CPS4R平面应力四节点减缩积分单元进行网格划分，如图2(b)所示，扩展区域采用细化网格，网格尺寸为0.05 mm×0.05 mm，以保证循环塑性区至少包含3～4个单元[10].

(a) 1/4有限元模型

(b) 细化区网格

目前大多数的研究认为低周疲劳下塑性变形仍是诱发裂纹闭合效应的主要因素，由于裂纹闭合效应是一种基于塑性变形的现象，准确地模拟材料的屈服和硬化行为十分重要.Chaboche组合强化模型能较好地模拟平均应力松弛、棘轮效应、包申格效应、安定性等材料塑性特性，因此本文采用Chaboche组合模型，其参数可以通过数值模拟与试验的应力-应变曲线拟合得出，如表2所示，其中ν为泊松比，Q为屈服面的最大变化值，b为屈服面随塑性应变增加的变化率，c1、c2、c3为初始随动强化模量，γ1、γ2、γ3决定背应力随塑性应变增加的速率.

表2 Chaboche组合模型材料参数

本文采用节点释放技术来模拟裂纹动态扩展的过程，由于考虑到释放节点时机与计算时间的影响，本文采取文献[11]的方法，每隔两个循环且在最小荷载处释放一个节点，裂纹张开荷载通过观察裂纹尖端后第一个节点y方向的位移大小来确定，即节点y方向的位移由零增大的瞬时时刻对应的外加荷载定义为裂纹张开荷载.在平面应力的条件下，模型的边界条件取为沿y轴方向施加x方向的固定约束，沿x轴方向定义一条刚性线，并在裂纹终止扩展的区域施加y方向的固定约束[12].采用最大外荷载Pmax=95 kN(σmax=316.67 MPa)，应力比为0～0.4等几种不同加载方式，在模型的上端施加均布荷载.为准确捕捉裂纹的张开(闭合)点，采用固定增量步的形式，考虑到计算时间的影响，裂纹每次扩展到5 mm就停止计算.

3.1 裂纹尖端应力-应变曲线

当裂纹向前扩展时，每一个裂纹尖端前的塑性变形都在不断地累积，高斯点能很好地反映塑性变形累积的过程.当裂纹扩展到某裂尖高斯点前时，裂尖对应的塑性变形开始下降，随即出现的变形即为残余塑性变形的一部分，不同裂纹长度对应的应力-应变响应是不同的，如图3所示，为不同的裂纹长度下对应的应力-应变演化形态.

3.2 裂纹张开荷载与裂纹闭合参数分析

(a) 沿裂纹面高斯点

(b) Δa=0.1 mm

(c) Δa=0.2 mm

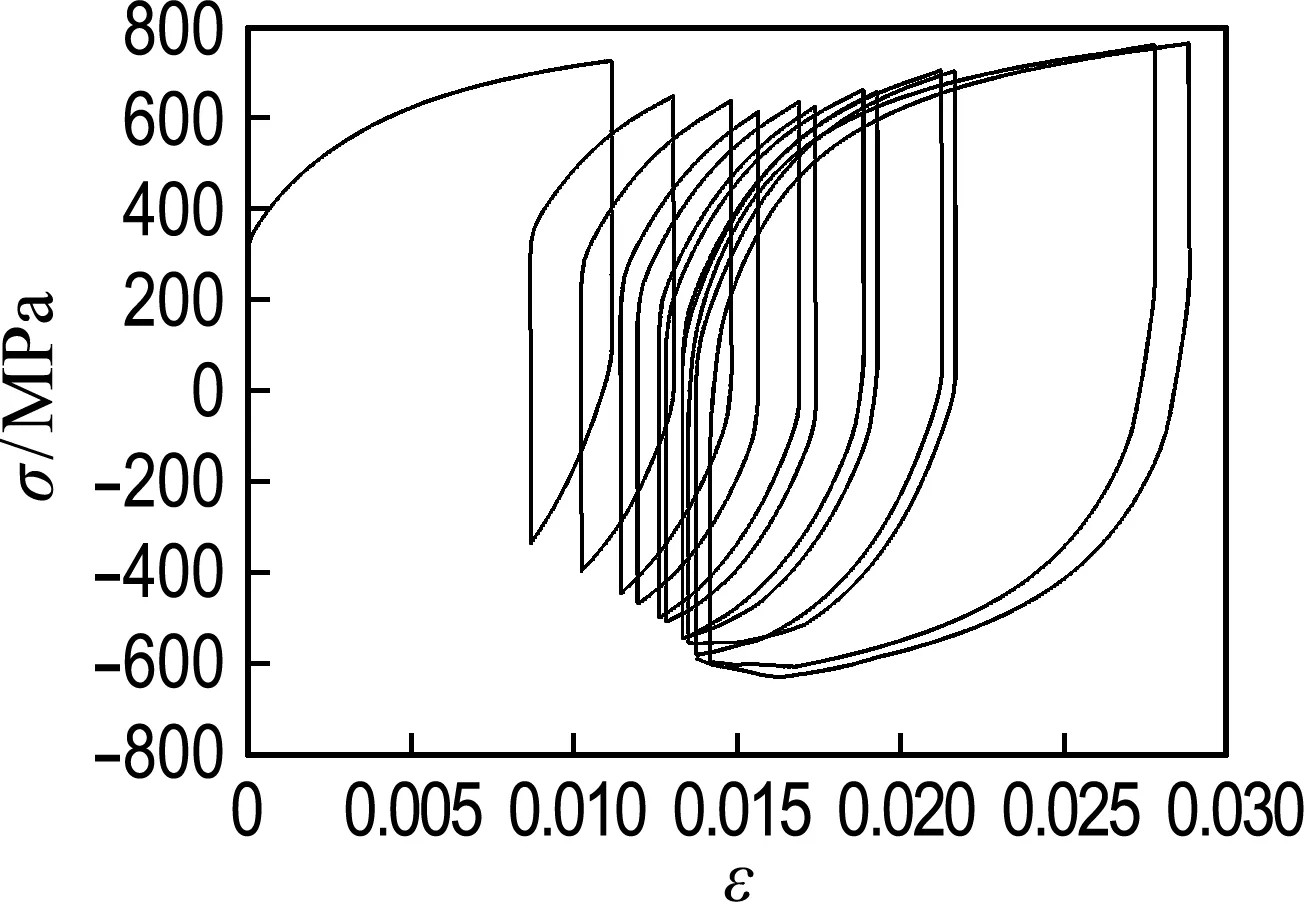
(d) Δa=0.3 mm

图3 不同位置处应力-应变演化形态

Fig.3 Stress-strain evolution at different locations

通过船舶裂纹板低周疲劳裂纹闭合效应试验以及数值模拟，对试验与数值模拟的结果进行了对比分析，如图4、5所示.从图中可以看出数值模拟的结果趋势大致与试验得出的结果相似，图4表明裂纹张开荷载随着裂纹长度的增加而增大，然后逐渐趋于稳定，当裂纹达到一定的长度时，张开荷载呈现缓慢的下降趋势，且应力比越大，裂纹张开荷载也越大.通过获得的Pop，利用式(1)，可以求得对应的U，如图5所示，即为不同应力比下裂纹闭合参数变化曲线.可以看出，应力比越大，U越大，裂纹闭合效应越弱，这主要因为应力比的增加导致最小应力也增加，增加的最小应力会抵消裂纹面上的部分残余压应力，使得促进裂纹闭合的残余压应力减小，裂纹闭合效应减弱.

从图4、5中可以看出，试验与数值模拟结果存在一定误差，数值模拟出的闭合效应比试验明显，在应力比增加的情况下，Pop的平均误差分别为9.28%、8.49%、6.77%、5.82%，U的平均误差分别为3.61%、3.98%、4.11%、4.43%，可以看出，尽管存在一定的误差，但数值模拟的方法仍然具有一定的可行性.产生误差的原因主要有[13]：(1)数值模拟的是理想裂纹，未考虑扩展中裂尖钝化，而试验中钝化现象会影响裂纹的闭合水平.(2)试验中引伸计距离裂纹尖端的距离较远，会导致引伸计不敏感，从而使测得的结果偏小.除此以外，加工工艺以及试件的初始缺陷(残余变形等)也是导致误差的重要原因.

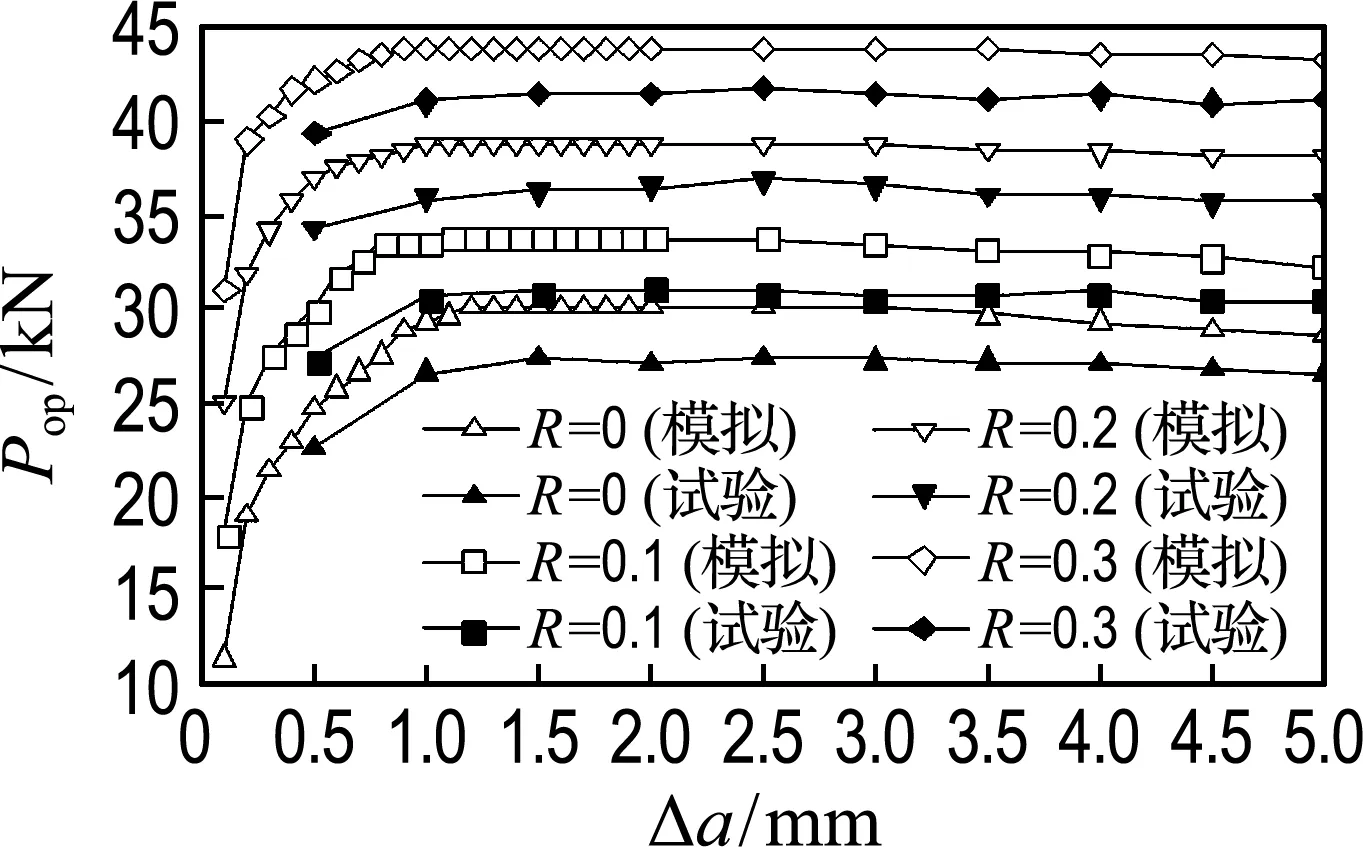
图4 张开荷载与裂纹长度的关系

图5 裂纹闭合参数与裂纹长度的关系

4 累积塑性应变与裂纹闭合参数的关系

4.1 裂纹闭合机理与裂尖累积塑性应变演化研究

4.1.1 裂纹闭合机理探讨 裂纹的闭合效应与裂尖累积塑性应变有着紧密的联系，如图6所示，裂纹在扩展的过程中，裂纹前方的塑性区对尾迹区的形成有着影响，而裂纹的闭合效应同时也影响着裂尖附近区域应力-应变场的分布，减缓了裂纹扩展.可以认为裂尖累积塑性应变对裂纹闭合有两种影响：一是当前裂纹长度下，塑性应变的累积对裂纹闭合效应的影响；二是裂纹扩展后，前一裂纹尖端形成的不可恢复变形对下一裂尖尾迹区的残余压应力场的影响，从而影响裂纹闭合效应.

图6 裂纹尖端区示意图

在裂纹开始扩展阶段，如图7所示，裂尖累积塑性应变达到峰值，随后不同位置处的裂尖累积塑性应变呈现下降的趋势，这主要与先前的硬化有关[14].从图7中可以看出，初始峰值对裂纹闭合有一定的促进作用，随着裂纹的扩展，残余尾迹区逐渐形成，此时裂纹闭合主要由裂尖尾迹区产生的残余压应力场作用产生.初始扩展阶段，裂尖累积塑性应变先减小然后趋于平稳，且裂纹闭合参数也减小后趋于平稳，可以看出二者稳定的位置大致上相同，这说明裂尖累积塑性应变的稳定与裂纹闭合效应的稳定有着密切的联系.当裂纹继续扩展时，裂尖累积塑性应变缓慢增加，但裂纹闭合参数仍然保持不变；当裂纹扩展到一定的长度后，裂尖累积塑性应变较大，裂纹闭合参数开始呈现缓慢上升的趋势.在相关研究中[15]，裂纹扩展长度较长时，才有可能出现闭合效应降低的情况，但其应力水平较低，而本文是低周疲劳循环荷载，应力水平较高，因此可以认为较高的应力水平可能会促使闭合效应降低的情况提早发生.

(a) εp-Δa

(b)U-Δa

图7 累积塑性应变和裂纹闭合参数与裂纹长度的关系

Fig.7 Relationship between accumulative plastic strain and crack closure parameter and crack length

4.1.2 残余压应力场的演化 裂纹面的闭合部分从某种程度上可以认为承担了部分荷载，致使裂尖的应力-应变场降低，塑性应变的累积程度也降低；而当前裂尖累积塑性应变的增大，会促使裂纹接触应力降低，裂纹闭合效应也降低，二者相互影响.由于尾迹区残余压应力场的大小是影响裂纹闭合水平的主要因素，研究裂尖累积塑性应变与尾迹区的残余压应力场的联系，能间接地反映裂尖累积塑性应变对裂纹闭合效应的影响.

在应力比R=0的情况下，本文探究了在最小荷载下不同的裂纹扩展长度(Δa=0.6，1.2，1.8，4.5 mm)的裂尖附近应力分布情况.结合图8及表3探讨了3种阶段下(初始阶段、稳定阶段、最后阶段)裂尖累积塑性应变与尾迹区残余压应力场之间的联系.如图8(a)所示，对处于初始阶段与稳定阶段下的裂纹扩展长度进行了比较，此阶段内裂尖累积塑性应变在不断减小后趋于平稳，但残余压应力场整体上是在增大，且相对增加量Δσ为54%，这与裂纹闭合参数减小、闭合效应增强的结果十分吻合.如图8(b)所示，对处于稳定阶段的裂纹扩展长度进行了比较，此阶段内累积塑性应变值趋于稳定，变化不明显，可以看出其所对应的残余压应力场也大致相似，相对增量仅为7.9%，对裂纹闭合效应影响不明显，裂纹闭合参数也趋于稳定.如图8(c)所示，对处于稳定阶段与最后阶段下的裂纹扩展长度进行了对比，此阶段内裂尖累积塑性应变不断增大，当增大到一定的程度时，裂尖后方的残余应力场会出现缓慢的减小，相对增量为-18%，这是导致后期裂纹闭合效应减弱的主要原因.从以上分析可知，尾迹区的残余压应力场能很好体现裂纹的闭合水平，当裂尖累积塑性应变不断增大时，会使裂尖后方残余压应力场降低，这主要是由于荷载循环过程中抵消掉了裂纹面的部分残余应力.

4.2 应力比的影响

(a) 初始与稳定阶段

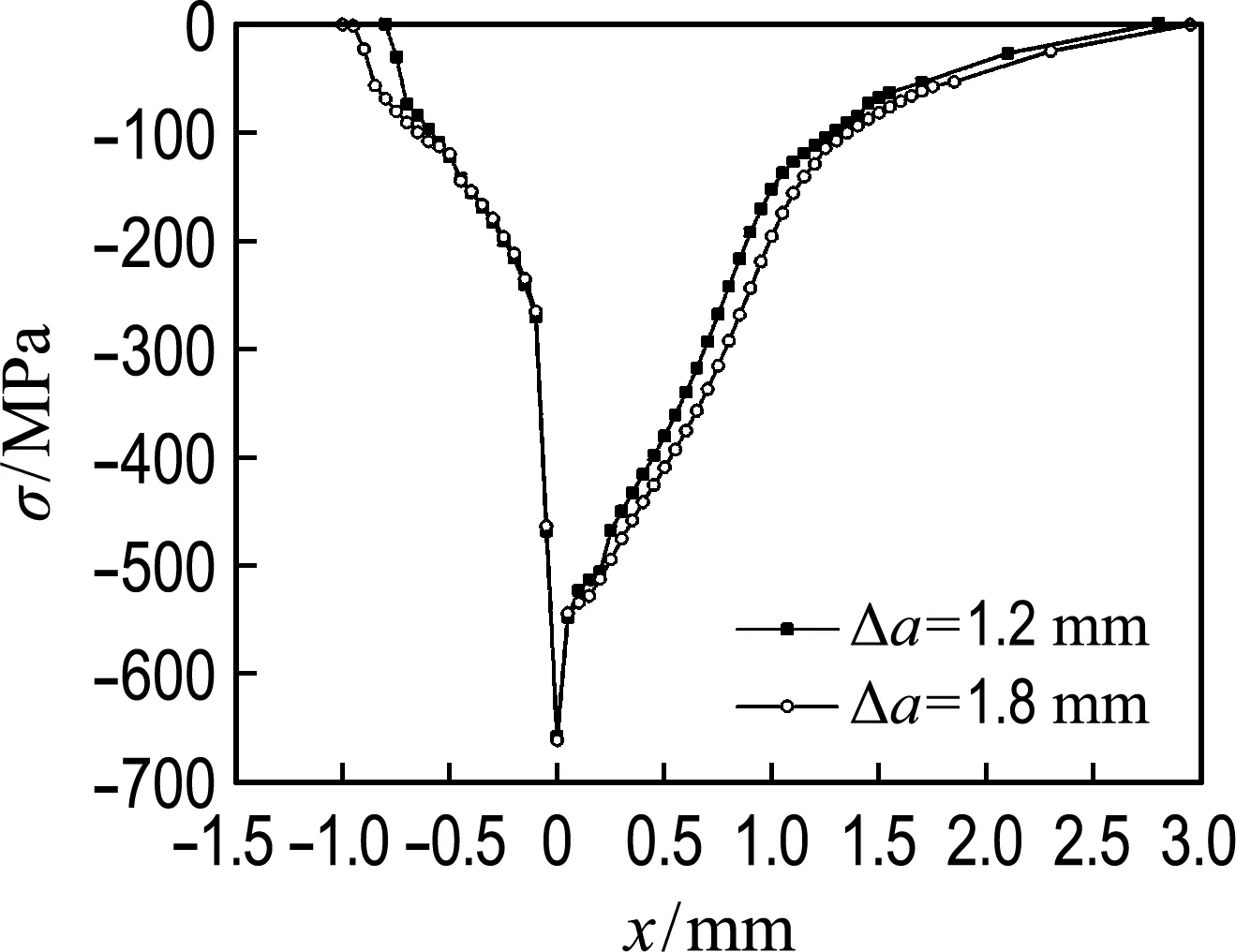
(b) 稳定阶段

(c) 稳定与最后阶段

图8 最小荷载处裂纹尖端附近应力分布

Fig.8 Stress distribution near crack tip at the minimum load

表3 不同裂纹长度下的残余压应力场演化

本文探讨了不同应力比下裂尖累积塑性应变与裂纹闭合参数的关系，选取应力比为0.1、0.3、0.4进行了分析.如图9所示，应力比越小，闭合参数越小(U稳定值分别为Ust(0.1)=0.717，Ust(0.3)=0.771，Ust(0.4)=0.820)，累积塑性应变下降的范围也越大(Δεp(0.1)=1.289 5%，Δεp(0.3)=1.040 4%，Δεp(0.4)=0.948 6%)，可以认为裂纹闭合效应的增强会促使裂尖累积塑性应变的降低，且裂尖累积塑性应变与裂纹闭合参数也相对越晚趋于稳定.由于裂纹长度的影响，最后阶段裂纹扩展到一定长度时，裂尖累积塑性应变增加量较大，会在一定程度上促使裂纹闭合效应降低，从而后期出现裂纹闭合参数缓慢增大的情况，这主要是因为裂尖后方残余压应力场有所减小.如图10所示，裂纹扩展长度为2 mm时，随着应力比的增大裂尖累积塑性变形也增加(εp(0.1)=2.561 7%，εp(0.3)=2.727 6%，εp(0.4)=2.829 2%)，再加上最小应力增加的共同作用，导致裂尖后方的残余压应力场整体降低(σre(0.1)=-2 413.34 MPa，σre(0.3)=-1 080.5 MPa，σre(0.4)=-838.741 MPa)，使得裂纹闭合效应降低.

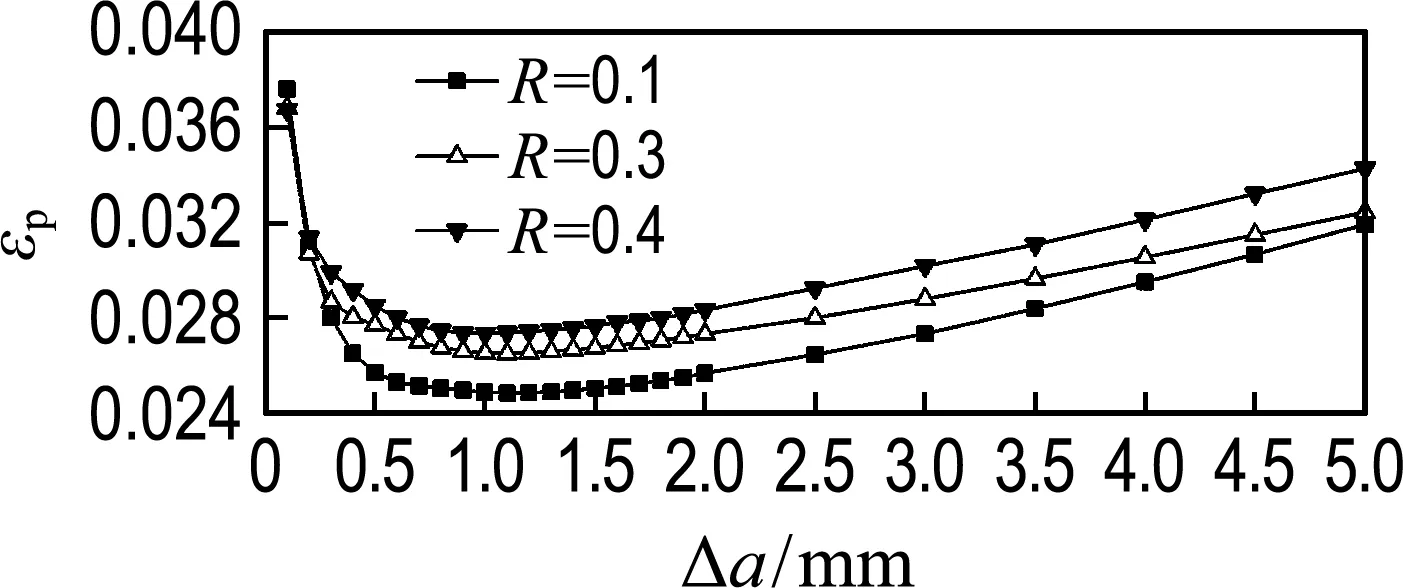
(a) εp-Δa

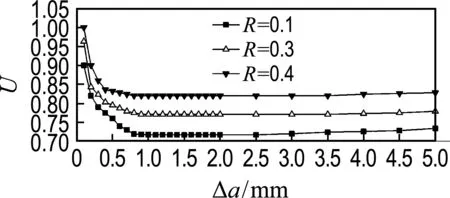
(b)U-Δa

图9 应力比的影响

Fig.9 The effect of stress ratio

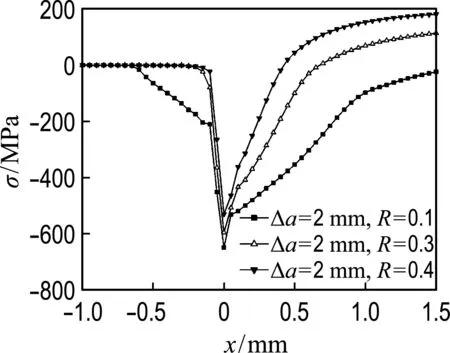
图10 不同应力比下最小荷载处裂尖附近应力分布

4.3 循环次数的影响

循环次数对裂纹的闭合效应、裂尖累积塑性应变及残余压应力场有着不可忽略的影响，因此本文选取了应力比R=0，循环次数为2、5、10共3种情况，考虑计算时间的影响，裂纹只扩展1 mm，以此来探究循环次数的影响.如图11所示，循环次数越大，裂纹闭合参数越小，这主要是扩展过程中循环次数的增加会一定程度降低裂纹面的残余压应力，且初始裂尖的累积塑性应变随着循环次数的增加而减小，随着裂纹长度的增加，下降的幅度也较小(Δεp(2)=1.351 7%，Δεp(5)=1.145 1%，Δεp(10)=0.892 8%)，这主要是由于裂纹闭合效应整体降低，其对裂尖累积塑性应变的抑制作用也减小.从图12可以看出，裂纹扩展长度为0.5 mm时，循环次数增加，裂尖后小范围(0～0.1 mm)的残余压应力也增加，但整个残余压应力场仍然较小(σre(2)=-1 889.56 MPa，σre(5)=-1 541.67 MPa，σre(10)=-1 400.00 MPa)，导致裂纹闭合效应降低.从以上分析可知，在一定的裂纹长度下，荷载循环次数增加，裂纹闭合效应会降低，且裂尖累积塑性应变也增大，裂纹易向前扩展，这与试验是十分吻合的.

(a) εp-Δa

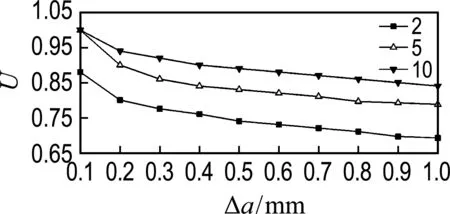
(b)U-Δa

图11 循环次数的影响

Fig.11 The effect of number of cycles

图12 不同循环次数下最小荷载处裂尖附近应力分布

Fig.12 Stress distribution near crack tip at the minimum load under different numbers of cycles

5 结 论

(1)裂纹扩展过程中，裂尖的累积塑性应变增加，会一定程度上使裂尖后方残余压应力场降低，导致裂纹的闭合效应降低；裂尖的累积塑性应变下降的幅度越大，说明尾迹区的残余压应力场越大，裂纹闭合效应越强.当裂纹闭合效应增强时，裂尖应力-应变场减弱的程度相对增大，裂尖的塑性变形一定程度降低，二者是相互作用的关系.

(2)应力比越大，裂纹闭合效应越弱，且累积塑性应变与裂纹闭合参数相对越早趋于稳定，裂尖累积塑性应变整体水平较高，尾迹区的残余压应力场整体较小，这是应力比增大导致裂纹闭合效应降低的主要原因.

(3)循环次数的增加，裂尖累积塑性变形下降幅度的减小，间接说明尾迹区的残余压应力场增大的幅度较小，裂纹闭合效应小幅度增强，且一定裂纹长度下，较多的循环次数会使裂尖后方压应力场降低，裂纹闭合效应减弱.

(4)裂纹扩展初期，随着裂纹长度的增加，裂纹闭合效应逐渐增强，然后趋于平缓，当裂纹长度继续增加到一定程度时，在低周疲劳循环荷载下，裂纹闭合效应可能会提前发生缓慢减弱的情况.