表演水池鱼跃浪压力计算与试验

2018-07-23迟世春，生光辉，贾宇峰*

大连理工大学学报 2018年4期

迟世春，生光辉，贾宇峰*

(1.大连理工大学海岸和近海工程国家重点实验室，辽宁大连 116024；2.大连理工大学建设工程学部水利工程学院工程抗震研究所，辽宁大连 116024 )

0 引言

海洋馆里的表演水池一般安装透明的亚克力板，以便游客观赏海洋动物水中及跃起的运动姿态.亚克力板一般属空间弧形悬臂结构，尽管挡水高度不大，但跨度很大，在池内水压力作用下会产生较大的变形.目前，国外主要通过设置悬臂式腹臂提高其抵抗向外变形的刚度，但腹臂会遮挡游客的视线，影响观赏效果.因此，国内有业主提出不设置腹臂，此时亚克力板的变形控制问题凸显出来.国内某海洋世界拟引进鲸鱼表演项目，其表演水池长约50 m，宽约30 m，深约11 m，平面上呈对称的类椭圆形.表演水池侧壁的底部为防水的钢筋混凝土墙，顶部有4块亚克力板镶嵌于池边.亚克力板挡水区高2.3 m，长板长19 m，短板长14 m.水池中最多有4条虎鲸同时表演.虎鲸体形庞大，重达6 t ，泳速最高可达55 km/h，最高可跃出水面5 m.虎鲸表演落水时拍打水面，形成涌浪作用在直立水池壁上，对亚克力板形成波浪动水压力.在动水压力作用下，亚克力板产生垂直于池壁的振动变形.若变形过大，导致亚克力板失稳，将直接危及游客生命安全.

计算亚克力板的变形首先要研究作用在亚克力板上的荷载，荷载包括静水压力和动水压力.其中，静水压力是固定和已知的，而虎鲸表演时产生的波浪动水压力则需要深入研究给出.目前水利行业关于涌浪对直立壁动水压力的研究文献极少，也没有涌浪作用下动水压力的通行算法，在计算分析时主要参考海港部门的研究成果.《水工建筑物荷载设计规范》(DL 5077—1997)[1]给出了直墙式挡水建筑物上浪压力的计算方法.但是作为计算浪压力的关键参数，波浪三要素的求解方法没有给出.《海港水文规范》(JTS 145-2—2013)[2]给出了波浪对直墙式建筑物浪压力的计算方法，以及风浪和涌浪三要素的计算方法.华艳茹[3]总结了波浪正向入射对直墙作用力的研究成果，通过试验对比了各种计算方法的特点和适用范围.虽然，计算直墙前波浪压力的方法较多[4-10]，但这些波浪压力计算方法基本都是基于风致波浪，而非动物表演涌浪引起的波浪.二者的区别在于计算浪压力的参数不同，也就是动物表演涌浪三要素有待研究.

本文从波浪理论[11]角度出发，运用斯托克斯波的二阶近似解和直墙前立波的五阶近似解中波高与波长的关系求解动物表演涌浪情况下涌浪三要素的近似解.根据《水工建筑物荷载设计规范》和《海港水文规范》方法对直墙前波浪压力进行计算，并通过试验给予验证.最后采用有限元数值方法模拟亚克力板的受力变形，并与试验结果进行比较.

1 涌浪的波浪要素

计算动水压力首先要确定参数——涌浪三要素，即波高(H)、波长(L)和周期(T).动物表演涌浪与风浪产生的机理不同，风浪是风吹水面引起的，风速是计算风浪三要素的基本量.涌浪是由一定体积的物体以一定的速度扰动水体变形而产生的[12]，所以不能直接引用风浪三要素的计算方法.根据统计资料，动物表演涌浪呈现明显的非线性、周期性和接近摆线的形状等基本特征，其波长范围在几米至十几米，且满足d/L>0.5(d为水深，d=11 m，L为波长)，此时池底不影响波浪传播，涌浪的水波为深水波.因此，本文中根据普遍适用的波浪基本理论，选用深水斯托克斯波来描述动物表演涌浪.选用深水斯托克斯波的另一个原因是其波浪中心线对静水面超高公式涉及未知量少，对求解动物表演涌浪三要素是有利的.

斯托克斯波的二阶近似解给出的波浪中心线对静水面的超高(Hz)中只涉及波高(H)和波长(L)，水深(d)是已知的，见下式：

(1)

图1的波浪超高示意图可给出浪高η和波高H的关系，包含的未知量为浪高η、波高H和波长L.

(2)

图1 波浪超高示意图

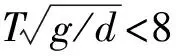
(3)

表演水池蓄水后水平面距池壁顶端0.3 m，一般情况下表演中虎鲸跳跃激起的波浪碰撞池壁的雍高部分会溢出池外，但单纯的浪高部分不会溢出池外.因此，假定浪高η为基本变化量，分别取浪高为0.30、0.25、0.20、0.15、0.10 m.联立式(1)、(2)、(3)求得波长、波高和周期，列入表1中.

表1 各个浪高的波浪三要素值

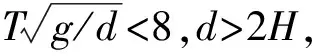
2 规范方法计算动水压力

确定了鲸鱼表演涌浪的波浪三要素以后，可根据《海港水文规范》(JTS 145-2—2013)和《水工建筑物荷载设计规范》(DL 5077—1997)计算波浪对直立亚克力板的动水压力.表2中列出了不同浪高下，鲸鱼表演涌浪的基本参数.其中Hcr为波浪破碎时的临界水深.

如表2所示，动物表演涌浪满足H/L≤1/30，d≥Hcr，d/L>0.5，符合《海港水文规范》8.1.4 条和《水工建筑物荷载设计规范》14.2.1条规定的应用条件.根据规范分别计算出的动水压力分布图如图2、3所示.图中假定在水面以上一个波高处动水压力降为零.因为表演水池波浪与河道中的波浪相比很小，《水工建筑物荷载设计规范》求解波浪中心线至计算水面高度的公式并不适用于表演水池波浪，所以把波浪中心线至计算水面高度的计算公式改为式(1).

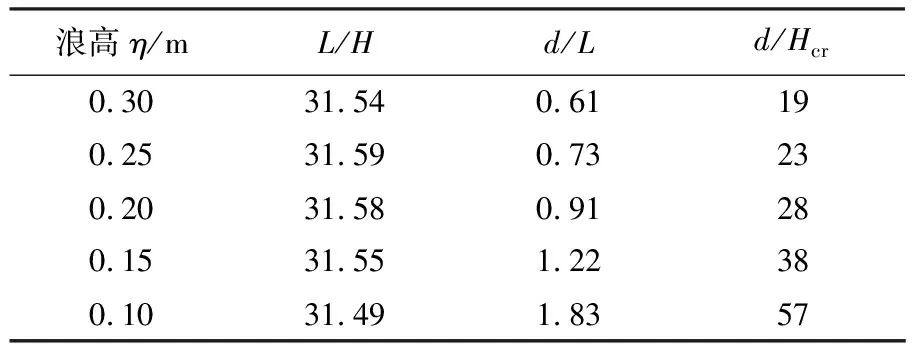
表2 涌浪基本参数

图2 《海港水文规范》波峰动水压力分布图

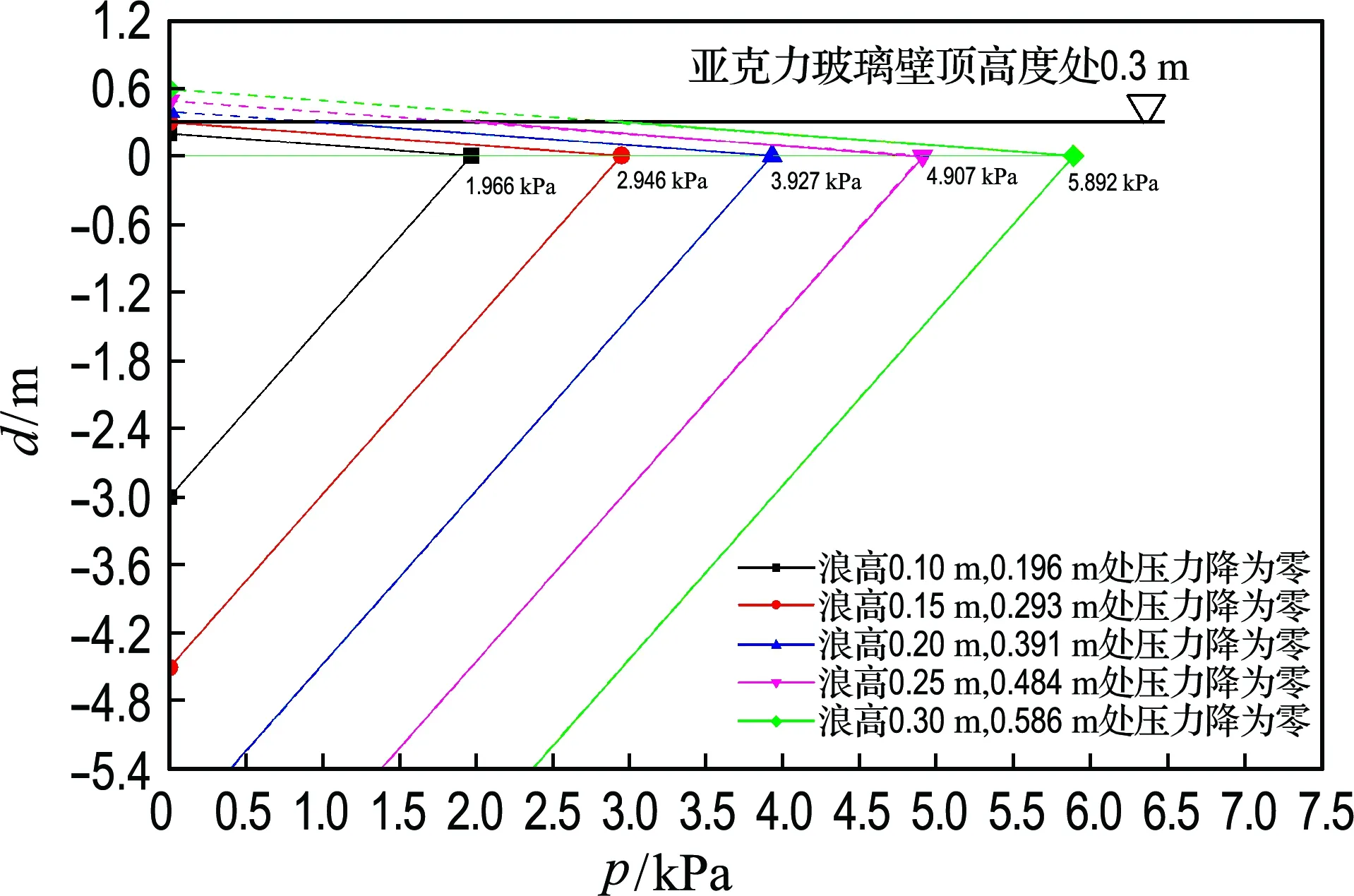
图3 《水工建筑物荷载设计规范》波峰动水压力分布图

Fig.3 Hydrodynamic pressure distribution diagram under the wave crest of Specifications for Load Design of Hydraulic Structures

对比两种规范计算出的动水压力分布线可以看到：在各个浪高下，水平面附近二者的压力值大小比较接近；水平面以下部分《水工建筑物荷载设计规范》计算出的动水压力比《海港水文规范》大，《水工建筑物荷载设计规范》动水压力在水面以下呈直线分布，《海港水文规范》动水压力在水面以下呈曲线分布.

3 模型试验

为了进一步研究亚克力板在涌浪作用下的动水压力和变形，进行了虎鲸跳跃入水产生涌浪的缩尺模型试验.

3.1 模型比尺及测试仪器

缩尺模型按照1∶15的比尺进行设计.试验中选长、短各一块亚克力板，在其中部安装压力传感器测量动水压力，安装百分表测量最大位移，图4还示出了浪高仪的安装位置.1号板上压力传感器的安装位置见图5.浪高仪和压力传感器的采集频率为512 Hz，系统误差小于±2%.

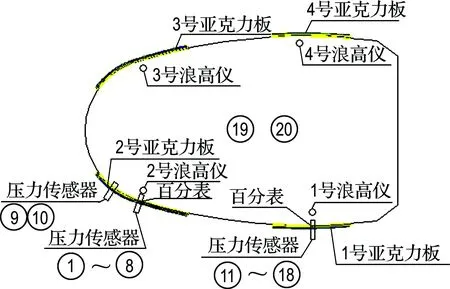
图4 表演水池模型及仪器布置平面图

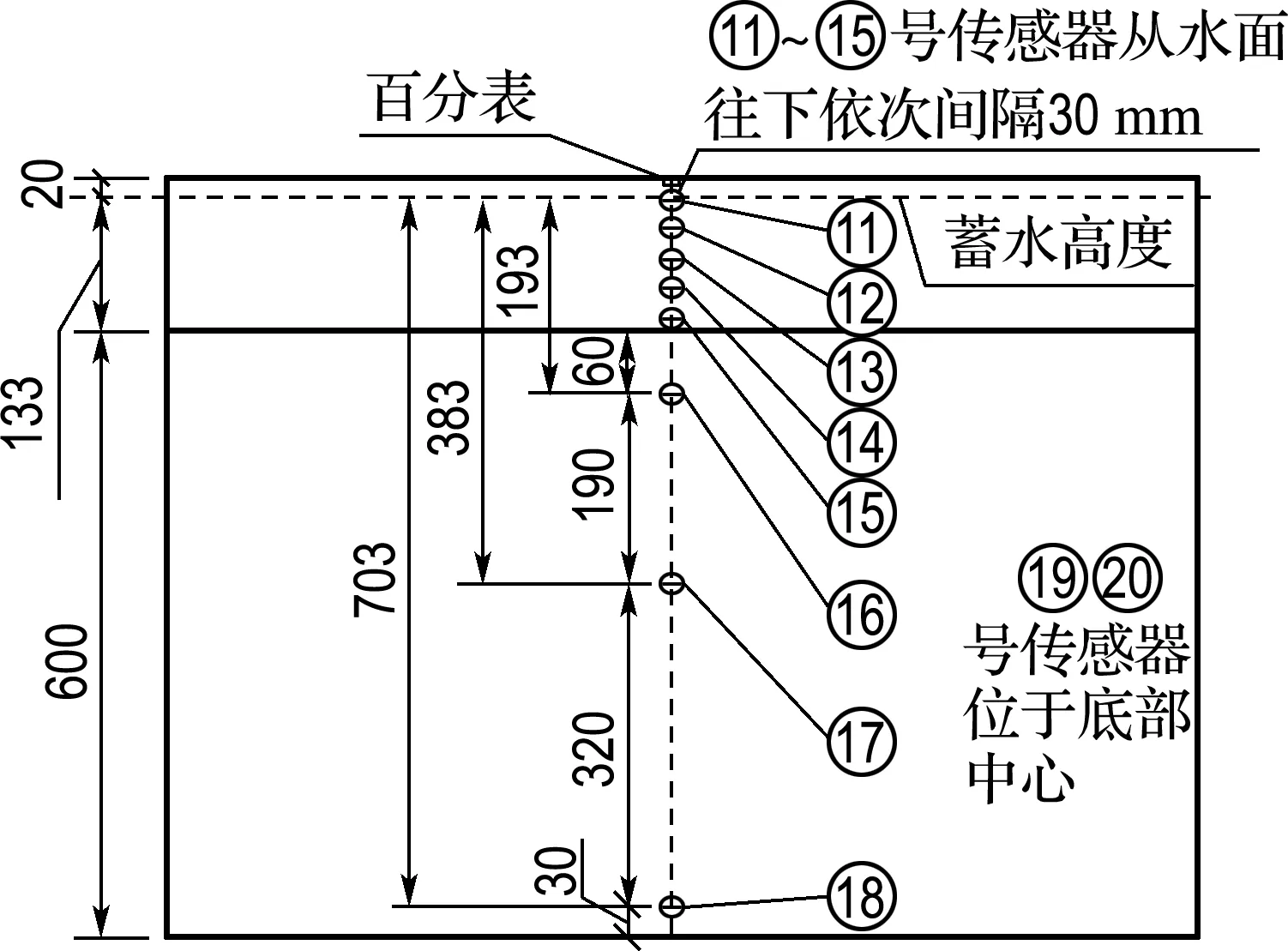
图5 1号亚克力板传感器布设图(单位:mm)

3.2 模型相似

原型、模型相似设计的原则是表演水池池水的重力相似和池壁的弹性相似，采用弹性力-重力相似律[14-15].模型试验中各物理量比尺列入表3中.

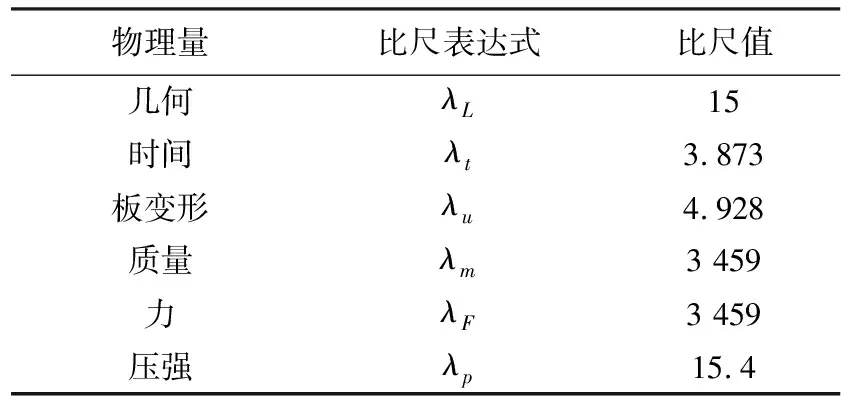
表3 各个物理量的比尺

3.3 试验方案

实际表演水池中最多有4条虎鲸同时表演，虎鲸重达6 t，最大可跃出水面5 m.模型鱼的选择应保证质量和体积相似，还要考虑其入水姿态的灵活性.因此，选择价廉的草鱼，质量在1.73 kg左右.虽然草鱼与虎鲸体型有所差异，但其相对密度接近，质量相似，有较好的入水姿态，模拟动水压力较好.若采用人工制造的假鱼为模型鱼，则相对密度接近1.0且耐水的材料较难选择，加工后还需要人工配置重块，模型鱼的重心平衡难以控制，且不能调整入水姿态，影响动水压力的数值与分布.鱼的筛选条件是外形、质量以及尺寸3个方面，由于虎鲸特殊的体形，头部浑圆、体形偏胖，寻遍各种鱼类，只有比较胖的草鱼相对较好.为了模拟实际表演中的虎鲸入水情形，要求草鱼抛掷轨迹线的最高点距水面330 mm，鱼头斜向入水，草鱼入水点要距离浪高仪300 mm以上，以免影响测量精度.

根据虎鲸表演进行了4种工况的试验.工况1，只有1条虎鲸跳跃入水；工况2，同时有2条虎鲸跳跃入水；工况3，同时有3条虎鲸跳跃入水；工况4，同时有4条虎鲸跳跃入水.

试验中发现，入水点至测量仪器距离对涌浪和动水压力的影响最大.

3.4 实测动水压力结果

将各工况下模型试验中鱼跃涌浪产生的最大动水压力换算到原型，求出设计方案中虎鲸表演产生的最大动荷载.图6为4种工况下，根据模型试验求出的虎鲸鱼跃涌浪的最大峰值压力.可以看出4种工况下，位于水面以下的峰值压力均随水深增加而减小，且呈现曲线分布.水面以上没有测点，因此假设在水面以上一个波高处的动水压力降为零.整理4种工况压力线得到沿水深变化的动水压力峰值包络线，如图6所示.其中，包络线-1.8 m以上的部分和工况1压力线重合，-1.8 m以下的部分和工况4压力线重合.

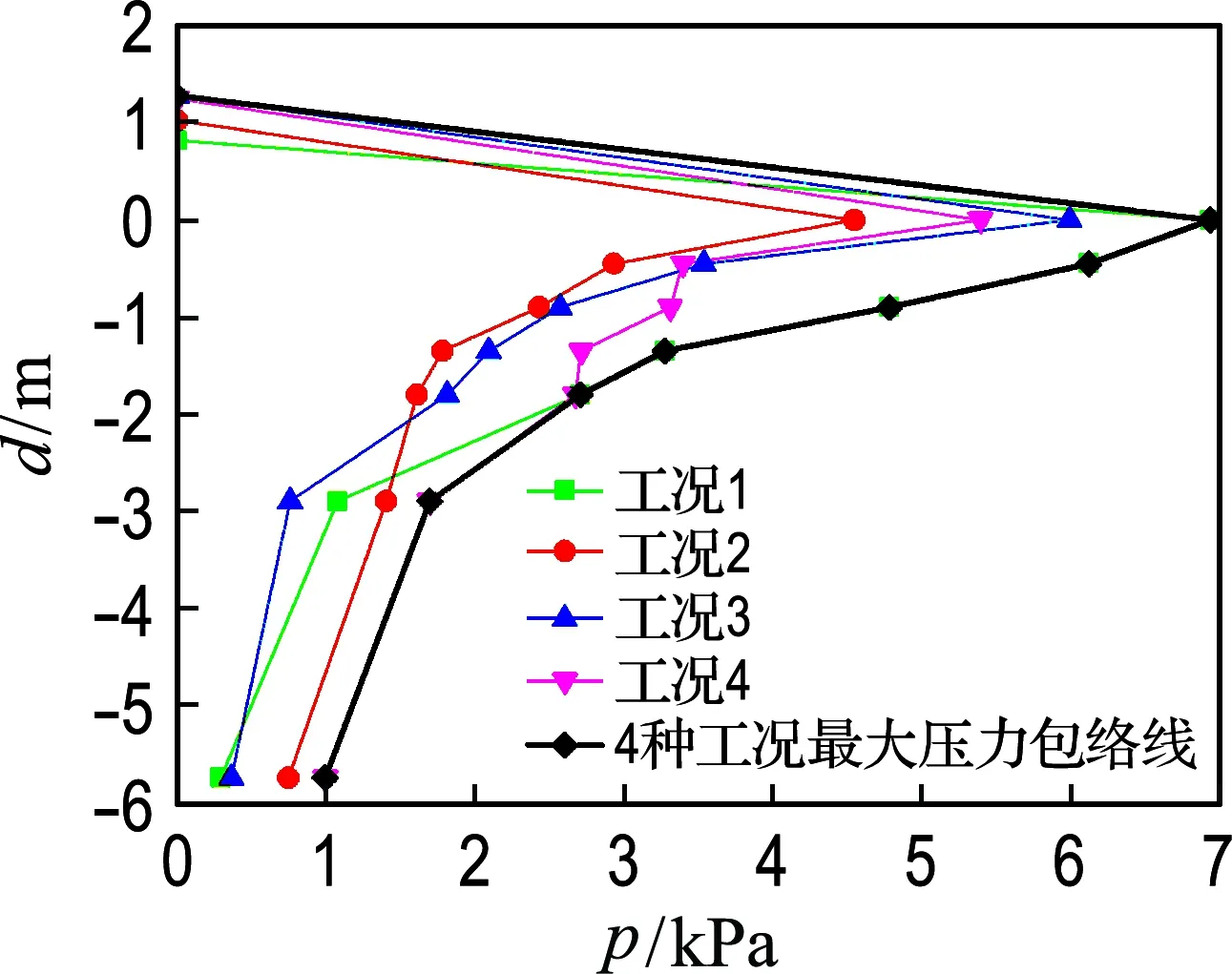
图6 4种危险抛鱼情况波峰时最大压力包络线图

Fig.6 Maximum pressure envelope diagram of four kinds of dangerous throwing fish

将试验动水压力包络线和两个规范计算出的动水压力分布线做对比，对比图见图7.其中，规范计算的动水压力分布线都是浪高0.30 m情况下的.如图所示，水面线以上《水工建筑物荷载设计规范》和《海港水文规范》的动水压力线几乎重合为一条直线，并且小于试验包络线.水面线以下，《水工建筑物荷载设计规范》动水压力线呈直线分布，《海港水文规范》动水压力线呈曲线分布.当水深小于-0.67 m时，试验值高于规范动水压力；当水深大于-0.67 m时，《海港水文规范》动水压力线和试验包络线基本吻合，并且小于《水工建筑物荷载设计规范》动水压力线.

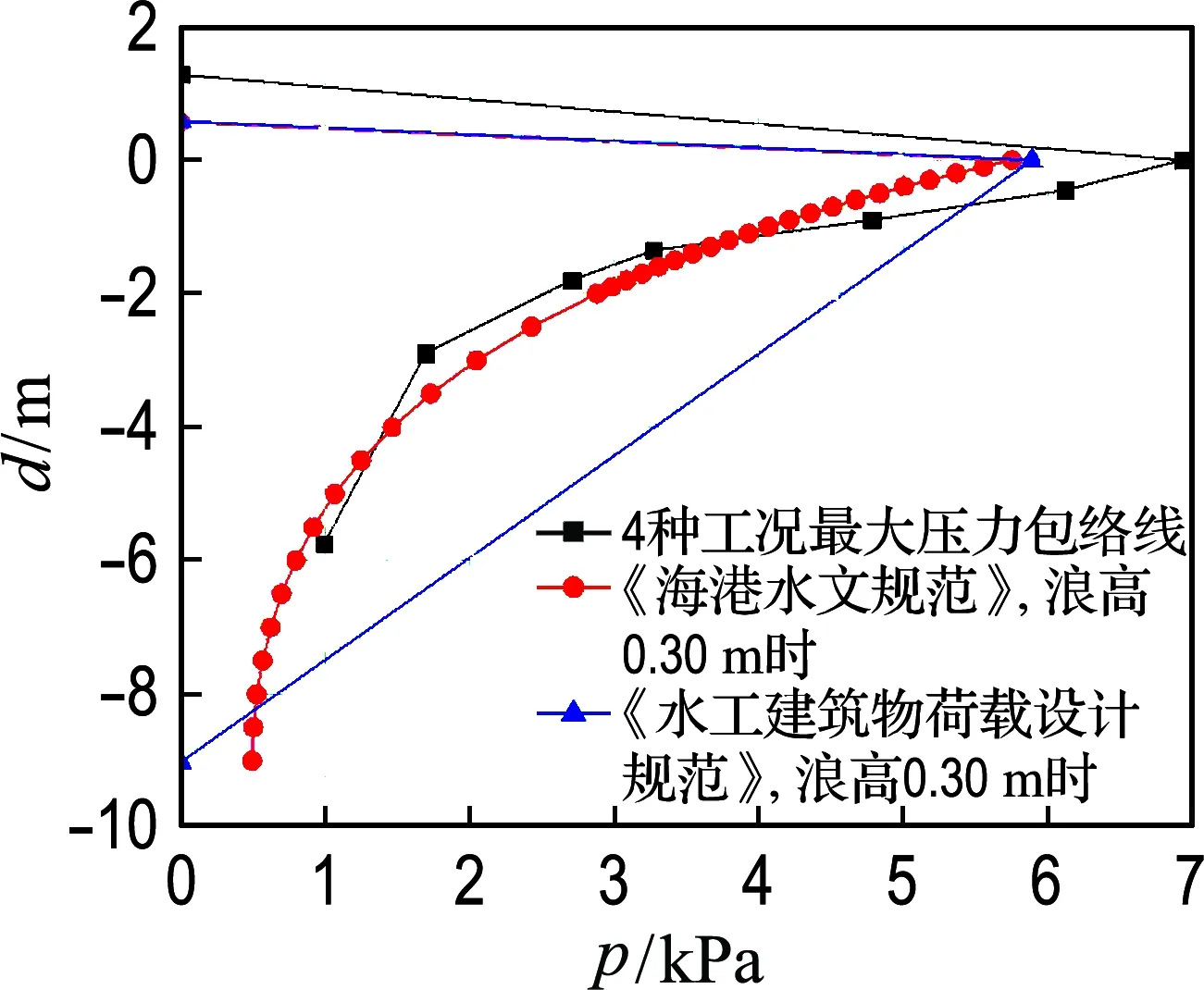
图7 试验波浪压力峰值包络线及规范分布线

总体而言，试验测定的动水压力和《海港水文规范》计算得到的动水压力在大小和分布上比较一致.这表明：可以采用《海港水文规范》准确计算动物表演涌浪动水压力；用基于波浪理论给出的虎鲸表演涌浪三要素来计算动水压力的方法经过试验证明是可行的，同时也验证了虎鲸表演涌浪三要素计算的合理性.

进一步分析，《水工建筑物荷载设计规范》浪压力计算方法是通过水工试验得到的，仅适用于风浪对坝、水闸等挡水建筑物(不包括海堤、河堤)，主要针对大风大浪对大坝的影响，较小的波浪并不适用.《海港水文规范》浪压力计算方法是通过统计的方法得到的，适用于海堤、河堤和防波堤等.通过图7的对比可以发现《海港水文规范》计算的结果和试验结果更相近，所以虎鲸表演落水形成的涌浪宜借助海港范畴的波浪来计算.

模型试验进行了多次蓄水和放水，测量得到静水压力作用下亚克力板的变形范围为5.963～9.856 mm.实测表演水池中1号亚克力板在动水压力作用下，工况2最大向外位移为4.192 mm.

4 数值模拟

将实测的动水压力时程换算成原型量值直接作用于表演水池的侧墙上，进行有限元数值模拟.由于表演水池由混凝土和亚克力板组成，其受力变形在弹性范围内，故均按弹性考虑，选用ANSYS 大型有限元分析软件进行模拟.

4.1 计算过程

有限元计算模型的模拟范围为亚克力板及以下墙体，两侧混凝土各延伸6 m，模型见图8，亚克力板截面尺寸见图9，亚克力板长13.876 m.混凝土墙体两侧和底边用全约束固定.混凝土与亚克力板之间底部采用竖向链杆连接，侧面采用面面接触连接.混凝土和亚克力板采用六面体立方体单元，尺寸分别为0.4 m和0.1 m.整个模型共分为14 500 个单元，17 790个节点.混凝土弹性模量为32.5 GPa，泊松比为0.2，密度为2 400 kg/m3；亚克力板弹性模量为2.942 GPa，泊松比为0.3，密度为1 200 kg/m3.

图8 1号亚克力板有限元计算模型

图9 亚克力板剖面图

荷载包括静水压力和涌浪产生的动水压力.沿水深动水压力的时程见图10.

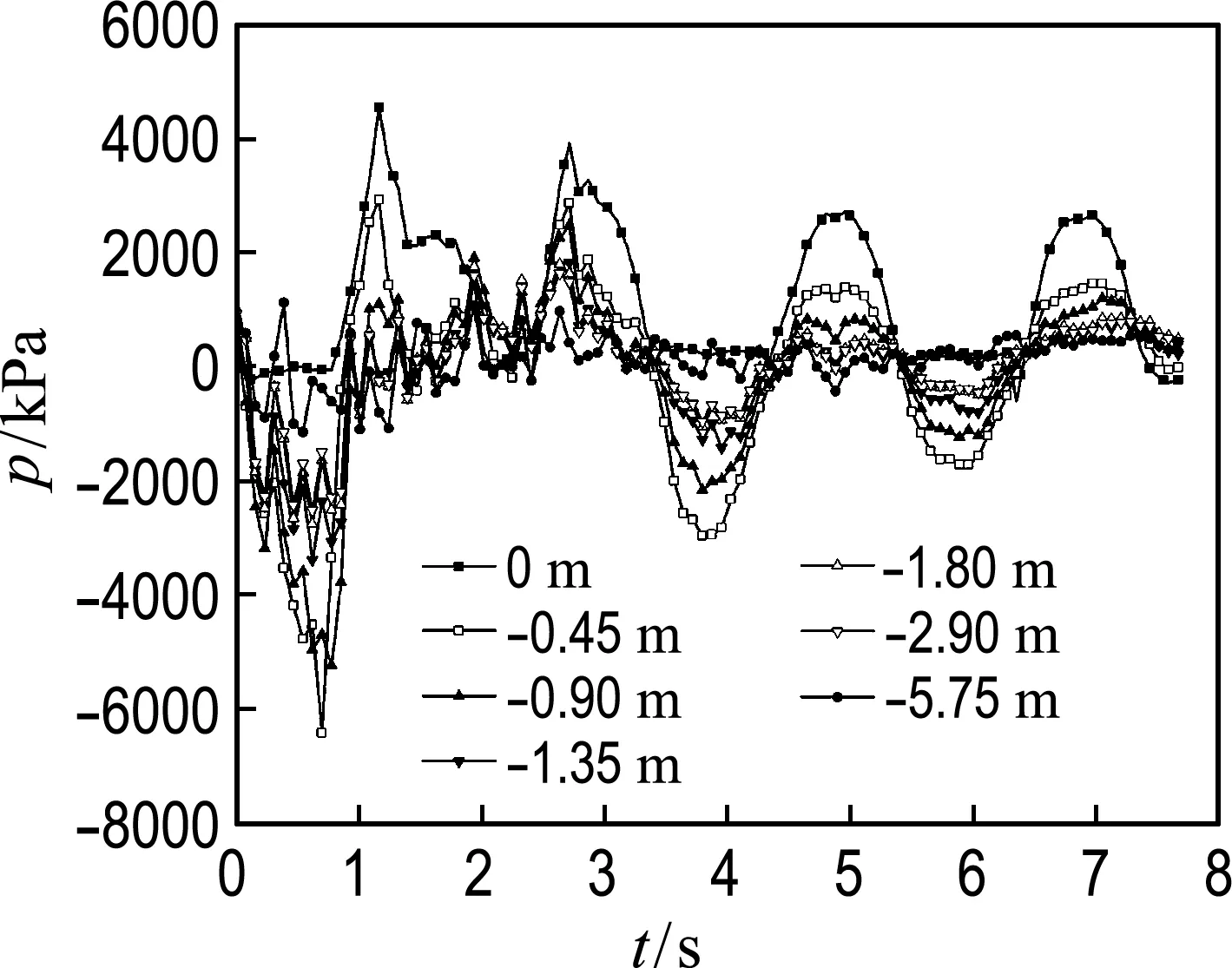
图10 工况2各水深压力时程曲线

4.2 计算结果

图11为静水压力下亚克力板及周围墙体变形图，在静水压力下亚克力板顶相对于板底位移为9.355 mm，和试验测量亚克力板变形范围5.963～9.856 mm基本符合.

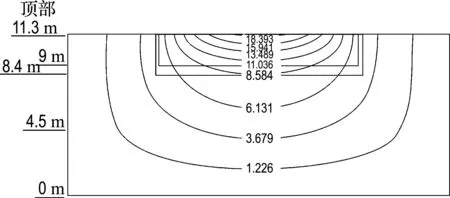
图11 有限元模拟静水压力下亚克力板变形等值线图(单位:mm)

Fig.11 Deformation contour map of acrylic plate under hydrostatic pressure by finite element simulation (unit:mm)

图12是工况2的动水压力作用下亚克力板最大变形图.在动水压力下亚克力板顶相对于板底的最大位移为5.285 mm.图13是工况2的亚克力板跨中顶点相对于跨中底部点的位移变形曲线，可给出最大向外位移(图中最大负值)同为5.285 mm，发生在最大压力时刻，其后各个时刻位移变形值随压力逐渐减小.模拟值5.285 mm比试验最大值4.192 mm大了1.093 mm.

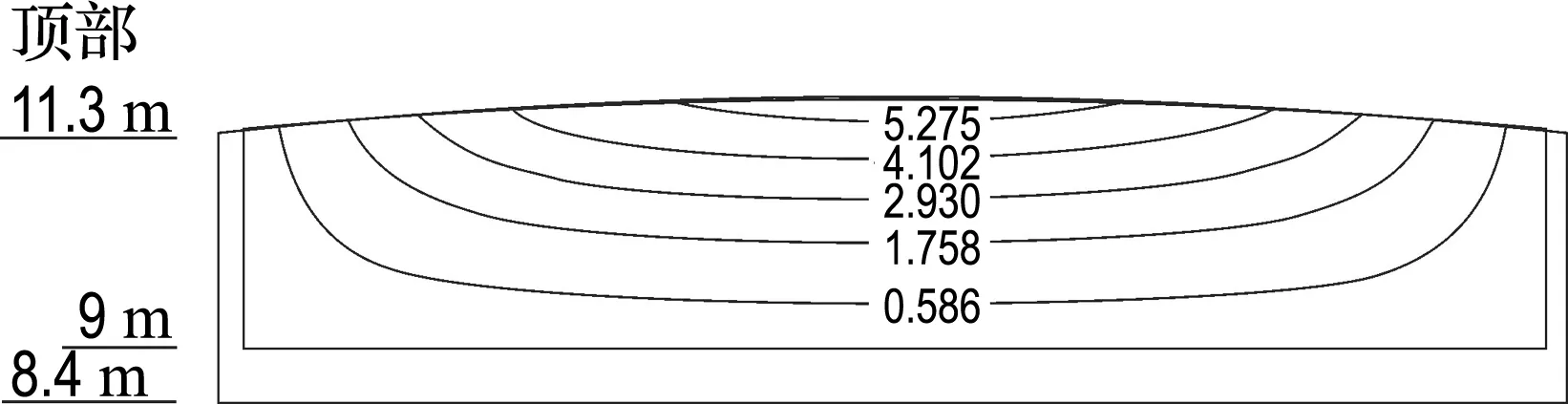
图12 有限元模拟动水压力下亚克力板变形等值线图(单位:mm)

Fig.12 Deformation contour map of acrylic plate under hydrodynamic pressure by finite element simulation (unit:mm)

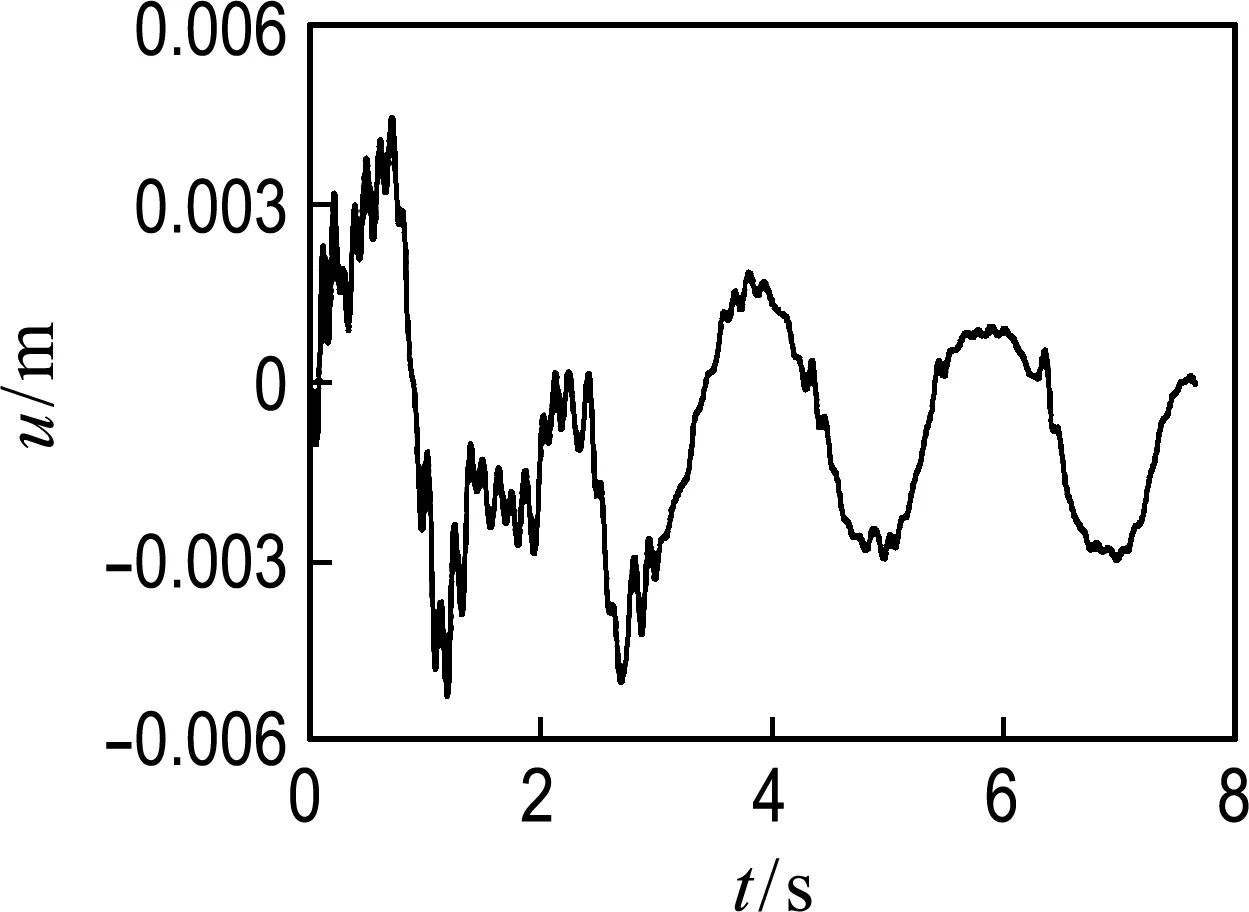
图13 亚克力板动水压力变形曲线

通过模型试验和数值模拟中的动力时程作用分析发现，最危险的时刻发生在第1列波峰时，随后位移逐渐减小.

5 讨论

表演水池亚克力板高2.3 m，约占整个表演水池深度的20%.虎鲸表演形成的动水压力虽然不大，缩尺试验得到的最大动水压力为7 kPa，但其分布容易使亚克力板变形.静水压力作用于水面以下，合力作用点偏下；而动水压力在水面处取得最大，往下衰减也较快，但其作用点在水面附近.因此，虎鲸表演形成的动水压力作用使类似悬臂梁结构的亚克力板较易向外变形.

试验和数值模拟结果表明，施加静水压力时，试验和模拟中板顶位移最小值为5.963 mm，施加动水压力时，试验和模拟中板顶位移最大值为5.285 mm，二者很接近，动水压力产生的位移是静水压力位移的88.6%.施加静水压力时，板顶最大位移为9.856 mm，施加动水压力时，板顶最小位移为2.809 mm，动水压力产生的位移是静水压力位移的28.5%.可以认为动水压力位移和静水压力位移属同量级.