柱式抗风浪环境监测浮标水动力特性研究

2018-07-23潘昀，左孝，冯德军，张清靖，桂福坤*

大连理工大学学报 2018年4期

潘昀，左孝，冯德军，张清靖，桂福坤*

(1.浙江海洋大学浙江省海洋养殖装备与工程技术重点实验室，浙江舟山 316022；2.北京市水产科学研究所渔业生物技术北京市重点实验室，北京 100068 )

0 引言

海洋资料浮标是一种布放在特定海域用于定点观测海洋环境的技术装备，能够长期、连续、自动地采集和发送海洋环境观测资料，是现代海洋环境立体观测系统的重要组成部分[1].20世纪60年代我国开始海洋资料浮标的研发，自主设计生产了多种结构形式的锚泊海洋资料浮标和专用海洋浮标[2]，浮标研制和测量技术已接近或达到世界先进水平.常见的浮标结构有圆盘形、船形和球形等，主要用于海洋水文气象资料的获取.但对专用于海洋养殖浮标的研究仍处在摸索阶段[3-4].

海洋设施养殖需要对不同深度水质情况进行监测，进而对养殖环境作出预警和调控.柱式浮标由桂福坤等[5]提出，主要由舱体、浮架、配重和锚绳等组成，浮架不同深度装有水泵抽取水样，可同时观测水面附近和水下剖面的环境参数，主要用于海洋养殖区.通过分析柱式浮标采集的环境数据，可对渔业投饵、鱼类健康等作出科学判断[6].与传统球形、圆盘形、船形浮标相比，柱式浮标与水体接触面积显著减小，降低了波浪对浮标的作用荷载，提高了浮标的抗风浪性能；柱式浮标整体重心在水下约10 m处，大大增加了其稳定性；不同水深处取水管道可以依附柱式浮标的圆柱，实现25 m水深分层取样监测水质数据.柱式浮标结构形式与传统浮标存在较大差异，因此需要探究波浪作用下柱式浮标的水动力特性，得到柱式浮标及其锚绳的波浪作用机制，分析其抗风浪性能，论证其能否适应复杂海洋动力环境，并提高数据采集准确度，这对海洋渔业生产有重要意义[7].

国内外学者已经做了较多关于浮标水动力特性的研究，Ryu等[8-9]应用完全耦合的时域方法计算了深水浮标的运动响应，并得到试验验证；Salem 等[10]采用线性化方法求解了运动方程，研究了CALM(catenary anchor leg mooring)浮标纵摇方向的运动响应；Monroy等[11]则应用SWENSE(spectral wave explicit Navier-Stokes equations)方法创建了新的波浪模型，研究CALM浮标在规则和不规则波下的运动响应；Chang等[12]研究了波浪作用下锚泊浮标的非线性动力响应，并构建了动态响应模型；张继明等[13]建立了频域内的运动微分方程，仿真了浮标模型在波浪中的运动，并利用模型试验对模型阻尼矩阵进行了修正；Zhu等[14]针对一球形锚泊浮标系统使用锚绳上的局部坐标系，构建了一种计算速度快、精度高的数值模型，分析了浮标时域和频域内的运动响应；何大华等[15]对较大误差下浮标倾角的测量方法进行了研究，给出了一种矩阵变换求解浮标姿态的方法.

上述研究都是针对传统浮标，尚无关于柱式浮标水动力研究及其在实际海域抗风浪能力验证研究.因此，本文基于上述关于浮标水动力特性研究的方法和内容，采用物理模型试验方法，研究柱式浮标在波浪条件下水动力特性，重点分析其运动姿态及锚绳拉力，为柱式浮标设计和抗风浪性能评估提供参考，并为后续数值模拟提供验证资料.

1 试验材料与方法

1.1 试验模型

试验在浙江海洋大学水动力实验室进行，试验水池尺度115 m×6.5 m×3.5 m，最大造波30 cm，周期0.5～2.0 s.试验中用到的仪器包括浪高仪(BG-100型，精度±1 mm，天津奥菱工业自动化科技有限公司)、拉力传感器(JLBS-P1型，满量程精度0.1%，蚌埠传感器系统工程有限公司)、数据采集系统等.浮标模型依据几何相似准则，按1∶7.8的比尺采用PVC管制作，如图1所示.受试验条件限制，PVC浮架质量大于原型重力缩小后的质量，所以以PVC浮架质量为参照标准，对照原型各部分质量比值设计舱体和配重的质量[16].

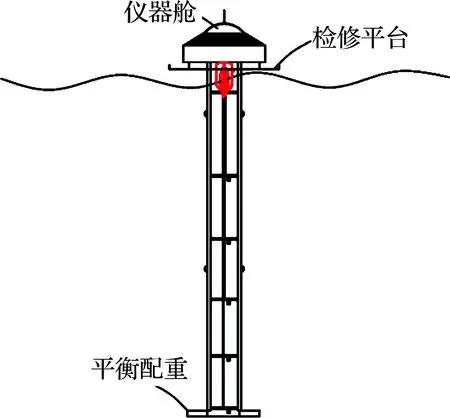
(a) 浮标结构示意图

(b) 浮标模型图

1.2 试验条件

谢冬梅等[17]统计了我国东海近海的平均有效波高为1.3 m(物理模型16.7 cm)，5%累积频率有效波高为3.0 m(物理模型38.5 cm)，波浪周期为1～5 s，结合浮标模型几何比尺和水池造波能力，采用两种工况进行试验条件的设计.

工况1：固定波浪周期2.0 s，5组波高(10、14、18、22、26 cm)，尽量选择较大波高的波浪研究浮标模型水动力特性变化，探究浮标抗风浪性能.

工况2：固定波高18 cm，5组波浪周期(1.6、1.8、2.0、2.2、2.4 s)，尽量选择较多组次的波浪周期研究浮标模型水动力特性变化，探究浮标稳定性.

如图2所示，两两锚绳呈120°系缚浮标模型，固定于水池中央，迎波面锚绳为B锚绳，两侧为A锚绳和C锚绳，3根锚绳的固定端连接拉力传感器.在B锚绳与拖车系缚点布置1支浪高仪，与拉力传感器一并连接到数据采集系统，实现波高和拉力的同步采集.浮标正下方布置CCD图像采集系统，使用同一台电脑进行操作采集，形成集浮标运动、锚绳拉力、浪高为一体的采集装置.试验设备和各项参数调试完成后，启动造波机按照工况1和工况2进行造波，同步采集波高和锚绳拉力数据，并使用CCD摄像机采集浮标模型上两个发光二极管的运动轨迹(图1(b)).

1.3 数据采集与处理

1.3.1 CCD图像采集试验开始前调试二极管，保证其正常工作，提供稳定光源.待水池形成稳定波浪后(经过浮标约3个波浪，此时水池后端仍未形成波浪，无波浪的二次反射影响)，采集拉力的同时，打开CCD摄像机，连续采集180张8位灰度图像.灰度图像上两个发光点即为浮标上端二极管瞬时位置，通过自行开发的图片分析软件对灰度图像中光点跟踪分析处理得到浮标模型的运动轨迹[18].

图像处理软件通过对180张灰度图像中两个发光点的连续跟踪，得到图3(a)所示的示踪点运动轨迹.试验中轨迹采集时间为10 s，包括4～6个完整运动周期的轨迹，对图3(a)中几个完整周期内的轨迹做平均处理，得到的运动轨迹更清晰准确，减少试验误差，如图3(b)所示.

1.3.2 锚绳张力采集造波机启动后，待2～3个波浪经过浮标模型后，开始采集3根锚绳上拉力传感器的受力数据，每次持续采集10 s连续数据，采集完成后，统计分析浪高仪采得的波高数据，若满足预设波高条件的精度则保存数据，否则重新试验，直至满足试验精度.最终得到满足试验精度要求的3次重复试验，取拉力平均值作为对应波浪条件下的锚绳拉力.图4(a)为采集的拉力源数据，通过快速傅里叶变换算法，对数据进行毛刺处理.快速傅里叶变换是离散傅里叶变换的高效算法，在图像信号处理中得到广泛应用[19].图4(b)为滤波后的数据，经过处理，数据中毛刺明显减少的同时，保证了数据的客观性.

图2 试验示意图

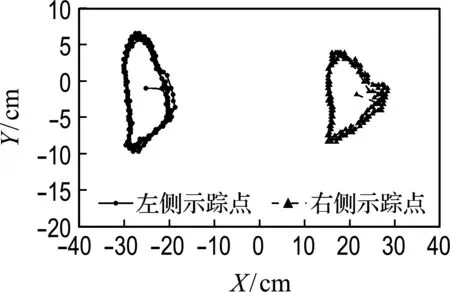
(a) 示踪点运动轨迹

(b) 平均后的示踪点运动轨迹

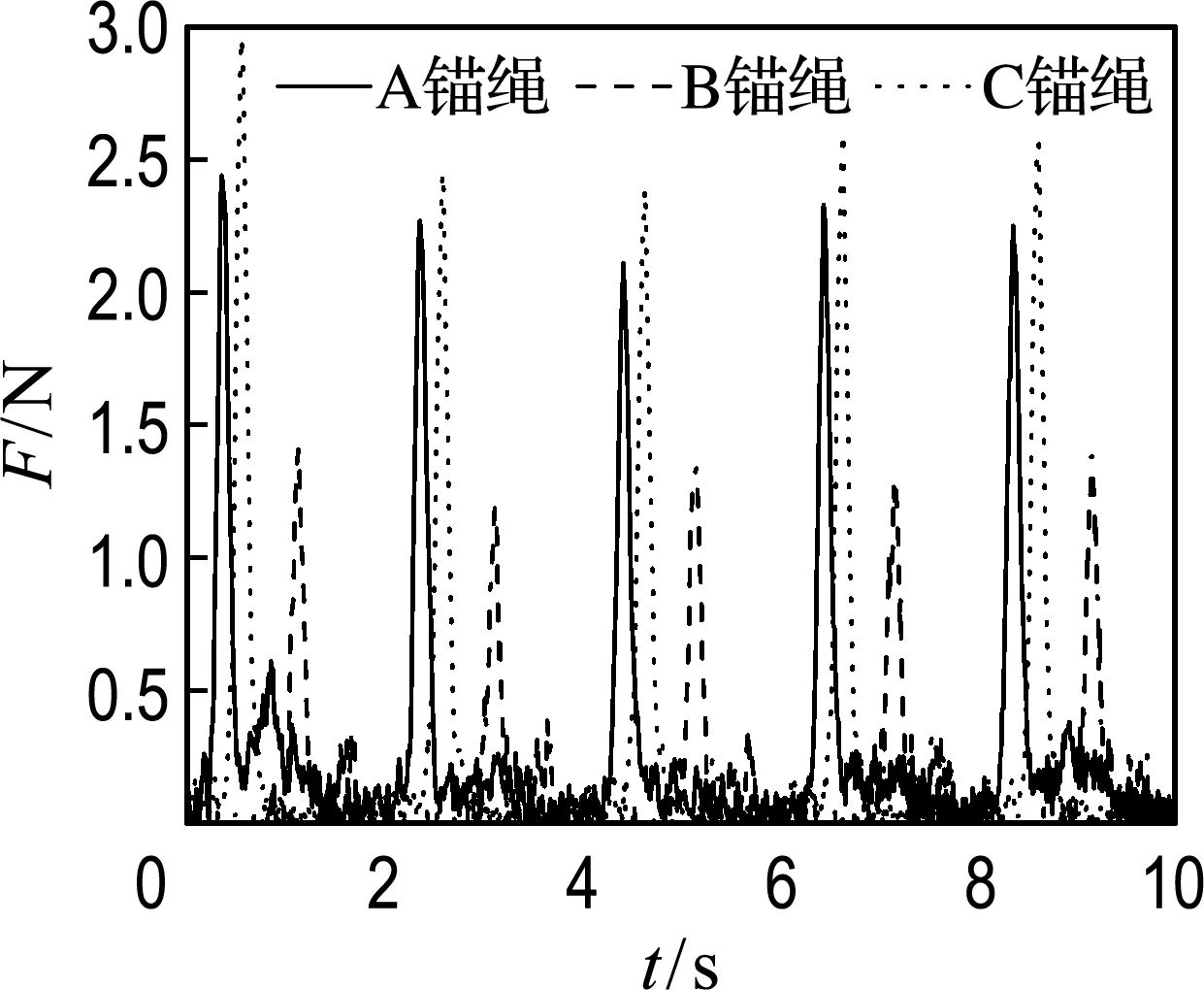
(a) 滤波前数据

(b) 滤波后数据

2 试验结果与分析

2.1 浮标运动轨迹分析

图5(a)、(b)分别为左、右侧示踪点在固定周期为2.0 s，波高分别为10、14、18、22、26 cm的5种条件下的运动轨迹.取水面静止时两示踪点位置的中点为坐标原点，可以得出，总体上浮标的运动轨迹呈近似的椭圆形.随着波高增大，两侧示踪点运动轨迹的右端均向X轴正方向增大，运动轨迹的左端几乎保持不变，Y轴正负方向均有所增大.随着波高增大，在B锚绳系缚点的作用下，运动轨迹呈右移的趋势，轨迹越来越“扁平”.

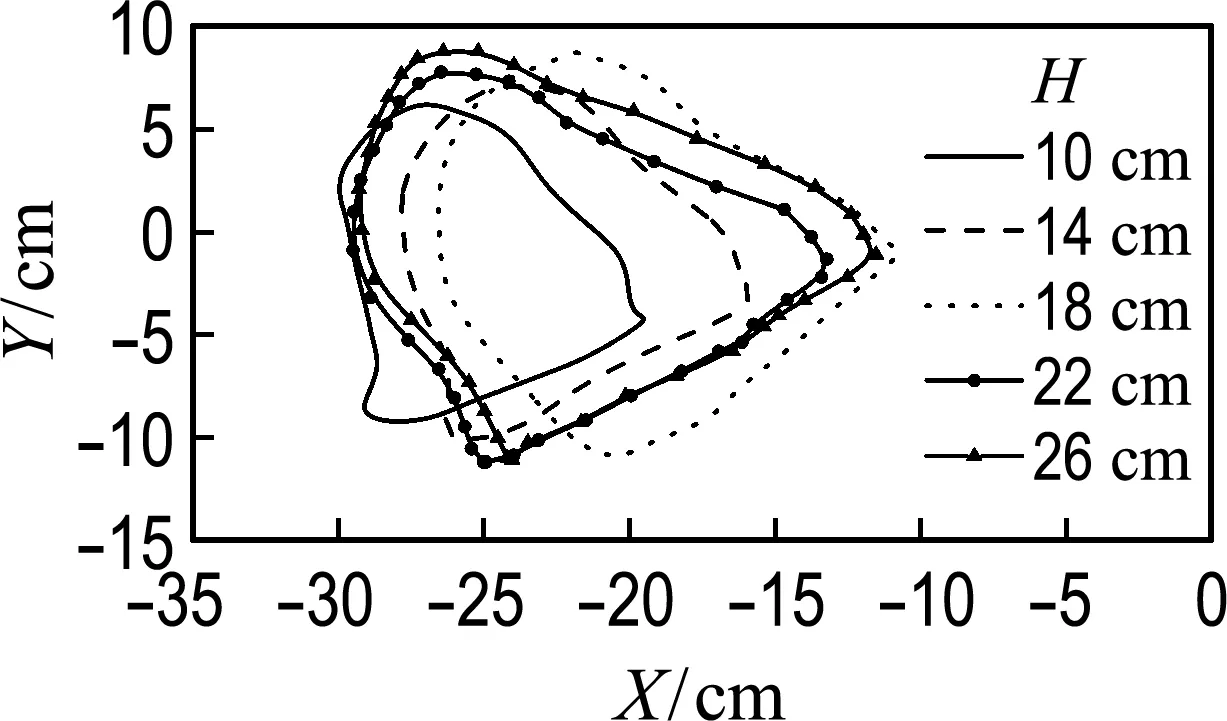
(a) 左侧示踪点运动轨迹

(b) 右侧示踪点运动轨迹

图5 示踪点运动轨迹(工况1)

Fig.5 Tracing point trajectory (Case 1)

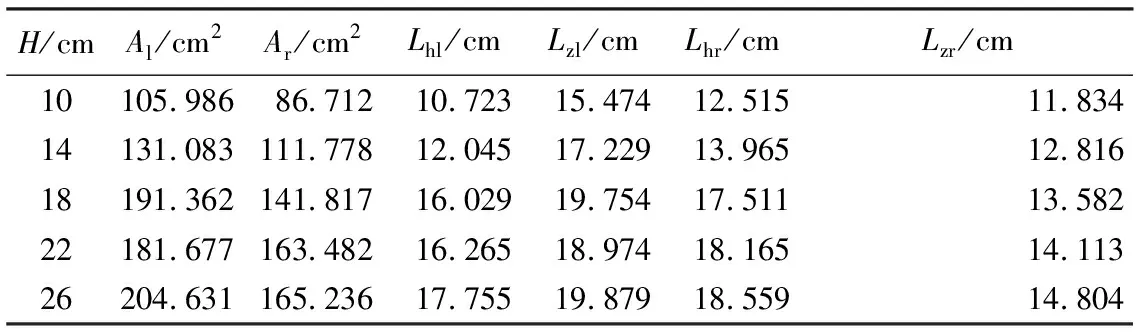
表1 示踪点运动轨迹的特征值(工况1)

表1给出了浮标模型示踪点运动轨迹随波高变化的特征值，其中Al、Ar分别表示左、右侧示踪点运动轨迹面积，Lhl、Lhr分别表示左、右侧横摇幅度，Lzl、Lzr分别表示左、右侧纵摇幅度.由表1可见，随着波高增大，总体上运动轨迹包含的面积是不断增大的，反映了浮标运动在加强.同时，左侧示踪点对应的运动轨迹面积大于右侧示踪点，说明左侧示踪点的变化更大，但当波高增大至22 cm后，运动轨迹面积变化较小.随着波高增大，浮标横摇幅度也增大，而且其两侧示踪点的运动规律基本一致，均在10 cm到18 cm波高横摇幅度显著增大，在波高达到22 cm后，增大减缓.最小波高到最大波高，左、右两侧横摇幅度分别增大了7 cm和6 cm.随着波高增大，浮标纵摇幅度也增大，其中左侧示踪点表现更为剧烈，增大了4.4 cm，而右侧示踪点为3.0 cm，但波高为22 cm时左侧示踪点甚至出现减小.

图6(a)、(b)分别为左、右侧示踪点在固定波高18 cm，周期分别为1.6、1.8、2.0、2.2、2.4 s的5种条件下的运动轨迹.取水面静止时两示踪点位置的中点为坐标原点，随着波浪周期增大，左、右两侧示踪点运动轨迹的右端先向X轴正方向偏移，在周期2.2 s时迅速向X轴负方向偏移，运动轨迹的左端则几乎保持不变，运动轨迹在Y轴正负方向均有明显偏移.浮标的运动轨迹呈近似的椭圆形，随着波浪周期增大，在B锚绳系缚点的作用下，运动轨迹先向右偏移后向左偏移，轨迹也由原来的“扁平”向“狭长”转变.

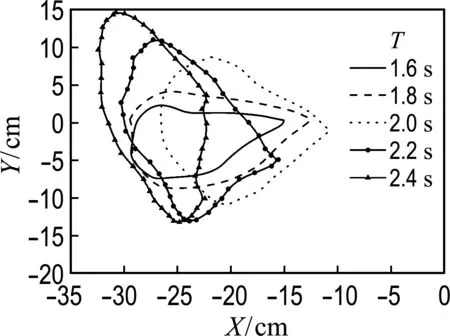
(a) 左侧示踪点运动轨迹

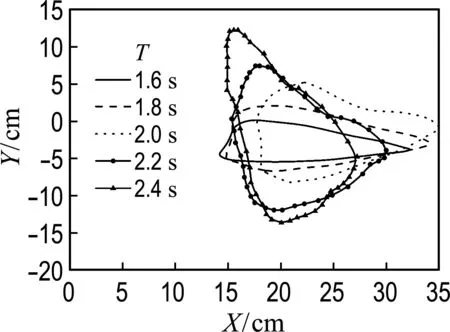
(b) 右侧示踪点运动轨迹

图6 示踪点运动轨迹(工况2)

Fig.6 Tracing point trajectory (Case 2)

表2给出了浮标模型示踪点运动轨迹随波浪周期变化的特征值.由表2可见，随着波浪周期增大，总体上运动轨迹包含的面积在不断增大，反映了浮标运动逐渐加强.其中，左侧示踪点运动轨迹面积并非持续增大，在周期为2.4 s时出现减小，右侧则表现为持续增大，并且左侧示踪点运动轨迹面积始终大于右侧.关于横摇幅度，两侧示踪点变化规律相近，均只在周期为1.8 s时增大，其后都在减小.右侧的横摇幅度整体大于左侧，且右侧横摇幅度最大差值约为7.3 cm，左侧横摇幅度最大差值约为7.0 cm.关于纵摇幅度，左、右两侧示踪点变化趋势几乎一致，随着波浪周期增大都大梯度增大，其中左侧示踪点的纵摇幅度大于右侧.数值上，左、右两侧的纵摇幅度均增大约20 cm.

表2 示踪点运动轨迹的特征值(工况2)

2.2 浮标摇摆角度分析

图7(a)为工况1中5个波高下浮标模型水平方向摇摆角度统计，以垂直向上方向为0°，水平向左为正，水平向右为负.统计图7(a)中每个波高对应的摇摆角度峰值和谷值，求平均值得到图7(b).如图所示，在固定周期2.0 s下，当波高增大到26 cm，其对应的摇摆角度比波高为10 cm时在正方向增大了约2.6°，在负方向增大了约2.2°.10～22 cm波高摇摆角度峰值近似在同一条水平线上，14～26 cm波高摇摆角度谷值近似在同一条水平线上，随着波高增大，浮标摇摆角度没有明显变化，说明浮标在波浪中的稳定性极好.

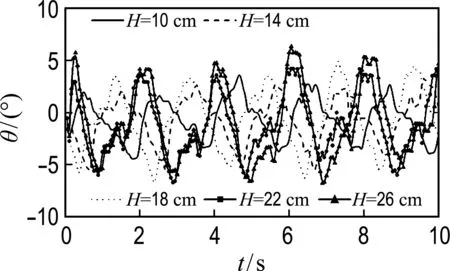
(a) 摇摆角度随时间的变化

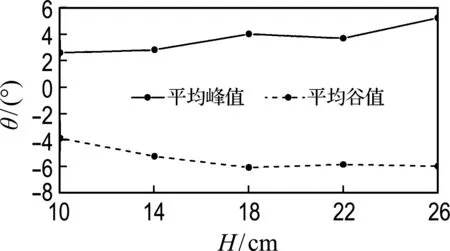
(b) 摇摆角度峰值和谷值随波高的变化

图7 摇摆角度的变化(工况1)

Fig.7 Changes of swing angle (Case 1)

图8(a)为工况2中5个周期下浮标模型水平方向摇摆角度统计.如图所示，在波高恒定18 cm下，随着周期增大，浮标摇摆角度整体变化不明显，并且各周期下浮标摇摆角度峰值和谷值差值几乎保持不变，最大约为10°，表明在锚绳的束缚作用下，浮标在水平方向摇摆程度几乎不变，受波浪周期影响，浮标整体会向负方向稍稍倾斜.

2.3 锚绳拉力分析

(a) 摇摆角度随时间的变化

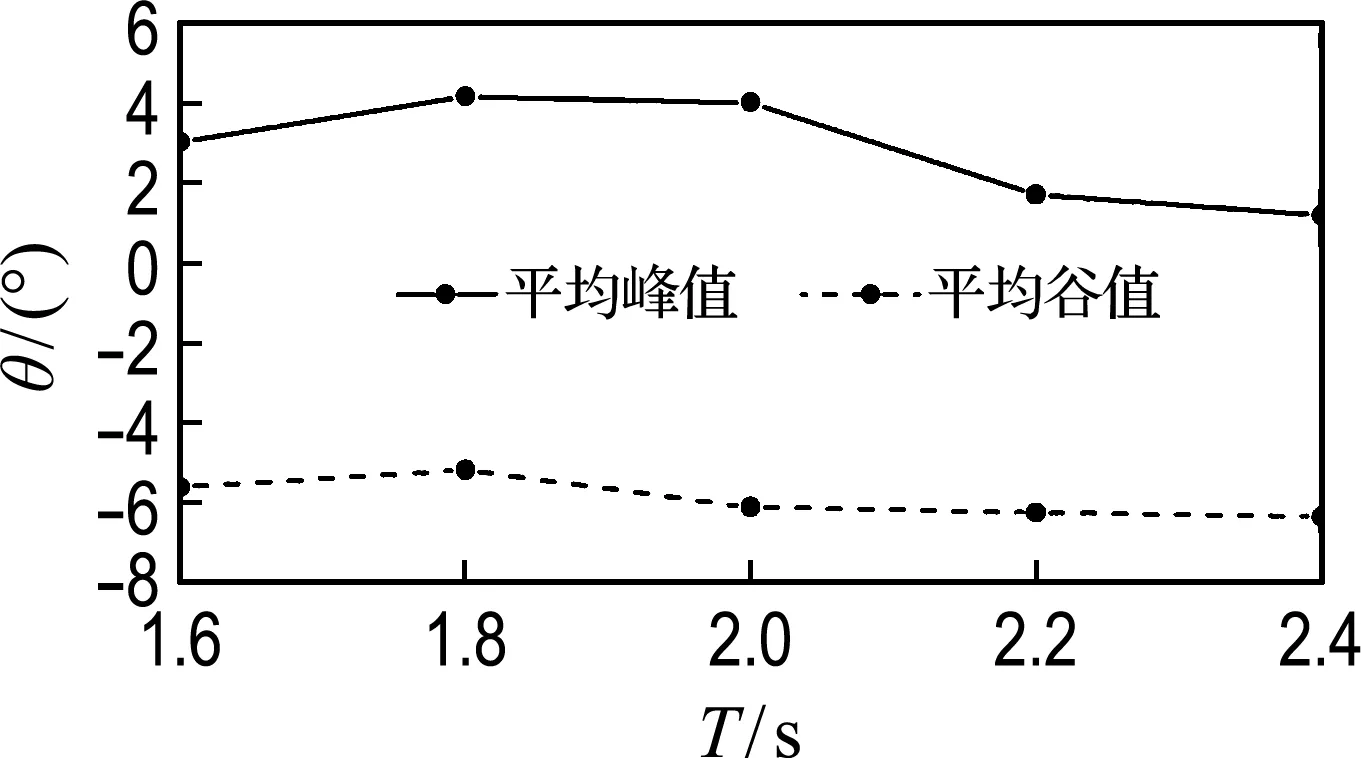
(b) 摇摆角度峰值和谷值随周期的变化

图8 摇摆角度的变化(工况2)

Fig.8 Changes of swing angle (Case 2)

图4(b)为A、B、C锚绳终端3个拉力传感器同步采集的锚绳平均拉力数据.A、C锚绳对称分布，所以拉力基本同步，但由于试验锚绳的布置和拉力传感器测量误差的原因，图4(b)中A、C锚绳拉力存在较小差异，这对分析浮标水动力特性规律并无影响.而B锚绳拉力明显小于A、C锚绳，且B锚绳拉力出现第二次峰值，这与图2中的锚泊方式有关.

采用特征值分析的方法，对锚绳进行受力分析.选取每种条件下锚绳拉力峰值的平均值作为对应锚绳的拉力特征值.如表3为波高10 cm、周期2.0 s的特征值统计结果.

表3 锚绳拉力的峰值

如图9分析波高和波浪周期对锚绳最大拉力的影响，不同的试验条件下，A、C锚绳的最大拉力变化规律相近.如图9(a)所示，随着波高从10 cm增大到26 cm，拉力明显增大，但可以看到，拉力增大的梯度在减小；B锚绳随着波高增大拉力几乎保持不变，不受波高影响.从锚绳拉力可以得出，柱式浮标对波高的抵抗效果非常明显.如图9(b)所示，随着周期增大，A、C锚绳拉力缓慢减小，最大差值仅为0.8 N，而B锚绳拉力逐渐减小.因此，柱式浮标锚绳拉力受周期影响较小.

(a) 锚绳拉力随波高的变化

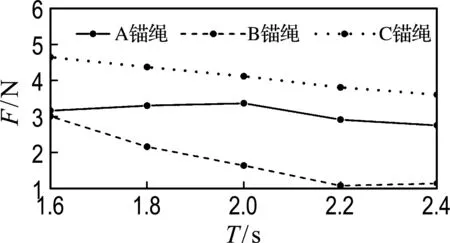
(b) 锚绳拉力随周期的变化

图9 两种工况下锚绳拉力的变化

Fig.9 Changes of anchor rope tension in two cases

3 讨论

本文试验中通过改变波浪要素研究柱式浮标的水动力特性以及三向锚绳系缚下锚绳拉力情况.浮标的运动轨迹与波浪要素直接相关，但右侧示踪点的运动轨迹在面积、纵摇幅度等方面始终小于左侧，仅横摇幅度大于左侧，这与试验中采用的三向锚绳系缚方式有关(见图2).由于右侧示踪点对应的B锚绳平行于波浪传播方向，从而浮标模型B锚绳系缚点的竖直方向束缚较大，运动轨迹呈现出水平方向运动.通过对浮标的摇摆角度分析发现，随着波高增大，摇摆角度变化最大不超过3°，且左、右两侧横摇幅度分别增大了约7 cm和6 cm，纵摇幅度分别增大了约4.4 cm和3.0 cm.波高对浮标横摇的影响比对浮标纵摇影响大，结合摇摆角度仅有3°的变化，进一步印证了柱式浮标对波高的抵抗能力十分优越.随着周期增大，摇摆角度在正负方向的差值几乎不变，也就是浮标在水平方向的摇摆幅度几乎不变，只是向一边有微小的偏移.摇摆幅度上，波高为18 cm时，左、右侧横摇最大差值分别为7.0 cm和7.3 cm，左、右侧纵摇均增大约20 cm.显然，周期对浮标纵摇的影响远大于对浮标横摇的影响.综上所述，柱式浮标对不同波高的波浪适应能力较强，能够保证一定的稳定性，确保精确取得目标水深的水样.柱式浮标的稳定性对波浪周期较敏感，大周期波浪会导致浮标在垂直方向上有较大幅值的升降.

定波浪周期(2.0 s)下，随着波高增大，浮标模型运动加强，锚绳拉力增大，但锚绳拉力增大的速度较缓.A、C锚绳拉力变化同步，规律相似，数值略有差异，最大差异为1.1 N.B锚绳拉力远小于A、C锚绳，而且其值大小受波高影响较小(<0.5 N).由于A、C锚绳拉力大于B锚绳拉力，导致图5(a)、(b)中轨迹线左半边运动明显强于右半边.借鉴冲量的概念，冲量I=Ft=mΔv，即动量变化量等于波浪力F与作用时间t的乘积，可以得出F=mΔv/t，在浮标质量不变的前提下，根据运动轨迹数据计算浮标在采样时间间隔内的平均速度v，得到最大波浪力如表4所示.此最大波浪力由运动轨迹数据间接计算得到，与拉力传感器实测的波浪力相比较，同样得到最大波浪力受波高影响较小的规律，进而得出迎波面锚绳(B锚绳)拉力与波浪作用下浮标动量变化量相关，而并不能仅以波高进行解释.试验中，波浪传播方向平行于B锚绳，受试验条件限制，并未进一步研究波浪传播方向对锚绳拉力的影响，可根据现有的试验结果和结论，针对实际海域中海流、波浪的运动规律调整布放浮标和锚绳.

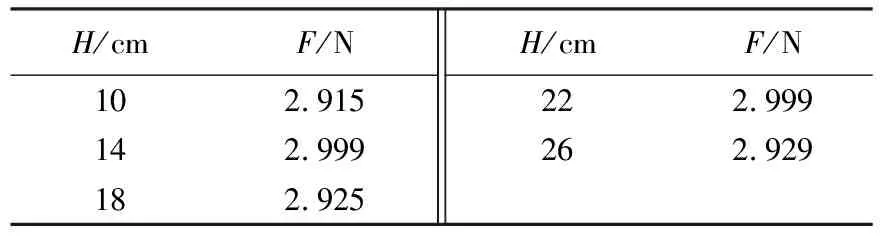
表4 最大波浪力随波高的变化(工况1)

定波高(18 cm)条件下，随着波浪周期增大，浮标模型运动减弱，A、C锚绳拉力呈梯度缓慢减小，最大差值约0.5 N，而B锚绳拉力显著减小，最大差值约2 N.A、C锚绳拉力变化规律相似，数值略有差异，最大差异为1.3 N.相比于工况1中B锚绳拉力几乎不变，工况2中B锚绳拉力呈现完全相反的规律.针对该现象，从冲量角度考虑，如表5所示，通过F=mΔv/t计算得到作用在浮标上的最大波浪力大幅持续减小，相应拉力传感器测得的锚绳拉力也在大幅减小.综合两个工况中B锚绳拉力变化，工况1中波浪周期不变，锚绳拉力变化不明显，工况2中波浪周期变大，锚绳拉力随之显著减小，均可以使用动量变化量加以解释，波浪周期对B锚绳拉力起主要作用，而并非波高.