三维激光点云降噪的优化方法

杨 倩 李沛鸿 吴玉泉

（江西理工大学建筑与测绘工程学院 江西赣州 341000）

1 引言

三维激光扫描技术（3D Laser Scanning）是一种能快速获取扫描物体表面模型的新兴技术，三维激光扫描仪可以快速扫描被摄物体表面多次，通过红外和近红外波长直接获取物体表面特征点的三维坐标信息，以捕获被摄物体空间几何采样点（点云）的几何结构和空间三维信息［1］。点云具有定义建筑物的3D几何形状的异质密度的作用。然而，常规的原始点云具有高密度和无组织等特点，会影响到后期模型建立的精准度而不能提供更好的定义。因此，需要对点云进行降噪。

对于散乱的点云数据，一般常用的方法是先进行格网模型的建立，然后对该格网模型进行降噪［2］。也可以直接对无序点云进行降噪。国外学者Desbrun［3］等提出的平均曲率流滤波方法能很好的解决顶点飘移问题。Fleshima［4］提出的基于双边滤波核的滤波法能有效的保留目标格网的特征性。拉普拉斯算法［5］简单易操作，还有法向量矢量滤波和顶点位置滤波相结合的综合滤波方法，均值飘移算法等［6-7］。对有序的点云常用的有最小二乘滤波，维纳滤波，卡尔曼滤波，中值、均值及高斯滤波等［8-9］。还有一些交互式去噪方法，如异常值过滤，深色扫描点过滤，离群点过滤，基于距离过滤点等。这些经典点的方法在运用到实际案例中时常常遇到一些特殊问题，有的会出现被测物体特征面产生弯曲和畸变，或是出现目标特征被过度光滑而导致模型模糊的现象。科学工作者们也针对相应的问题展开更深入的研究以达到完善的目的。

2 方法原理

2.1 点云邻域

对于我们获取的点云数据，在操作时除了要考虑点的几何属性和表面属性特征，还要考虑其周边点的各种信息，即每个数据点的邻域。在对点云数据降噪的过程中，除了要剔除噪声获取光滑的物体曲面，还要保留被扫描物体的特征点及面，防止模型过度光顺。邻域的选取至关重要，从某种程度上来讲，将直接影响到光顺去噪的效果。通常点邻域的构造方式有两种，即：欧氏距离［10］e构造出的局部邻域和k个最近点［11］构造出的局部邻域。本文在最小二乘滤波算法的基础上进行改进，优化后的算法通过对空间域和影响域的控制来限制邻域点的选取，从而获得与表面特征有关的自适应最优邻域。

2.2 最小二乘法降噪理论

基础的光顺去噪方法是最小二乘滤波，根据最小二乘法进行曲线拟合得到残差平方和最小的目标函数［12-13］，即:

最小二乘法假设x，y为不包含误差自变量，z为因变量，误差为 v，a0，a1，a2为曲面拟合系数［14］，其模型为：

基于最小二乘准则，可求出拟合曲面未知参数估计值

其中

点云数据集到拟合面的距离［15］：

再根据最小二乘拟合所设定的阈值与d值进行比较，大于设定阈值的点予以删除，达到降噪的目的。阈值的大小设定会直接影响到降噪效果，阈值过小，降噪效果不明显，阈值设定过大，又会造成有效点的缺失，所以很难选取合适的阈值。而且最小二乘法拟合是在假设x，y为不包含误差自变量，而z为包含误差的因变量情况下参与平面参数的解算，但实际上我们获取的点云在x，y，z三个方向上都有误差，所以最小二乘在点云数据平面拟合的解算处理中并不能取得良好的降噪效果。

2.3 改进的最小二乘法原理

本文采用一种改进的最小二乘法分别对每个研究面进行拟合，通过选取合适的邻域，建立合理数学模型及相关边界条件。该算法的主要思想：对每个研究面，将实测点云数据反代到建立的数学模型中，从而得到各个实测点到拟合的结构面的距离，记录该值为Da。搜索该点附近一定范围内所有实测点数b，若b不小于某正数m1，则说明该点非体外孤点，反之，将其删除。然后计算N个点分别到拟合平面的距离，并记录该值为Dab，统计在|Da-Dab|这个区间时，b个点落入该区间的个数n，若n小于某正整数m2，则该点为噪音点，将其删除。反之，将其保留。依次对该研究单元中的每个实测点进行上述过程的判别，直至遍历所有点。这种改进的算法通过对空间域和影响域赋予不同的权值，能够更精准的辨别噪音点，即使在有很多噪音点聚集在一起的情况下，也可以很有效的识别出来，达到降噪效果的最优。具体算法示意图如图1所示。

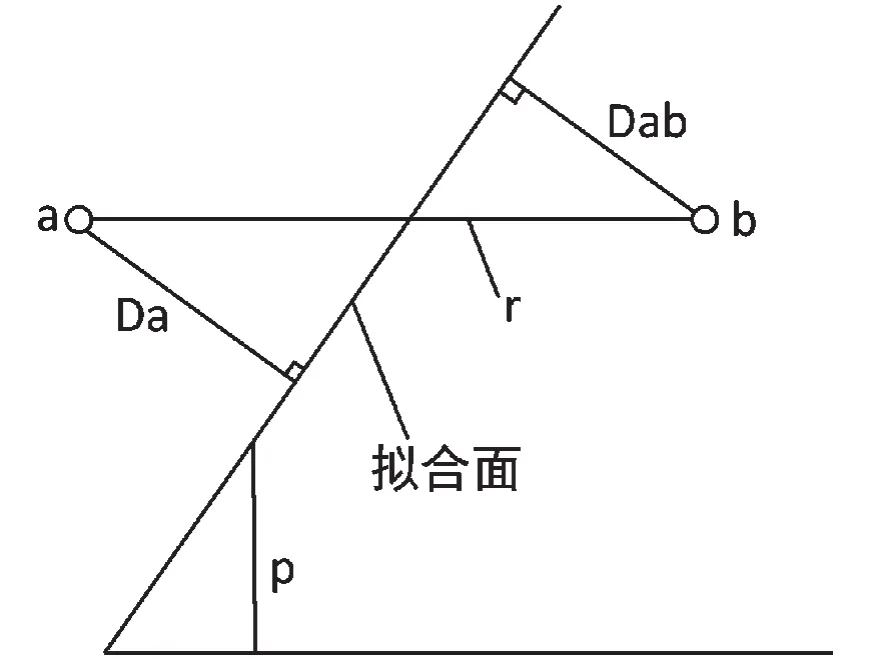
图1 算法示意图

3 实例实验

根据以上改进后的算法思想，得到如下图2的算法流程图，并以某一建筑标志扫描数据为例进行试验。为了确定数据处理过程中的边界条件及相关参数值，需要先设计模型试验进行定量分析。选择已经进行预处理的局部点云数据，利用上述点云降噪算法流程对试验点云数据进行降噪处理。

图2 点云降噪方法流程图

图3 原始数据

图4 模型对比效果图

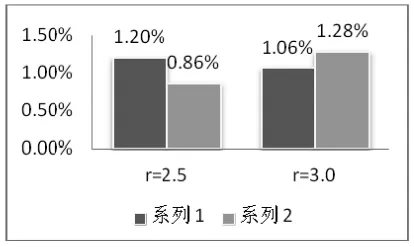
图5 点云删除率图

根据上述理论，设定4组试验方案参数进行原始数据（图3）的降噪，其中“2.5d-2-3”表示边界条件选择以半径为2.5的圆作为阀值，m1=2，m2=3，降噪后的点云数据效果如图试验1和试验2所示。当取3.0为阈值半径，又分别取m1，m2和为2，3进行试验。从上述试验结果可看出，取2.5为半径的阈值降噪效果均匀有序，效果明显优于半径为3的阈值，半径为3的阈值局部数据缺失明显，不宜选取。而在半径为2.5的试验中m1取3时，m2取3时保留了原始数据大概形态，获得较好的降噪结果。m1取2时，m2取3时点云被大范围删除，许多有效点云也被删除，取值不合理，也不予选取。再结合图5显示了两组的点云删除量，可以看到以2.5为半径的阈值中试验2中点云的删除率比较适中，以3为半径的阈值中点云的删除率过高，根据实际的空间目标物体得形态结构以及需满足的空间拓扑关系，本案例选取试验2（2.5d-3-3）的参数作为模型边界条件能取得做好的降噪效果。

相同的，我们利用最小二乘滤波对原始数据进行拟合去噪得到的降噪效果如图6所示：

图6 最小二乘滤波降噪图

由上图6可以看出，用基本的最小二乘滤波进行降噪，由于阈值选择不当，降噪后的点云很不均匀，而且建筑物的棱角特征被当作噪点被光顺，建筑物的特征不能够被很好的保留。对比之下，改进后的最小二乘降噪方法能较好的保留建筑物的属性特征，并且降噪后的点云均匀光顺，达到了较理想的效果。

4 结束语

由于三维激光扫描技术的优越性，在以后的生产生活中会有着更广泛的应用，选择更优化的降噪方法对于技术及生产质量的提高有着决定性的意义。传统的移动窗口最小二乘滤波只能适用于很小区域范围去噪，同时过分依赖所取窗口大小，改进后的算法可以帮助我们进行更优阈值及边界条件的选择，取得了较为理想的效果，为进一步优化降噪提供了借鉴。