基于改进ELM回归算法的地铁沉降预测方法研究

钟琛宜曾兴玉曹星星

（1.新余市国土勘测规划院 江西新余 338000；2.江西省测绘地理信息局机关后勤服务中心江西南昌 330209；3.南昌市测绘勘察研究院 江西南昌 330000）

1 引言

近年来，我国的地铁建设蓬勃发展，但地铁的安全问题也随之而来。一方面，地铁隧道的施工会不可避免地扰动地下岩体，使其失去平衡，从而造成地面沉降，另一方面地铁隧道的沉降也会一定程度上影响地铁运营的安全［1］。因此，有必要对地铁沉降进行长期连续的观测，鉴于此，很多科研人员通过分析地铁沉降的实测数据，并在此基础上进行预测，以获得地铁隧道沉降的未来趋势。由于地铁的不均匀沉降是一个非线性、非平稳的动态系统［2］，采用传统的回归分析法、时间序列分析法进行预测都会受到极大的约束，为此一些新的方法被引进来解决这一问题，如人工神经网络法（ANN，Artificial Neural Network）［3］。然而，传统的神经网络通常采用梯度下降法调整权值参数，存在学习速度慢、学习率难以确定及泛化能力低等缺陷［4］。针对这些问题，Huang等提出了极限学习机（ELM，Extreme Learning Machine）算法，该算法仅需一步计算即可确定网络的输出权值，大大提高了网络的学习速度和泛化能力［5］。本文结合经验风险最小化和结构风险最小化原理，进一步改进了传统的ELM回归算法，并在此基础上提出了一种基于改进ELM回归算法的地铁不均匀沉降预测模型。应用实例表明，该方法效果较好。

2 预测原理与方法

2.1 极限学习机（ELM）

极限学习机的网络训练模型采用最简单的单隐层结构，假设输入层、隐含层、输出层的节点数分别为m、N、1，则极限学习机的网络结构如图1所示。

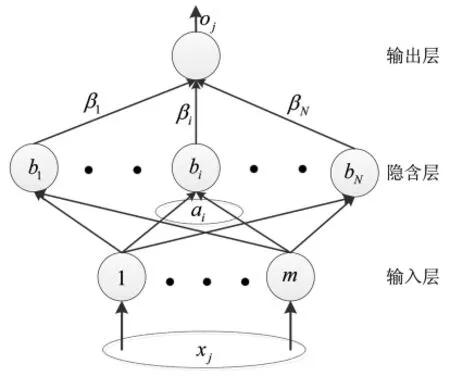
图1 极限学习机网络结构图

对于给定的数据集T={（x1，y1），L，（x1，y1）}，其中：x1єRm，yiєR，i=1，2，L，l。基于 ELM 的训练模型为

式中：βi、ai分别为输出层神经元和输入层神经元与第i个隐含层节点之间的连接权值；bi为第i个隐含层节点的偏置；h（x）=［G（ai，bi，xi），L，G（aN，bN，xN）］为隐含层输出矩阵；G为激励函数，一般选用sigmoid函数作为激励函数，表示为：

训练开始时，先随机选定初始输入权值ai和偏置bi，且在训练过程中ai值不再变化；输出权值βi则可通过求解下列线性方程组得到。

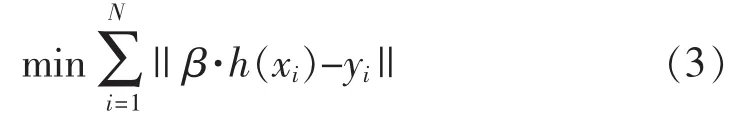
采用最小二乘法求解该线性方程组，并以输出矩阵H的Moore-Penrose广义逆H+表示，得到输出权值参数 β=H+·Y。

2.2 改进的ELM回归算法

ELM算法仍是采用以训练误差最小为衡量标准的经验风险最小化原理，这使得训练过程中会发生过拟合现象，降低模型的泛化能力［6］。针对这一问题，本文提出了一种结合经验风险最小化和结构风险最小化原理的改进ELM算法。

线性方程组（3）可转换为

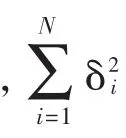
其中，αi为拉格朗日算子。由最优化原理，即令L对β、αi、δi的偏导皆为 0，则可得线性方程组

式中：y=（y1，y2，…yN）T，Iv（1，1，…，1）T，α=（α1，α2，…，αN）T， Ω 为方阵，Ω 的各元素值为

由式（5）、（6）可以看出，改进的 ELM 回归算法在建模过程中不再需要求解隐含层偏置值bi，提高了训练速率；且在改进的ELM回归算法中，综合考虑了经验风险和结构风险两大因素，可一定程度上降低发生过拟合的风险。

2.3 预测方法

基于改进ELM回归算法的时间序列预测方法流程如下：

1）归一化处理。在训练网络之前，需对数据进行归一化预处理，即将数据按比例线性映射至某区间，一般采用最大最小法。

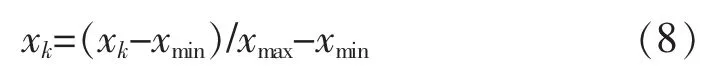
式中，xmin和xmax为数据序列中的最大、最小值；

2）确定延迟步数。为了确定最佳的网络输入结构，需确定延迟步数，对于时间序列（x），计算其延迟k步的自相关系数为r（k）

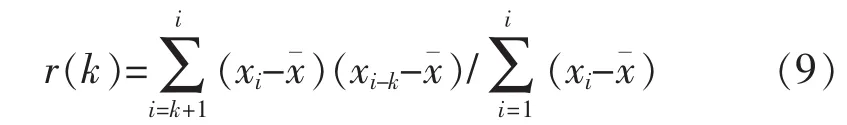
若 r（k）满足

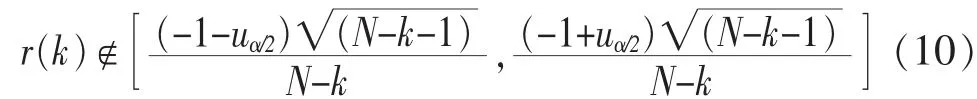
则称该时间序列延迟k步相关性显著，否则不显著［7］，取使 r（k）最大的 k 值作为最终的延迟步数m；

3）确定网络结构。上一步确定了延迟步数，由此可确定网络结构，输入层、输出层的节点数分别设置为m、1，隐含层节点数可设置为N=2m+1；

4）模型检验。训练模型，并通过测试数据检验模型精度，首先计算残差值ε（i）=xp（i）-xi（i），xp、xt分别代表预测值和测试值；再分别计算测试序列及残差的方差，得

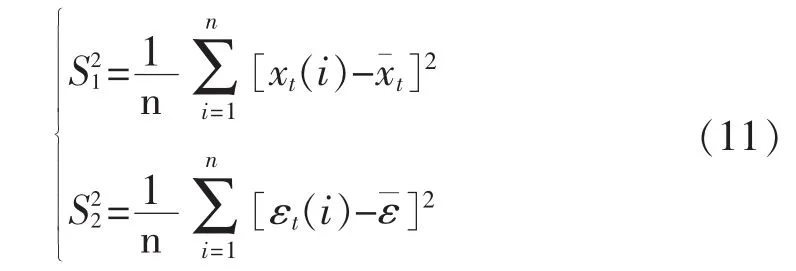
5）模型预测及结果分析。输入实测数据进行预测，采用均方根误差（RMSE）、平均相对误差和最大相对误差评定预测结果的精度。

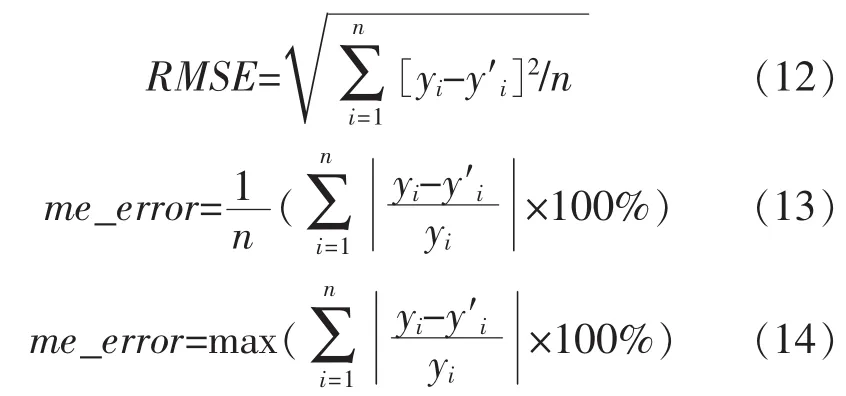
3 应用实例

为了验证本文提出的基于改进ELM算法的预测模型，采用某地铁隧道内一个沉降监测点最近7年的85期连续观测数据作为实验数据。选取前50期数据为训练样本，预测后35期的沉降值，并与实测数据进行对比。针对提前量为1期的沉降值进行建模预测，即采用前几期的沉降数据预测下一期的沉降，基本思想如图2所示。

图2 沉降预测的基本思想示意图

将原始数据归一化处理后，首先计算原始观测序列延迟 k（k取为 3～10）步的自相关系数为 r（k），得到最佳的延迟步数为5，从而确定了图1中的窗口宽度为5，即用前5期的数据预测第6期的沉降数据；通过反复训练（惩罚函数ζ设置为46.03）及模型检验最终确定了最佳的隐含层节点数为16，由此确定了用于预测的改进ELM模型网络结构为5×16×1。

为了验证本文提出的预测模型的优越性，另外采用BP和ELM进行训练和预测，激励函数均采用sigmoid函数，均多次训练以获得最佳的网络结构，三种模型的最佳网络结构分别为 5×25×1、5×14×1、5×16×1，预测的残差序列如图3所示。

由图3的预测残差曲线可以看到，本文提出的基于改进ELM回归算法的预测模型得到的预测残差基本分布-0.15～0.15mm之间，相比其余两种模型，本算法的预测结果与原始数据最为接近。

三种模型的预测结果比较如表1所示。

图3 沉降预测残差对比图

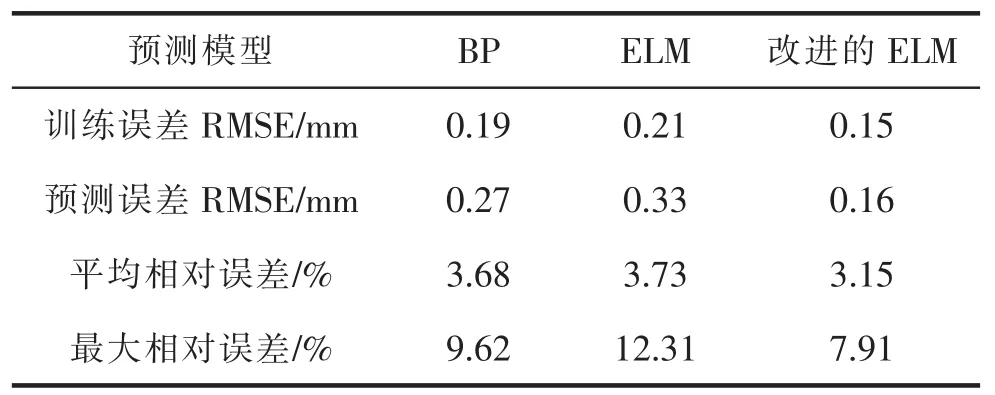
表1 三种预测模型的结果比较

由表1可以看到：

2）从预测误差（RMSE）来看，改进的 ELM 算法相对其余两种算法，其预测精度有了较大幅度的提升；

3）从预测结果的平均相对误差和最大相对误差来看，改进的ELM算法也显示出了其优越性。

4 结论

本文提出了一种结合经验风险最小化和结构风险最小化原理的改进ELM算法进行地铁的不均匀沉降预测。通过应用实例的检验，证实了改进的ELM算法在地铁沉降预测领域确实有很高的实用价值。