加权总体最小二乘法在点云数据平面拟合中的应用

吴璐璐陈汉清王乐洋

（1.江西水利职业学院建筑工程系 江西南昌 330013；2.河海大学地球科学与工程学院 江苏南京 211100；3.东华理工大学测绘工程学院 江西南昌 330013）

1 引言

总体最小二乘算法（TLS）在近30年来得到了充分的发展与广泛的应用，它能同时顾及观测值误差并同时考虑模型系数矩阵误差，是一种能够有效处理变量含误差模型（EIV模型）的数学方法［1］。当数据之间不独立或是系数矩阵中数据不等精度时，需要考虑系数矩阵元素之间以及观测值之间的定权问题，则要使用加权总体最小二乘法（WTLS）。测绘学科中加权总体最小二乘算法的发展主要在近些年，2013年Malengo A［2］提出基于拟牛顿法的加权总体最小二乘方法。本文以点云数据平面拟合模型为基础，将最小二乘算法（LS）、TLS以及基于拟牛顿法的WTLS应用到点云数据平面拟合模型中。通过仿真模拟数据和实际点云数据对这三种算法进行了比较与分析，得出了一些有意义的结论。

2 拟牛顿法

当EIV模型的函数为：

式中y为n×1的观测向量，A为m×n的系数矩阵，ey为观测向量的随机误差，EA为系数矩阵的随机误差，x为m×的待求未知参数。式（1）中由于存在EAx这一项，因此EIV模型是一个非线性模型。误差向量ey和vec（EA）的均值向量和协方差矩阵为

式中，Qy、QA分别为误差向量ey和eA的协因数阵，表示单位权方差，vec（·）表示矩阵的拉直变换。

用求解约束优化问题［3］的方式来处理式（1）的总体最小二乘方法得：

其中，eA=vec（A-），表示系数矩阵的真值，（A-EA）x=（xT⊗In）vec（A-EA）。

考虑到EIV模型的本质为一特殊的非线性模型，因此可以采用非线性最小二乘估计理论进行参数求解，本文在Malengo A［2］文献的基础上推导了基于拟牛顿法的WTLS。

利用非线性优化理论方法［5］求解未知参数：

其中，x（k+1）、x（k）为未知参数的全量形式，dk表示该算法中的搜索方向，αk为dk的系数。式（5）的求解关键在于搜索方向dk的确定，在拟牛顿法中，dk与目标函数的二阶偏导的近似矩阵和梯度函数有关，可以通过下式进行确定：

其中，Hk用于近似表示目标函数Φ的二阶偏导矩阵的逆矩阵。

基于拟牛顿法的WTLS的迭代步骤阐明如下：

第一步：给定观测数据A、y，根据函数模型结构确定 Qy、QA，设置 k=0；

第三步：计算系数αk

第四步：计算

3 点云数据空间平面拟合模型及加权总体最小二乘算法

3.1 点云数据空间平面拟合模型

假设点云数据平面方程式为［6］：

式中，a、b、c为点云数据平面拟合参数。把式（7）写成矩阵形式为

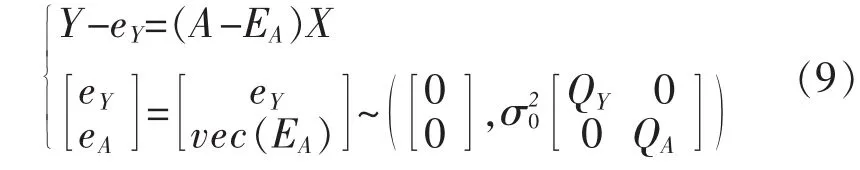
式中，eY为观测向量Y的随机误差矩阵，EA为系数矩阵 A 的随机误差矩阵；，表示EA列向量化后得到的矩阵；σ20为验前单位权中误差；QY，QA分别表示观测向量协因数阵和系数矩阵列向量化后的协因数阵［7］。

根据eA值和相关权值的设置，采用不同的方法解算点云平面拟合参数估计：

方法一：eA=0，此时仅有观测向量的误差，EIV模型变为测量平差G-M模型：

使用最小二乘解法解算参数估值。

方法二：eA≠0，QY=In，QA=Inm，此时假定点云数据是独立等精度的，QY，QA均为单位阵，使用总体最小二乘法解算参数估值。

方法三： eA≠0，QY≠In，QA≠Inm，此时假定是不等精度的点云数据。运用WTLS求解参数估值［7］。

3.2 空间平面拟合模型的加权总体最小二乘算法

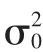
式中，θi为 i点入射角余弦值，（a，b，-1） 为平面法向量，（xi，yi，zi）为点 i的三维坐标。

设点云数据在x、y、z方向上是等精度观测的，则有σx=σy=σz。根据系数矩阵A的特点，设计相关的权阵：

式中，P0为 A 的列向量之间的权阵；PX=PY∈Rn×n，它们与入射角余弦值cosθi有关。

对应的协因数阵为［9］：

由Q0和QX可算系数矩阵协因数阵［9］：

4 算例分析

本文的原始点云数据通过三维激光扫描仪对地面扫描获得，如图1所示。分别利用基于拟牛顿法的加权总体最小二乘、总体最小二乘和最小二乘对样本点云数据进行拟合，获取平面拟合参数以及单位权中误差。由式（15）计算点到拟合平面的距离 di，平面拟合精度。

式中，n为观测点个数。

不同算法优劣的评判指标使用单位权中误差和平面拟合精度。利用三种算法对仿真模拟数据和实际点云数据进行点云数据平面拟合。

4.1 仿真模拟点云数据平面拟合

根据点云数据平面拟合方程式z=ax+by+c，随机确定一个平面［7］，例如 z=x+3y+1，即参数真值 a=c=1，b=3；在该平面随即抽取100个点，如图1所示，各点（xi，yi，zi）加入均值 u=0，方差=σ2/cosθi的随机误差；模拟10次，取每个参数均值作为每个参数的最终结果，具体各参数计算结果及精度评定指标见表1。

图1 模拟点云数据

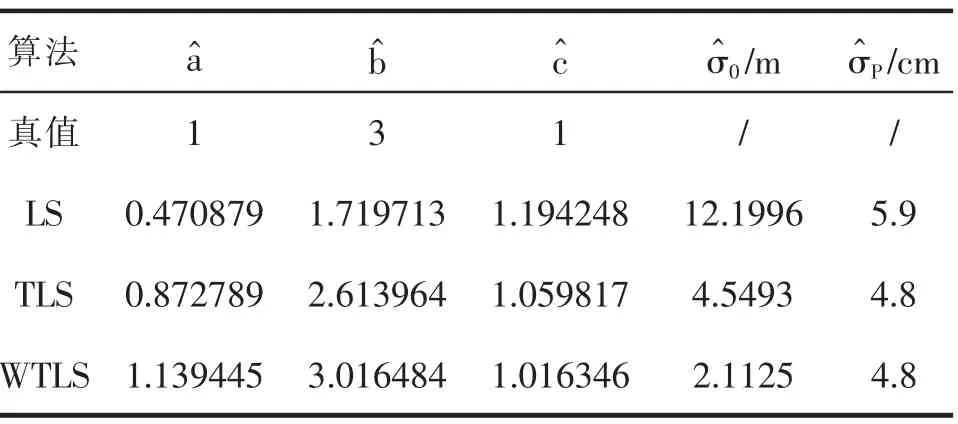
表1 各方法点云数据平面拟合计算结果

从表1能够看出，基于拟牛顿法的WTLS法求解的参数估值距离真值最近，TLS次之，LS求解的各参数与真值相差最远；在单位权中误差上，WTLS比LS和 TLS分别提高了 83%和 54%；WTLS、TLS、LS的平面拟合精度分别为4.8cm、4.8cm和5.9cm；综合两个精度评判指标，WTLS方法平面拟合效果最优，TLS次之，LS拟合效果较差。

4.2 实际点云数据平面拟合

使用三维激光扫描仪对地扫描，获得一组原始点云数据，经过剔除粗差后，获取一组点云数据。如图2

图2 地面点云数据

表2 实际点云数据平面拟合计算结果

从表2可以看出，在单位权中误差上，WTLS比LS和TLS分别提高了76%和63%；WTLS、TLS和LS的平面拟合精度皆为1.09mm，造成这样的原因是因为三种方法求解出的参数估值较为接近；综合两个精度评判指标，WTLS拟合效果最优，TLS次之，LS拟合效果较差。WTLS引入相关协因数阵，得到更优的平面拟合模型和更高精度的参数估值。

5 结论

通过模拟算例和实际地面点云数据平面拟合算例验证了WTLS在点云数据平面拟合中获得比TLS和LS法更精确的参数估值；根据点云数据精度与入射角的关系，确定相关协因数阵 Q0，QX，QA，得到的中误差和平面拟合精度比TLS和LS更小，得到的参数解更优；由于系数矩阵A存在随机误差且第三列为常数，引入的列向量Q0，能得到更合理的解算模型。本文中的加权总体最小二乘法继承了拟牛顿法求解非线性优化问题的优点，不需要目标函数二阶导数的信息，此算法有它一定的优势，可以考虑在其他的模型中加以运用。