使用规则挖掘实现排程系统的规则制定

2018-07-21

制造业自动化 2018年7期

（北京机械工业自动化研究所有限公司，北京 100120）

0 引言

在中国制造2025的大环境下，越来越多的企业选择将具体的生产业务与ERP、MES等信息化系统相结合，利用信息化的手段来管控，指导制造生产。而在这其中，对于实际的生产计划的计划调度则是十分重要的。高级计划与排程系统（APS）通过对计划、资源、时间等进行管理从而达到最大化效益的目的，可以十分有效地管理企业的生产计划。尽管APS系统的理论已经非常丰富，在实际生产中的运用效果却不是很理想。这一情况的出现有多种原因，其中一个原因就是实际生产中的生产规则太过于复杂和多变，企业的生产人员也无法很清晰地将实际生产规则总结提炼为通用的规则，导致排程系统排程的结果并不是很准确，需要频繁的人工干预，从而使得效率大幅度降低。

然而，绝大部分的企业在生产过程中都会保留生产信息，这些大量的生产信息中暗中包含了企业生产的相关规则，所以可以利用规则挖掘方法以及粗集理论来对通用生产规则进行总结与归纳，也可以利用不断产生的生产信息进行自学习，得到更加具有普适性的生产规则，从而更高效地指导生产，并且可以根据实际生产情况的变化而对排程规则进行更新，可以更准确地指导生产。

1 粗集理论的基本概念

知识是对对象进行分类的规则，对象是用属性集表示的，而知识则是属性集之间的映射关系。对属性集进行映射就会产生不同的分类，而这些分类就是知识。

根据粗集理论，一个规则体系可以表达为S=（U，C∪D，V，f）。其中U={X1，X2，…，Xn}代表对象集合，A=C∪D代表属性集合，子集C代表条件属性集，子集D代表决策属性集。并且有C∪D=A，C∩D=φ。若规则体系用二维表的方式表达，那么可以称这个二维表为决策表，在这个表中每一行表示一个元素，每一列表示其属性。

设U为对象的有限集，称之为论域，对于任何子集X∈U，都可以称X是一个U中的概念，U中的任何概念组可以称之为关于U的抽象知识，简称知识。若有集合R={X1，X2，…，Xn}，其中Xi∈U，Xi≠φ，并且Xi∩Xj=φ，当i≠j；i，j=1，2，…，n；且有∪ni=1Xi=U，则称R为一个分类，Xi称为R的一个等价类。论域U中的一个分类确定了U上的一个等价关系。同样，论域U中的一个等价关系也确定了论域U的一个分类，所以可以利用等价关系对集合进行分类。

属性集A中的属性分为条件属性C与结论属性D；确定条件属性集上的等价类E_k与结论属性集上的系统概念X，寻找Ek与X件的关系，若其结果有X包含Ek，则成为下近似；X与Ek的交集非空，则称为上近似；X与Ek的交集为空，则称为两者无关；根据上述结果确定发现的规则，下近似中的条件属性与结论属性之间可以建立确定性规则，上近似中的条件属性与结论属性之间可以建立不确定性规则，而无关说明条件属性和结论属性毫无规则可言。基于粗集理论的知识发现主要涉及两个重要的处理过程：求近似控件和缩减。实现规则发现的一个具体方法是通过在近似空间中寻找条件属性关于结论属性集中的最小依赖关系来完成的。

粗集理论的特点是不需要预先定某些属性或者特征的定量描述，而是直接从给定问题的直接描述出发，通过不可分辨关系确定问题的近似域，从而找出该问题所对应的知识，即为对象进行分类的方法。

2 利用粗集理论与决策挖掘的APS排程规则提取

利用粗集理论和决策挖掘方法提取APS排程规则的主要过程如图1所示。

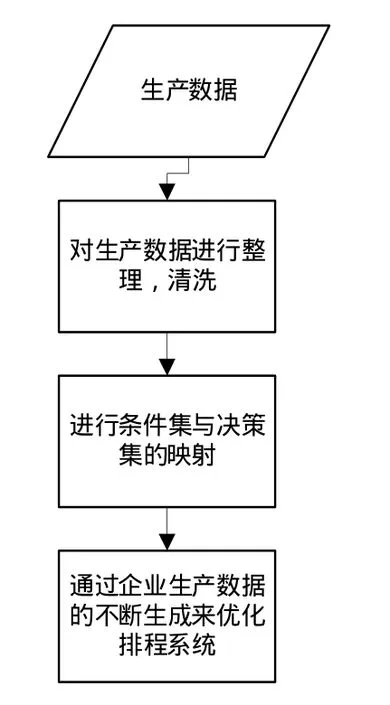
图1 规则提取过程

如图1所示，首先得到企业的实际生产数据，此时需对企业的生产数据进行整理与清洗，得到标准格式的条件属性集-决策属性集生产数据。然后利用粗集理论与规则挖掘的方式对生产数据进行条件集与决策集的最小映射，挖掘出的映射关系即为规则，最后在企业的不断生产中，生成新的生产数据，系统根据新的生产数据不断的进行优化学习，使得排程规则更全，排程更加准确。

基于以上提到的粗集理论，我们在得到了企业的生产数据进行整理得到，时间-产品-设备的具体信息，其中时间可以作为权重系数，时间太久的规则可以降低权重甚至作废。

首先我们对生产的设备进行分类，由于生产的设备一般不会有很多种类，所以这一步由人工进行分配，比较极端的情况有两种：第一种是所有设备全部都一样，不需要进行分类。这个时候也不需要进行排程规则的提取，因为没有任何限制，这时候只要根据企业具体生产实际情况，将产品的生产计划分配到具体的设备上进行生产就可以。第二种情况是全部的生产设备全都不一样，即每个设备为一个分类，这时候就不需要人工对设备进行分类了。此时只要根据历史数据对产品和生产设备之间的规则进行抽取即可。

我们取最普通的情况，即有n种产品，有m个生产设备。其中m个生产设备可以划分为M组，我们认为每组生产设备可以生产的产品种类完全相同。即找到属于生产设备的最小集合。假设M可以表示为M={M1，M2，…，Mn}，则根据生产的历史数据中产品曾经在某个生产设备上面生产过的信息可以得到ni∈Mj,i,j∈R。这样我们其实就得到一条规则，即产品ni可以在设备集Mj上进行生产。然后按照历史数据不断的将产品信息与设备集信息进行对应，这样我们就可以得到一个产品与设备集对应的关系。

这样，只要企业的历史生产数据足够大，那么理论上历史数据是可以包含所有生产情况的，根据一个粗略的判断法则，当一个分类拥有5k个已经标注的样本时就可以达到可以接受的性能，当拥有一千万已经标注的样本时就可以达到甚至超过人类进行判断的准确性。依据这个法则，我们可以大致的估算一下我们得到的粗集规则是不是可以使用。当然，如果不是非常准确也没有关系，因为在APS系统根据这个规则集进行排程之后，计划人员可以手工对排程结果进行干预，比如在原规则集中没有产品n1可以在设备集M1上生产的记录，那么排程系统就不会将产品n1排程在设备集M1上进行生产，但是如果计划员在进行确认排程结果的时候认为产品n1可以在此设备集上进行生产，那么通过人工对排程结果进行干预，将产品n1排程在属于此设备集的任意设备上面进行生产，那么系统就可以自动记录这么一条规则，从而在下次对这个产品进行排程的时候也会将设备集M1作为备选生产设备考虑进去，这样就会令计划排程的结果越来越准确。

3 具体实现以及规则评价

3.1 具体实现

我们以某橡胶密封圈加工企业作为测试对象，该企业每周生产六天，每天分为三班，每班生产的产品有可能和下一班次一样，也有可能不一样，并且班中也有可能换产品生产。如表一所示，我们收集了该企业82台设备近一年的实际生产情况，一共102641条记录，如表一所示，即每个班次每个设备上利用什么模具生产什么产品的相关信息。

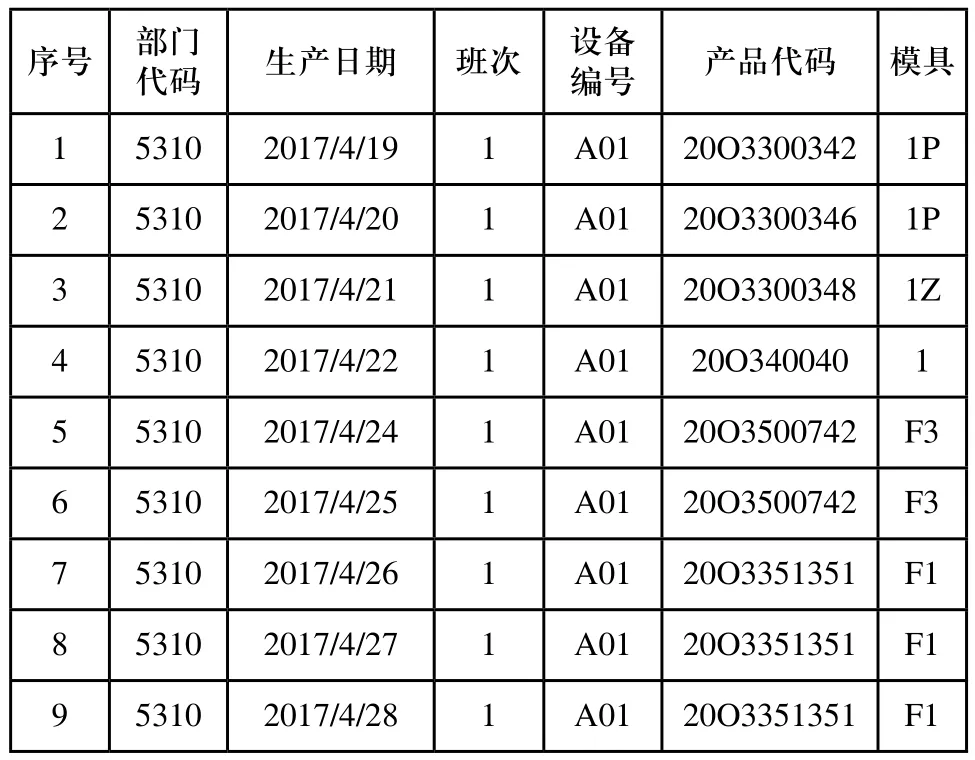
表1 部分企业实际生产数据表

按照产品-模具作为条件，即产品代码和模具代码都相同的记录会被视为相同的条件，按照这种分组方法可以将分为2030组。

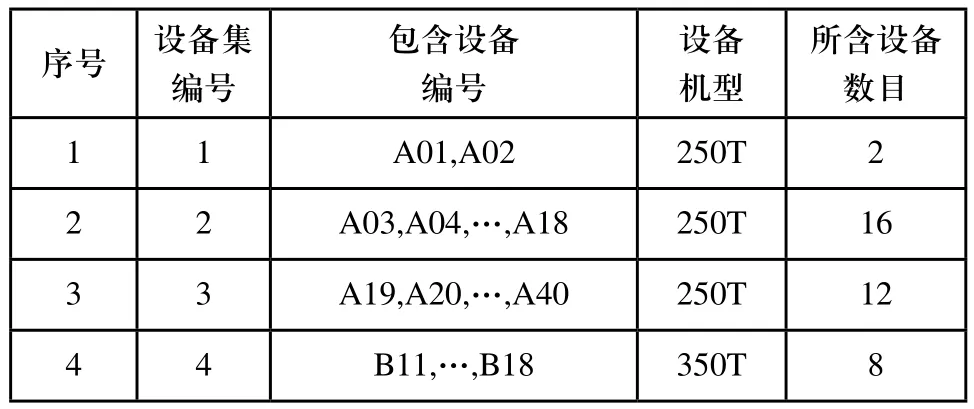
表2 部分设备集合表

然后如表二所示，手工将8台设备分为9个集合，保证每个集合中的机器都可以生产相同的产品。

图2 规则表达方式

如图2所示，由人工对生产排程的规则进行梳理，产品-模具作为条件集，设备作为属性集，将条件集与属性集对应即为一条规则。按照产品-模具-设备分组可以分出6658条规则，作为系统自动对产品-模具-设备集合进行规则抽取的对照组。然后再利用上文描述的方法，在系统中自动将产品-模具-设备集信息进行对应，进行相应的规则抽取。从而得到一个粗集规则表，这个表就代表了对应的产品，对应的模具应该在哪些设备集上面进行生产，我们一共抽取出了5171条规则。将两个规则集中的规则进行一一对比后，相同的规则集有4263条。

3.2 规则评价

由此，按照得到的规则来算，系统自动得到了4263条规则，实际准确的规则有6658条，自动抽取规则的准确率达到了0.64。当然由于每个设备集合中所含的设备数目是不同的，所以在规则抽取中寻找出设备数目较多的集合明显比设备数目较少的集合要更有价值。此时我们再将设备集合中的设备数作为一个权重加入计算准确率的公式，即对于每个产品-模具条件，自动抽取规则的准确性X=numtest/numco，numtest表示系统自动抽取规则所得到的设备数目，numco表示准确的规则中所包含的设备数目。对每一个产品-模具条件计算准确性之后，再做一个平均，可以得到此时的准确性已经达到0.789。此方法的最大特点是可以快速进行部署，只需要对得到的生产数据进行简单的数据清洗，就可以快速地得到较为准确的结果，并且可以在以后的生产中自动地不断优化。