出药机构动力学仿真及优化分析

（北京信息科技大学 机电工程学院，北京 100192）

0 引言

当前在我国医院药房取药过程中，患者常常排队等药，发错药的事故也时有发生。传统的医院储药系统主要由普通的药架构成，药品的存储密度低，药品的发送基本上是由医务人员根据处方人工配送，这种模式的发药速度慢，效率低。实现药房自动化不仅可以帮助医院提高发药的速度更能增加发药的准确度。采用机械手式的自动存取设备出药不仅速度慢、控制电路繁琐、且可靠性差。为解决上述问题，本研究提供了一种出药快捷，工作可靠的出药机构[1～4]。

1 出药机构原理

出药系统主要包括平行排列的斜坡储药槽和出药机构。出药机构主要由电磁铁线圈、电磁铁铁芯、出药机构底座、连杆、摇杆、挡药滚轮、导向滚轮；挡药滚轮设置在斜坡储药槽前方，送药时对药盒起导向作用，导向滚轮铰接于摇杆前端。如图1所示。

出药单元与水平方向成25°角放置，在电磁铁线圈不通电的状态下，摇杆与出药机构底座的方向平行，挡药滚轮挡住药盒，将其挡在储药槽上；在电磁铁线圈通电的状态下，电磁铁的铁芯与线圈吸合，拉动连杆继而拉动摇杆向上倾斜，把药盒顶高，当药盒前端底部高于挡药滚轮时，药盒借助重力经由导向滚轮导向滑出。当电磁铁的拉回动作结束后，电磁铁铁芯在弹簧的复位作用下回到初始位置。

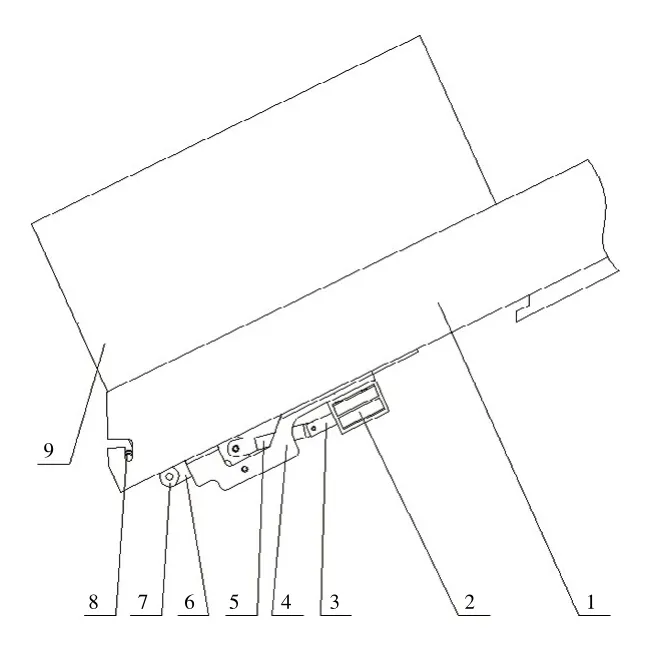
图1 出药机构结构示意图

这种出药机构结构简单，快速准确，且可靠性高。实现了大型药房药品的自动发放，节约了人力成本，提高了工作效率。

2 出药机构受力分析

如图2所示，将出药机构简化为一摇杆—滑块机构，进行受力分析。药盒在弹射过程中，电磁铁提供拉力FM，摇杆前端受药盒阻力F。

采用复数矢量法对该机构进行受力分析，以A点为原点建立直角坐标系，并将各构件的杆矢量及方位角示出。将各运动副中的反力统一表示为FRij的形式，即构件i作用于构件j上的反力，且规定i＞j，二构件j作用于构件i上的反力FRji则用-FRij表示。再将各运动副中的反力分解为沿两坐标轴的两个分力示出。

图2 杆件受力分析简图

选取运动副B为首解副，并取构件1为分离体，并将诸力对A点取矩，则根据得：

由上式的实部等于零可得：

由上式的实部和虚部分别等于零可得：

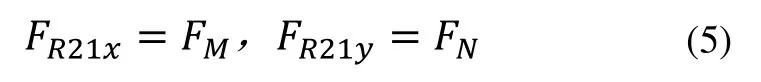
将上式带入式(1)，得：

又由FN=FM.tan(180°-θ2)=-FMtanθ2，上式可化为：

3 药盒动力学分析及仿真

3.1 药盒动力学分析

出药机构上药时，药盒重力在平行于药槽方向的分力应大于药盒和药槽之间的静摩擦力，即：

式中fs为药盒与药槽间的摩擦系数，此处取值为0.13。

出药机构进行出药动作时，药盒在摇杆的作用力下脱离药槽做平面运动，包括质心的抛物运动和绕质心的转动。根据力的平移定理和合力矩定理，将药盒所受的力系简化，并将药盒作为刚体处理。简化后的药盒受力情况如图3所示。

图3 药盒受力分析模

在药盒被摇杆顶起时，药盒在竖直方向受重力G，平行于药槽方向受到挡药滚轮的支持力FN，以及在与摇杆接触点处受到摇杆的作用力F。在如图3所示瞬间，刚体平面运动微分方程在自然直角坐标轴上的投影式为：

解得药盒被顶起瞬间质心加速度与角加速度：

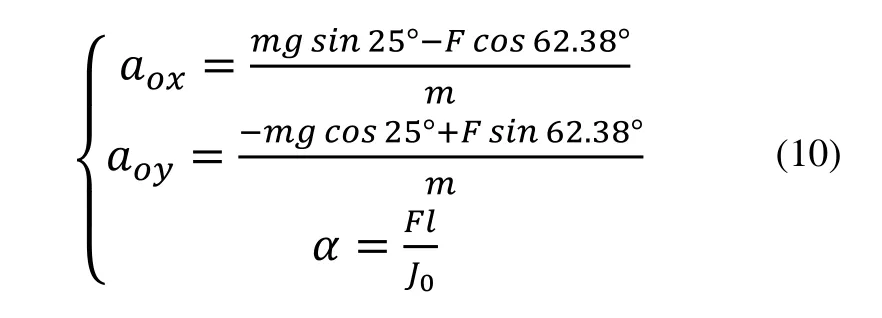
式中l为力F对O点的力臂，l=55.46mm；J0为药盒对重心O的转动惯量，其中a、b分别为药盒的长度和宽度。

3.2 基于ADAMS的药盒动力学仿真分析

3.2.1 虚拟样机模型的建立

由于虚拟样机技术在进行运动学、动力学求解时，只考虑零件的质心和质量，而对零件的外部形状不予考虑。因此，要对出药机构的形态结构进行适当的简化[5]：

1）各铰接处以转动副来约束，等效实现二者的相对运动；

2）各部件为刚体；

3）忽略转动副摩擦。

根据出药机构实际形态结构，按照以上原则，建立了虚拟样机模型，如图4所示。

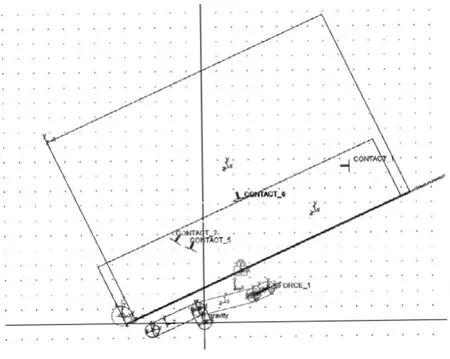
图4 出药机构虚拟样机模型

根据电磁铁吸力特性，分别对通电率为50%与25%时两种情况进行仿真，电磁铁吸力特性曲线如图5所示。

图5 电磁铁吸力特性曲线

3.2.2 仿真分析

仿真结果如图6所示，其中图6(a)和图6(b)分别为通电率为50%和25%时出药机构仿真结果。

如图6(a)、图6(b)所示，左上图为药盒弹射过程，其中黑色曲线为药盒质心的运动轨迹。右上图为药盒的角加速度曲线，左下图为药盒质心在水平方向的速度曲线，右下图为药盒质心在竖直方向的速度曲线。可见药盒在弹出后的运动包含抛物运动及绕其质心的旋转运动，因此需根据药盒的运动轨迹合理选取弹出点与输送装置的高度差和水平距离等参数，防止药盒掉落时脱离输送装置或发生倾覆。

4 出药机构优化分析

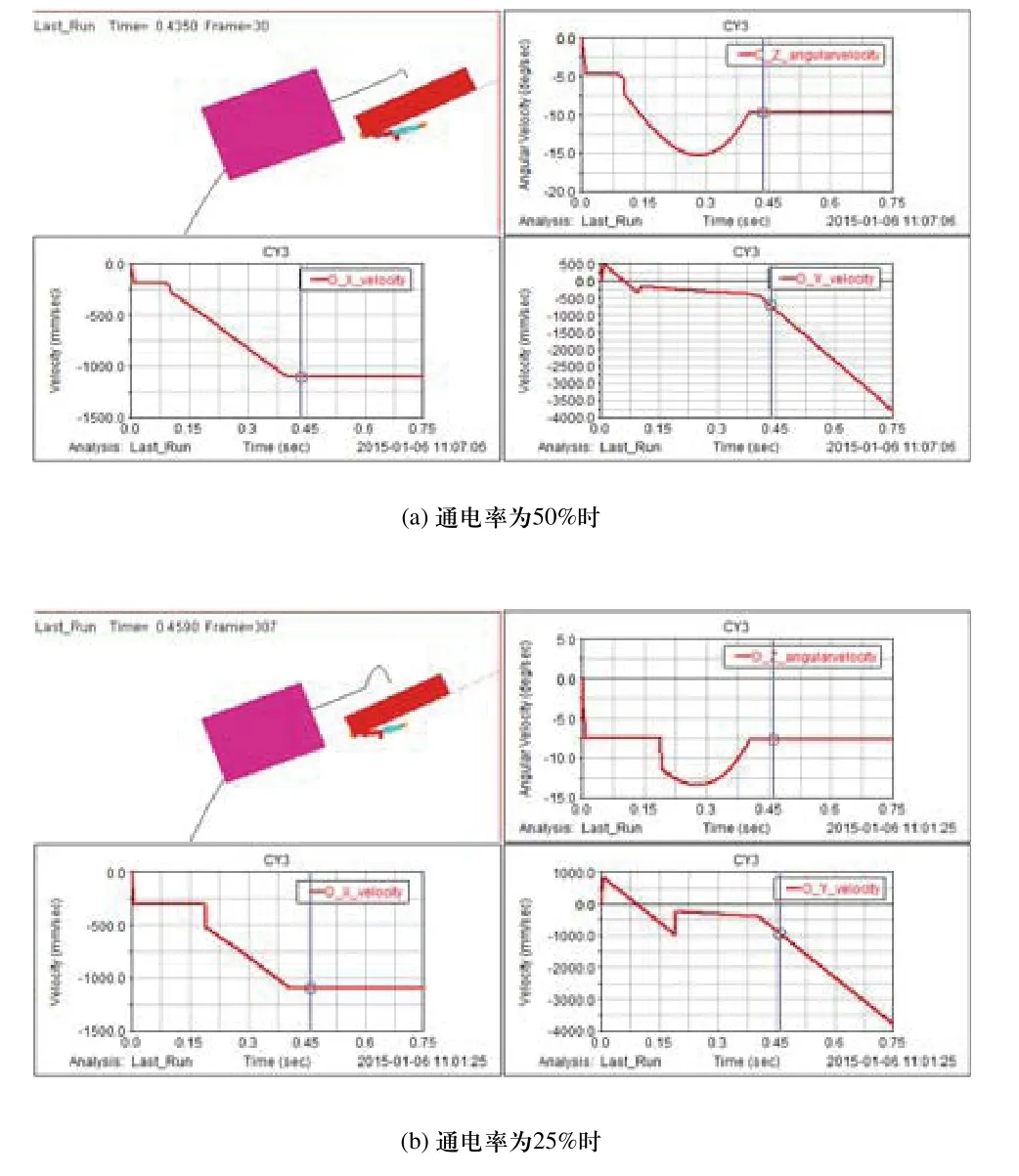
图6 出药机构仿真结果

由于储存在药槽中的药盒质量不同，被弹射出来的运动轨迹也不一样，质量小的弹射距离高，质量大的弹射距离低。且当出药机构的输出力不合理时会使药盒无法被弹起或超出合理弹起高度。因此需基于药盒初速度最大化对出药机构各杆件参数进行优化设计，使不同种类的药品在空中的运动轨迹最优化[6]。

由于摇杆-滑块机构由LAB、LBC、LBD等参数确定，式(6)表明摇杆作用力与LAB、LBC有关，因此取设计变量为：

以药盒质心垂直于药槽的初速度最大为寻优目标函数，以确定最优杆长方案，取目标函数为：

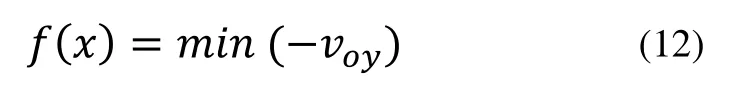
约束条件的建立首先应满足构成偏心摇杆-滑块机构的杆长条件，即LAB+e≥L_BD，其中e为偏距，其值为3.5。同时受于空间位置约束，LAB与LBC不能太长。

确定设计变量、目标函数和约束条件后，采用ADAMS对虚拟样机进行参数化建模，采用设计研究模块使各设计变量在一定范围内进行取值，根据设计变量值的不同进行一系列仿真分析并输出各次仿真分析的结果，找出哪些设计变量对目标函数的灵敏度最高。

灵敏度表征目标函数对设计变量值的变化的敏感程度。灵敏度分析是优化设计的铺垫工作，用来确定重要的设计参数，通过预订参数定量分析每个设计参数对目标函数影响的程度，从而缩小研究范围，在优化设计时做重点考虑[7,8]。灵敏度大小以前后两次试验灵敏度的平均值表示[9]：

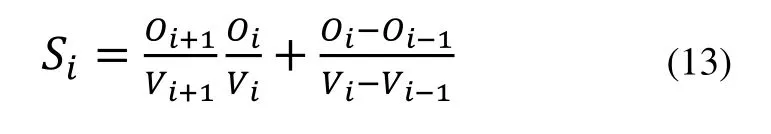
上式中：O为目标值，V为设计参数值，i为迭代次数。

LAB、LBC、LBD各自变化对目标函数的影响曲线分别如图7～图9所示。

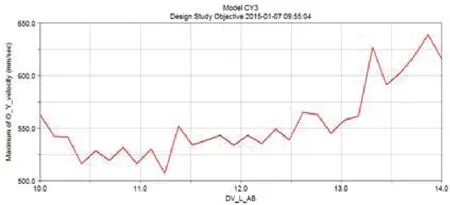
图7 LAB变化对目标函数的影响曲线

图8 LBC变化对目标函数的影响曲线

图9 LBD变化对目标函数的影响曲线

其中LAB取值为13.172时灵敏度值最大，为249.01；LBC取值为40.724时灵敏度值最大，为136.12；LBD取值为47.517时灵敏度值最大，为271.74。

通过试验设计模块对多个设计变量的取值组成组，研究在设计变量取不同的可能组合时目标函数的取值情况，进行优化求解。求解过程中各次迭代的曲线变化如图10所示，其中横坐标为迭代步，纵坐标为药盒质心垂直于药槽的初速度值。

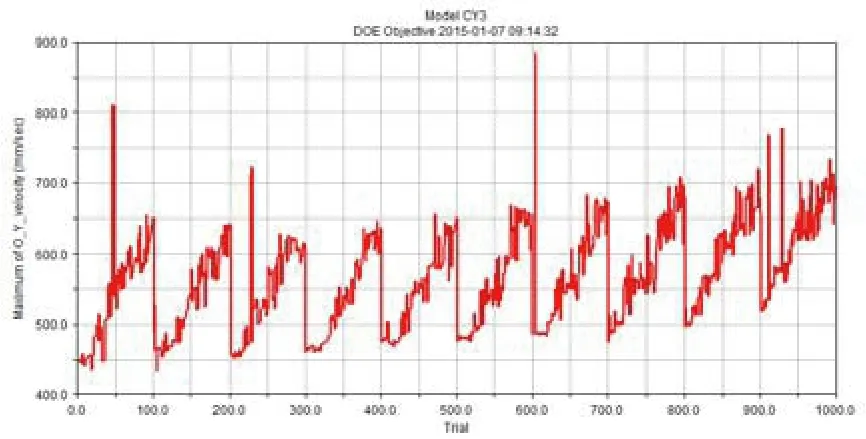
图10 优化迭代曲线

最优解为第604迭代步，其设计变量取值为：

由优化结果可看出，优化后药盒质心垂直于药槽的初速度voy=885.13。

5 结论

阐述了出药机构的原理及动作过程，对出药机构和药盒进行了受力分析。建立了出药机构的虚拟样机模型，并对其进行了基于ADAMS的动力学分析，得出了在不同电磁铁通电率下的药盒质心轨迹曲线。对出药机构进行了优化设计，并对各设计变量进行了灵敏度分析，得到了药盒质心垂直于药槽的初速度最大时出药机构的各杆长最优解。综上，本研究为机构设计提供了实用方法，为出药机构最终的尺寸设计提供了依据，为药房自动化系统设计奠定了理论基础。