一种新型3-RPS并联机构的刚度特性分析
2018-07-21
(山东理工大学 机械工程学院,淄博 255049)
0 引言
并联机构由于并联支链的存在,使其具有承载能力强、定位精度高等一系列优点[1~3]。随着研究人员对并联机构研究的深入,人们发现机构静刚度对机构的定位精度等方面具有重要影响[4]。目前,针对并联机构静刚度的分析方法有有限元法[5]、解析模型法[6~8]。栾玉亮等[5]基于有限元法对3-PPSR柔性并联机器人的静刚度进行了分析。对于解析模型法,最早是由Gosselin[6]基于机构速度雅克比矩阵提出的静刚度解析模型。在此基础上,Wang等[7]对一种滑块式并联加载机构的静刚度进行了分析。赵福群等[8]提出了一种支链含有闭环单元的3-5RS并联机构,基于速度雅可比矩阵建立了该机构的静刚度模型。
有限元法虽然方便快捷,但是无法建立机构静刚度与机构尺寸参数、位姿参数之间的数学关系。对于以3自由度为代表的少自由度并联机构,其速度雅可比矩阵并非6阶方阵[9~11]。因此,基于速度雅可比矩阵所建立的静刚度解析模型不能定量描述动平台非自由度方向上的位姿变形量。胡波等[12]基于虚设机构法建立了传统3-RPS并联机构的完整静刚度模型,但对于其他同类型的少自由度并联机构,文献对如何虚设运动副并未给与详细说明,该方法在实际应用过程中也会受到一定限制。
对于转动副轴线平行布置的新型3-RPS并联机构,本文从支链单元柔度矩阵角度出发,所建立的机构静刚度模型能够完整描述动平台在机构自由度方向以及非自由度方向上的位姿变形量,更加符合动平台位姿变形的实际情况,尤其适用于少自由度并联机构的静刚度分析。
1 3-RPS并联机构结构描述
3-RPS并联机构由动平台、定平台以及连接动平台和定平台的三条支链组成,如图1所示。

图1 3-RPS并联机构简图
每条支链由下往上分别为转动副R、移动副P和球铰副S,动力输入为各支链移动副。转动副按顶角为120°的等腰三角形布置(腰为R1R2和R1R3),球铰副转动中心按等边三角形布置,并且等边三角形S1S2S3的高与等腰三角形R1R2R3底边高相等。以定平台底边R2R3的中点O1为原点建立定坐标系O1x1y1z1,以动平台几何中心点O2为原点建立动坐标系O2x2y2z2。转动副轴线平行布置且与定坐标系轴O1y1平行。因此,由机构的结构关系可知,动平台的自由度为沿坐标系轴O1x1、O1z1的平移和绕坐标系轴O2y2的转动。动平台的位姿可表示为[x,z,θ]T,其中x和z为动平台参考点O2在定坐标系中的坐标分量,θ为动平台外法线与定坐标系轴O1x1的夹角。
2 单条支链末端变形量
在建立机构静刚度模型过程中,将定平台和动平台视为刚体,仅考虑三条支链弹性变形,且忽略各运动副的间隙和摩擦对机构静刚度模型的影响。因为球铰副S对构件j的末端存在约束力,支链发生弹性变形,如图2所示。构件i和构件j的变形属于弹性极限范围之内的小变形,因此符合小变形叠加原理。在坐标系Ojxjyjzj中,整条支链在点Oj处的变形量可由构件i和构件j的变形量叠加而成。
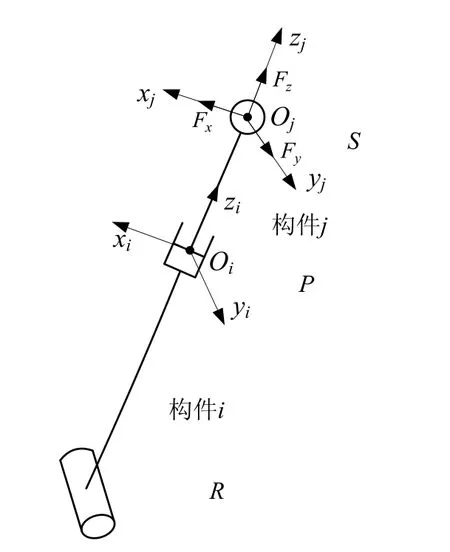
图2 单条支链受力变形
2.1 构件j的变形量
为了推导过程中表达的方便性,现对过程中出现的符号做出如下规定,为构件B对构件A在c点的作用力,为柔性构件A上c点处的变形量,为刚性构件B上c点处的位移量。
在坐标系Ojxjyjzj中,设动平台(构件k)在点Oj处对支链的作用力为因此把构件i刚化时,构件j在点Oj处的变形量可由结构力学中的单元柔度矩阵进行定量分析,即:

式(1)中,Cj为构件j的单元柔度矩阵,根据其局部坐标系的建立情况可得:

式(2)中,Lj为构件j的长度,mm;E和G分别为构件j的弹性模量和切变模量,GPa;Ix和Iy为构件j绕其局部坐标系Ojxjyjzj对应坐标轴的转动惯量,kg.mm2;IP为构件j对其局部坐标系坐标原点Oj的极惯性矩,kg.mm2。
2.2 构件i的变形量
在坐标系Oixiyizi中,将构件j视为刚体而构件i为柔性体时,构件i在点Oi处的变形量为:

式(3)中,Ci为构件i的单元柔度矩阵,其建立方法与式(2)同理。为求得力需要对构件j进行受力分析。
以构件j为研究对象,在节点Oi处建立如下力平衡方程:

由式(4)可得:
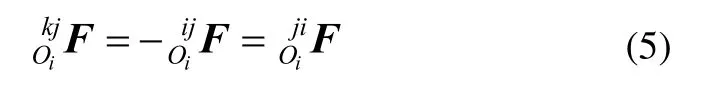
由式(3)和式(5)得:

根据理论力学中力的平移定理,将构件k在点Oj处对构件j的作用力平移到点Oi处为:


力平移时,在点Oi处所附加的力偶矩为:

由于点Oi是构件i和构件j的公共节点,由式(6)和式(7)可得:
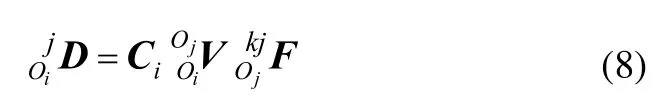
构件i的弹性变形引起了构件j的位移变化,但构件j在点Oi处和点Oj处的位移变化量是不同的,根据理论力学中刚体上任意两点的运动规律可得:

式(9)中,
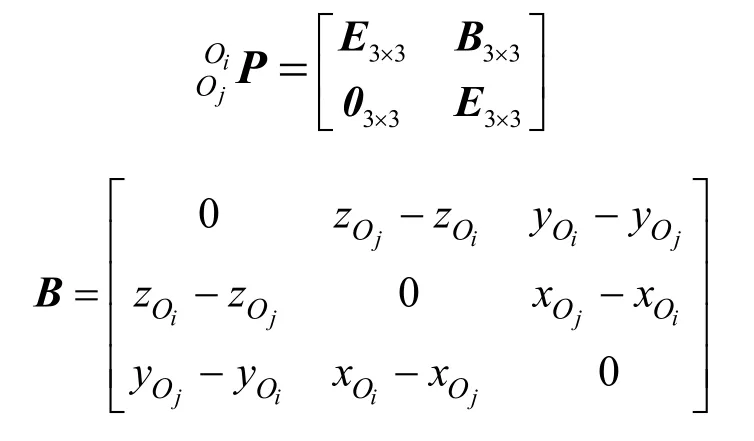
将式(8)代入式(9)中可得:

2.3 单条支链末端变形量
在坐标系Ojxjyjzj中,基于式(1)和式(10),根据小变形叠加原理可得单条支链的末端变形量为:

3 机构整体刚度矩阵
对于单条支链,在坐标系Ojxjyjzj中,由于点Oj是构件j和构件k(动平台)的公共节点,则:


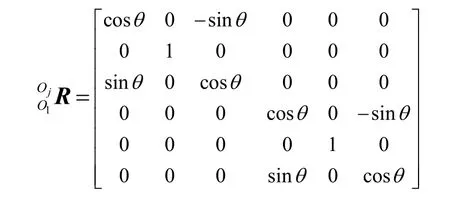
其中θ为轴O1x1和轴Ojxj的夹角,且在坐标变换过程中从轴O1y1正向看逆时针方向为正。
在定坐标系中,构件k的位移可以由刚体上任意一点的位移进行描述,且构件k在点Oj处和点O2处的位移量存在如下关系:
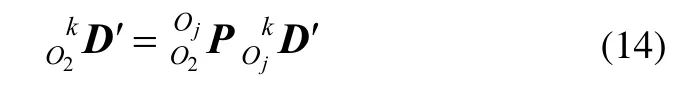
式(14)中,
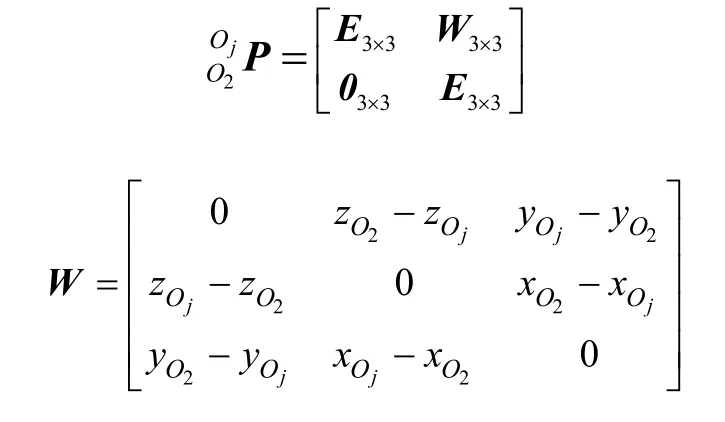
由式(11)~式(14)可得:
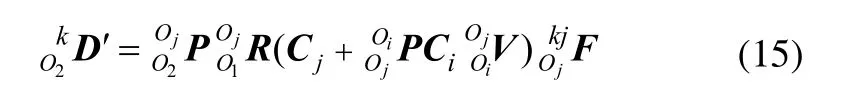
对于全部支链,根据式(15)可得:
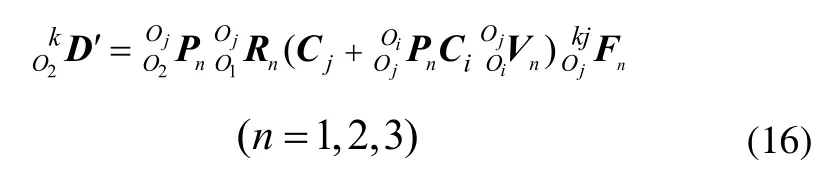
由式(16)可得构件k对各支链的作用力为:

根据理论力学中力的平移定理,将各支链在点Oj处对构件k的反作用力由点Oj平移到构件k的几何中心点O2处:
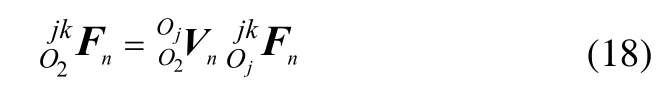
式(18)中:


力的平移过程中,在点O2处所附加的力偶矩为:

当机构静止时,动平台受力平衡,由式(17)、式(18)可在构件k的几何中心点O2处建立如下力平衡方程:

其中Ffz为动平台所受工作载荷:
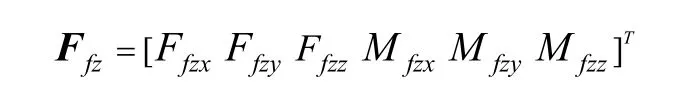
由式(19)可得:

其中K为机构的静刚度矩阵。

4 算例分析
机构参数如下:构件i和构件j的材料均选用45号钢,其弹性模量E=200GPa,切变模量G=80GPa。动平台边长为300mm,定平台底边长为900mm,各支链转动副到对应移动副的距离为360mm。构件i的横截面积为2500mm2,转动惯量Ixi=50154.85kg.mm2,Iyi=50157.46 kg.mm2。构件j的横截面积为900mm2,对应的转动惯量为Ixj=18476.39kg.mm2,Iyj=18476.39kg.mm2。设工作载荷为[100N,100N,100N,80N.m,80N.m,80N.m]T,任选动平台位姿[0mm,550mm,90°]T,则在定坐标系O1x1y1z1中,动平台的理论位姿变形量和基于ANSYS的测量值如表1、表2所示。

表1 线变形理论值和ANSYS测量值对比
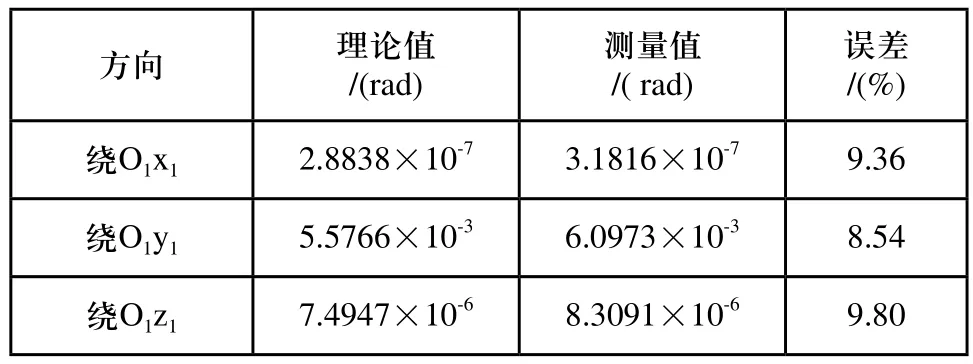
表2 角变形理论值和ANSYS测量值对比
由表1、表2可知,虽然机构只有三个自由度,但动平台在机构非自由度方向上也存在位姿变形。动平台参考点的线位移在沿轴O1y1的方向上最大,动平台的角位移在绕轴O1y1的方向上最大。动平台的位姿变形以线变形为主。
为分析机构静刚度在定姿态工作空间中的变化情况,令x的变化范围为-50mm~50mm,z的变化范围为500mm~600mm,θ=90°,该机构的静刚度特性曲面如图3~图8所示。

图3 机构沿轴O1x1线刚度

图4 机构沿轴O1y1线刚度
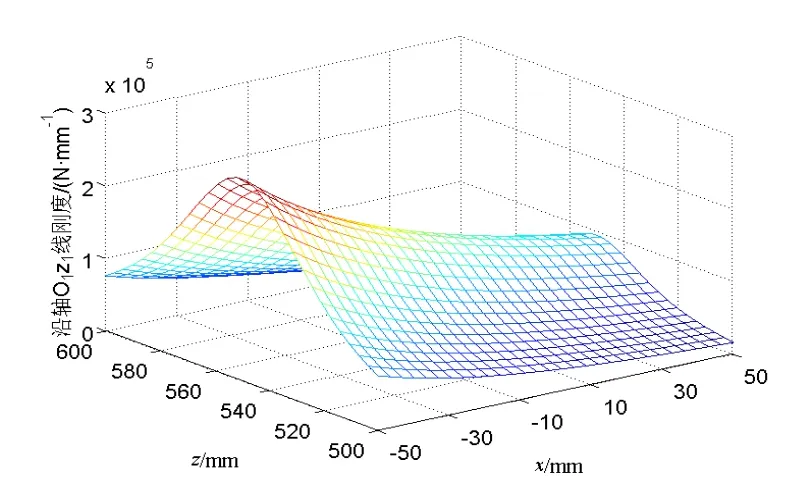
图5 机构沿轴O1z1线刚度

图6 机构绕轴O1x1角刚度

图7 机构绕轴O1y1角刚度

图8 机构绕轴O1z1角刚度
由图3~图8可知,机构静刚度随动平台参考点x值的改变而平稳变化,但是z值的改变使机构沿轴O1y1和O1z1的线刚度、绕轴O1x1和O1y1的角刚度存在波动。
5 结论
针对本文提出的新型3-RPS并联机构,从单元柔度矩阵角度出发,结合小变形叠加原理、刚体上任意两点的运动规律以及力的平移定理,建立了该机构的静刚度模型。根据数值算例中动平台的理论位姿变形量和ANSYS的有限元测量值验证了该建模过程的正确性。
基于静刚度模型绘制了机构在定姿态工作空间中的静刚度特性曲面,并给出了机构静刚度的变化规律。整个分析过程并未基于雅可比矩阵,能够定量描述动平台在机构自由度和非自由度方向的位姿变形量,对于其他少自由度并联机构的静刚度建模分析同样具有普遍适用性。
