基于反馈线性化的两轮自平衡汽车侧倾动态响应控制

熊宇聪，张 猛,2

（1.北京控制工程研究所，北京 100089；2.北京轩宇空间科技有限公司，北京 100089）

0 引言

随着智能交通工具研究的兴起，具有侧倾控制的两轮自平衡汽车凭借其外形轻巧、驾驶灵活等优点受到了国内外的广泛关注[1]。两轮汽车的动力学模型是典型的非线性欠驱动非完整约束系统[2]，在无相对滑动的理想情况下，两轮汽车的前后轮的横向和纵向运动均受到由地面形成的非完整约束，且两轮汽车在侧倾方向无直接驱动激励，因此在极低速行驶或静止的情况下，无法保持车身的平衡[3]。目前，针对两轮汽车模型欠驱动的特点，相关研究人员提出了多种控制机构以维持两轮汽车的自平衡，包括方向转向[4]，重量平衡体[5]和控制力矩陀螺仪（CMG）[6]三种控制机构。相较而言，控制力矩陀螺仪具有输出力矩大、易于使用电气控制等优点[6]，因此获得了广泛研究。通过控制力矩陀螺仪提供侧倾方向力矩，控制两轮汽车在侧倾方向获得期望的姿态响应是两轮自平衡汽车的关键技术之一。

文献[6]利用Euler-Lagrange方法推导了基于单个控制力矩陀螺仪两轮汽车的动力学模型，给出了一种基于模型的双环自抗扰控制方法（Active Disturbance Rejection Control），这种控制方法主要采用两个串联扩展状态观测器和两个具有自抗扰作用的状态反馈控制律，实现了两轮汽车的在侧倾角为2°范围内恢复平衡和对侧倾方向姿态干扰的抑制。文献[7]利用Euler-Lagrange方法推导了与文献[6]相似的两轮汽车动力学模型，并对得到的非线性模型在平衡点处进行了线性化，设计了状态反馈控制方法，使两轮自平衡汽车可从侧倾角为3°左右恢复平衡。文献[8]采用了与文献[6]相同的动力学模型，并设计了滑模变结构控制器，实验表明，该控制方法能使两轮汽车在侧倾角度为26°时恢复到直立平衡状态。文献[9]采用了文献[7]相似的两轮汽车动力学模型，在平衡点附近进行线性化，并提出了模糊滑模控制和自适应模糊滑模控制两种控制方法。实验表明，两种控制方法均能维持两轮汽车在平衡点附近的平衡状态，比较两种控制方法，自适应模糊滑模控制方法具有更强的抑制干扰能力。

对于两轮自平衡汽车侧倾方向的动力学模型为非线性动力学模型，上述文献均采用了平衡点处线性化处理方法，不可避免的存在线性化误差。此外，对于姿态控制，两轮自平衡汽车的动态响应和稳态响应是两个主要关注因素，而上述文献主要关注两轮自平衡汽车侧倾方向姿态控制的稳态响应，未开展动态响应过程分析。

本文综合研究了两轮自平衡汽车侧倾动态响应控制问题，采用反馈线性化方法将两轮自平衡汽车的非线性动力学模型转换为线性动力学模型，避免了两轮自平衡汽车动力学系统在平衡点附近的线性化处理，从而消除了线性化误差的影响。利用状态反馈对转换的线性动力学模型进行极点配置，设计两轮自平衡汽车侧倾方向的动态响应过程，建立两轮自平衡汽车侧倾方向动态响应指标与反馈系数之间的函数关系，在保证两轮自平衡汽车控制系统具有良好的稳态响应的同时，兼顾控制系统的动态响应。针对所设计的动态响应过程，采用PI控制器实现控制力矩陀螺仪的力矩输出调节，实现所设计的动态响应过程，满足相应的动态响应指标要求。最后，本文结合具体的仿真算例验证了所提出的基于反馈线性化控制方法的有效性。

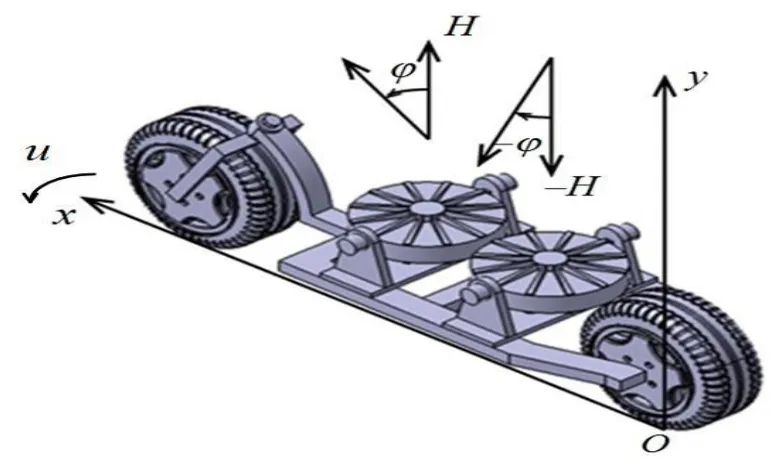
图1 两轮汽车底部机械结构图

图2 控制系统结构图

1 两轮自平衡车模型

1.1 系统结构

本节介绍两轮自平衡汽车机械结构和控制系统结构。图1给出了两轮自平衡汽车底部机械结构图。如图1所示，两轮自平衡汽车底部安装一组控制力矩陀螺仪对两轮汽车进行侧倾姿态控制，一组控制力矩陀螺仪反向旋转，在驱动电机作用下反向旋进，以产生侧倾方向的控制力矩。

图2给出了两轮自平衡汽车控制系统结构图。如图2所示，控制系统由测量单元、控制单元和执行单元三部分构成，三个部分通过车辆供电母线供电并通过车辆通信总线实现通信，控制单元包括自平衡控制器和CMG控制器，测量单元包括陀螺仪和加速度计，执行单元包括CMG和CMG驱动器。

1.2 动力学模型

图3给出了两轮自平衡汽车车体受力示意图。如图3(a)所示，两轮自平衡汽车保持直立状态时，O点与O'点分别为前后轮与地面之间的接触点，以后轮与地面接触点O为坐标原点，Ox轴与水平方向OO'轴重合，Oy轴沿铅垂方向，Oz轴根据右手法则确定，指：向纸面外。h为两轮自平衡汽车质心高度。如图3(b)所示，两轮自平衡汽车车体绕侧倾轴Ox轴发生侧倾运动时，侧倾角为地面对两轮汽车的弹力与摩擦力的作用线通过侧倾轴Ox，力矩为0，车体质量为m时，车体受到重力矩mghsin与控制力矩陀螺仪产生的控制力矩u的合力矩作用，矢量正方向为图示方向。由动力学原理，两轮自平衡汽车侧倾运动的动力学方程为：

其中，J为两轮自平衡汽车整车相对侧倾轴Ox轴的转动惯量。

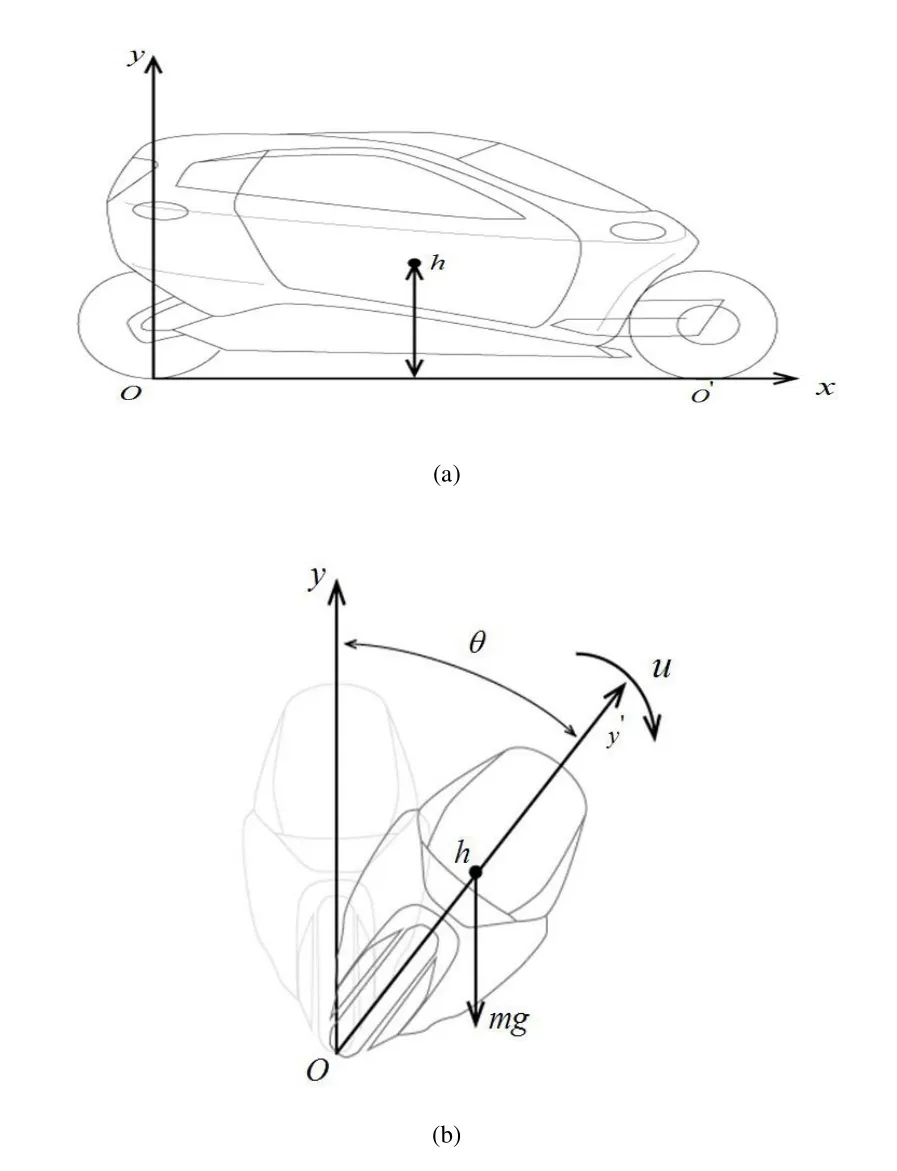
图3 两轮自平衡汽车受力图

两轮自平衡汽车自平衡系统由一组控制力矩陀螺仪和一组旋进电机组成，如图1所示。图4给出了控制力矩陀螺仪输出力矩图，当两轮汽车侧倾角度为时，控制力矩陀螺仪角动量所在的平面为Oxy'平面，两个控制力矩陀螺仪在驱动电机作用下反向旋进，旋进角的模为ϕ，旋进角速度的模为。单个控制力矩陀螺仪角动量H大小不变，旋进角度为ϕ时，其在侧倾轴Ox轴和Oy'上的投影分别为：

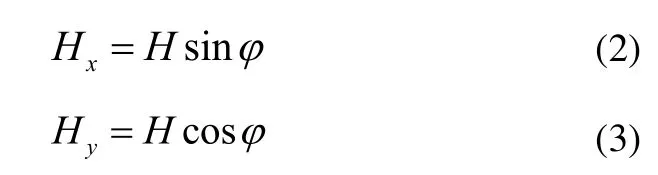
式(2)和式(3)求导得：

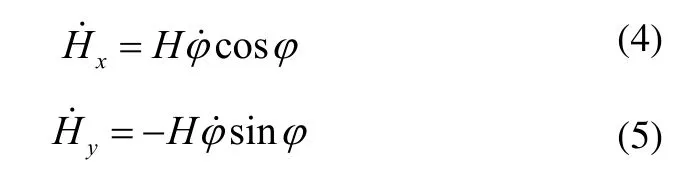
图4所示控制力矩陀螺仪之间具有对偶关系，因此控制力矩陀螺仪在旋进过程中角动量的总变化量为方向沿Ox正方向。根据角动量守恒，车体所受控制力矩u沿Ox轴负方向，大小为：

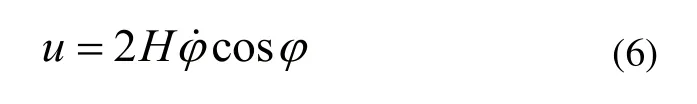
图4 控制力矩陀螺仪输出

2 控制系统设计

2.1 车体控制

根据式(1)，两轮自平衡汽车车体的动力学模型为非线性二阶系统。为了精确控制非线性二阶系统的动态响应，构造参考力矩输入uref，当控制力矩陀螺仪产生的实际输入u满足：

两轮自平衡汽车侧倾方向的动态响应满足期望动态响应指标要求。式(7)成立时，根据两轮自平衡汽车车体的动力学模型(1)，式(8)成立：

式(8)所对应的系统框图如图5(a)所示。

非线性二阶系统动态响应形式复杂，而在两轮自平衡汽车控制系统中，状态变量侧倾角度与侧倾角速度可以通过测量元件实时测量，在车体质量m，车体质心高度h已知的情况下，采用反馈线性化控制，在参考力矩uref中引入静态反馈作用量其控制系统框图如图5(b)所示，即：

其中，u1为参考力矩的线性作用部分。

式(9)代入式(8)得：

式(10)对应系统框图如图5(c)所示，通过在参考力矩uref中引入静态反馈作用量车体二阶非线性系统转换为二阶线性系统。利用状态变量侧倾角度与侧倾角速度可实现二阶线性系统动态响应的精确控制。设计状态反馈如图5(d)所示。

图5 车体控制设计

即：

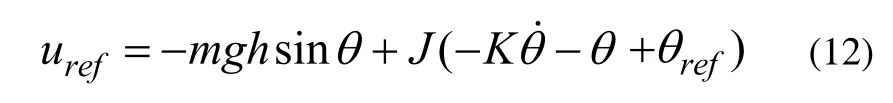
式(11)代入式(10)可得：

拉普拉斯变换得：

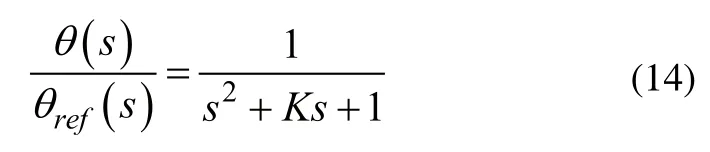
对于两轮自平衡汽车从初始侧倾角度恢复至直立状态，动态响应过程为阶跃响应[7]。

由于阶跃响应与单位阶跃响应相差常数倍，研究单位阶跃响应可以得到阶跃响应的全部性质，由式(14)，根据二阶线性系统理论当K=0时，两轮自平衡汽车的阶跃动态响应为无阻尼响应，响应过程为：

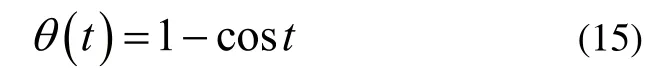
当0＜K＜2时，两轮自平衡汽车的阶跃动态响应为欠阻尼响应，响应过程的动态响应指标与速度反馈系数K之间的函数关系如下：

延迟时间td：

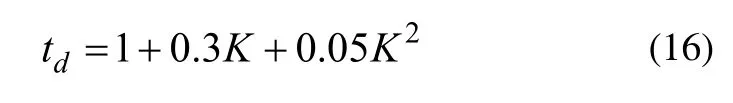
上升时间tr：

峰值时间tp：

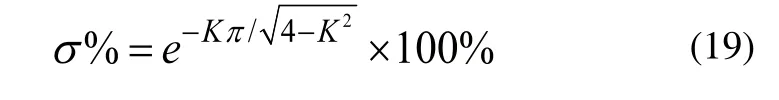
调节时间ts：

当K=2时，两轮自平衡汽车的阶跃动态响应为临界阻尼响应，响应过程为：

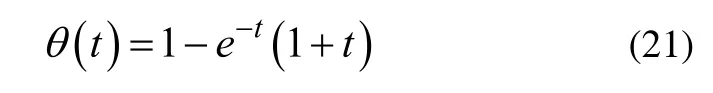
当K＞2时，两轮自平衡汽车的阶跃动态响应为过阻尼响应，响应过程的动态响应指标与K之间的函数关系为：

延迟时间td：

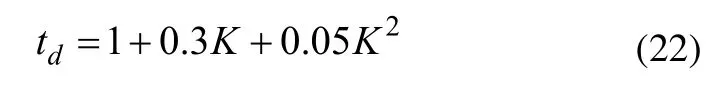
上升时间tr：

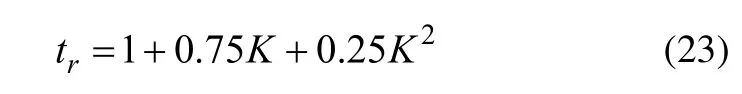
式(15)～式(23)建立了动态响应过程指标与速度反馈系数K之间的函数关系，通过调整K值可以使两轮自平衡汽车侧倾动态响应满足期望的动态响应指标。

2.2 控制力矩陀螺仪控制

为实现2.1节所设计的车体侧倾动态过程，控制力矩陀螺仪的输出力矩为：

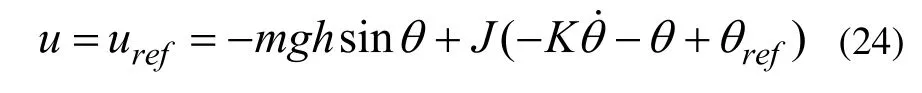
根据CMG的输出力矩模型(6)，参考力矩uref所对应的陀螺仪旋进角度ref与旋进角速度ref满足：

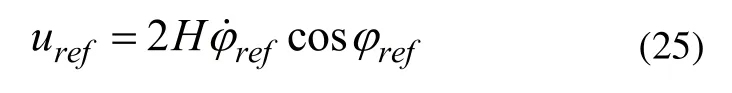
对比式(6)与式(25)，当控制力矩陀螺仪的旋进角度与旋进角速度满足式(26)时，式(24)成立。

控制力矩陀螺仪的旋进角速度由驱动电机控制，对于驱动电机，其调速控制式(26)可由单位负反馈结合PI控制器实现，如图6所示。

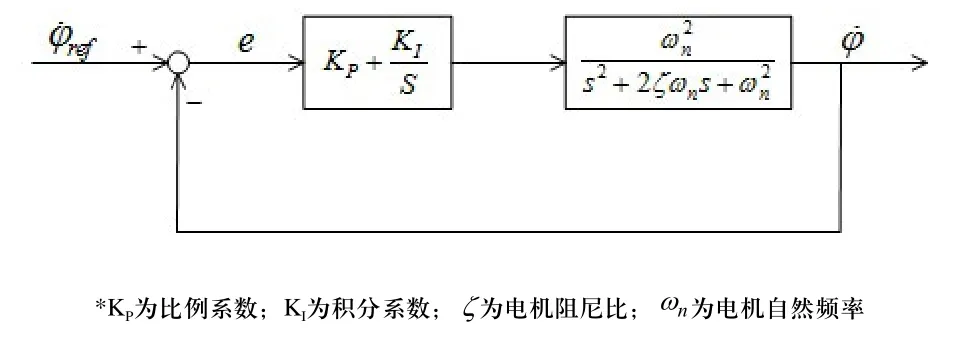
图6 驱动电机控制

2.3 稳定性证明

两轮自平衡汽车控制系统由两部分构成，分别为车体自平衡控制系统和控制力矩陀螺仪控制系统，控制系统工作原理如图7所示。由姿态测量单元测量两轮自平衡汽车当前侧

对于控制力矩陀螺仪控制系统，输入输出稳定的充要条件为图6所示闭环控制系统特征方程的根位于复平面的左半平面。

图6所示闭环控制系统的特征方程为：

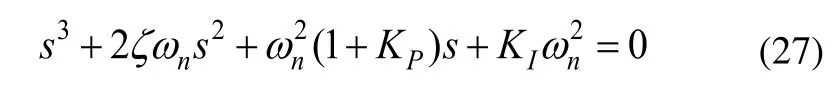
根据劳斯-赫尔维兹稳定性判据，式(27)的根位于复平面左半平面的充要条件是：

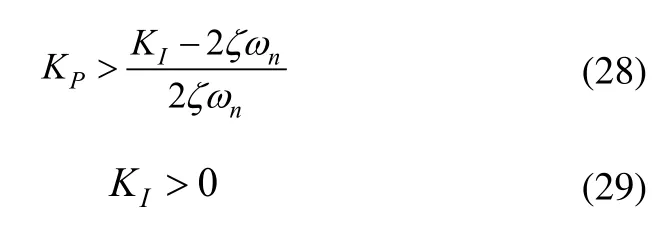
式(28)与式(29)成立时，控制力矩陀螺仪输入输出稳定。图6所示控制系统误差函数为：

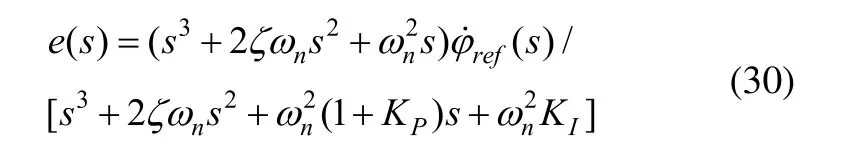
此时，式(26)和式(24)成立，从而两轮自平衡汽车侧倾方向动态响应为(14)，其特征方程为：

式(30)的根位于复平面左半平面的充要条件为：

当式(28)、式(29)、式(31)与式(33)同时成立时，控制系统输入输出稳定。

3 控制系统仿真

3.1 性能验证仿真参数

某车型两轮自平衡汽车相关物理参数如表1所示。

表1 两轮自平衡汽车相关参数

两轮自平衡汽车侧倾方向的姿态响应过程为阶跃响应。对于所设计的控制系统，两轮自平衡汽车能维持平衡的充要条件为式(24)成立。对于式(24)，具有如下性质：在任意非平衡位置处，控制力矩陀螺仪的输出力矩u的模大于车体所受重力矩mghsin的模，且两者方向保持相反。由表1参数计算可知，两轮自平衡汽车所受重力矩最大为490N.m。由于控制力矩陀螺仪随着驱动电机的旋进，输出力矩单调递减，为了满足两轮自平衡汽车保持平衡的充要条件，设置初始侧倾角度为15°，约0.26rad，控制力矩陀螺仪的最大输出为800N.m，参考侧倾角度为0°，即平衡位置。

图7 控制系统工作原理图

对于上述仿真条件，控制力矩陀螺仪控制器参数可选取KP=8，KI=2，自平衡控制器参数分别选取K=0（无阻尼），K=1（欠阻尼），K=2（临界阻尼），K=3（过阻尼）四种仿真参数分别验证式(15)～式(23)。

在MATLAB/SIMULINK软件中，选择Runge-Kutt积分方法，以1ms为定步长对本文提出的侧倾姿态控制方法进行性能仿真验证。

3.2 性能验证仿真结果

分别选取K=0（无阻尼），K=1（欠阻尼），K=2（临界阻尼），K=3（过阻尼）四种仿真参数对两轮自平衡汽车侧倾方向动态响应进行验证，仿真结果如图8所示。

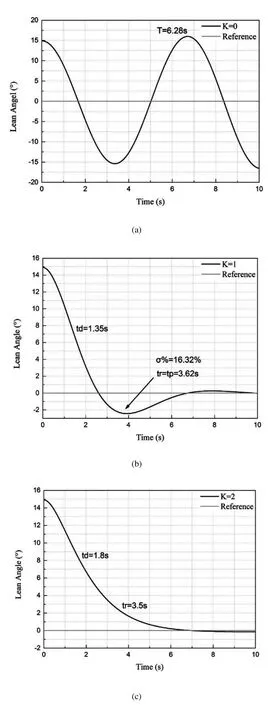
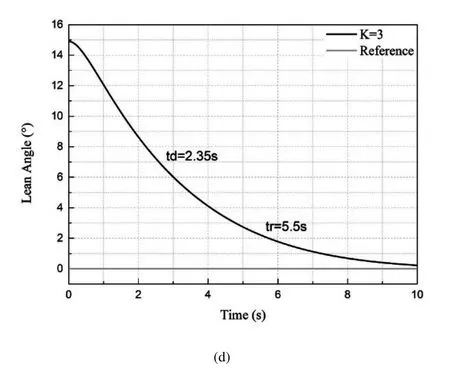
图8 性能验证结果

从图8(a)可以看出，当K=0时，两轮自平衡汽车在控制器作用下在平衡位置附近做等幅振荡运动，振幅为15°，振荡周期为T=6.28s，符合式(15)计算得到的动态响应。在图8(b)中，两轮自平衡汽车车体侧倾动态响应为欠阻尼响应，根据(16)式～式(20)计算，延迟时间td=1.35s，最大峰值时间tp与上升时间tr为3.62s，超调量为σ%=16.32%，与仿真实验结果一致。从图8(c)与图8(d)可以得出，当K=2和K=3＞2时，两轮自平衡汽车侧倾方向动态响应为临界阻尼响应和过阻尼响应，根据式(21)～式(23)式计算，延迟时间td分别为1.8s和2.35s，上升时间分别为3.5s和5.5s，与实验结果一致。由上述实验结果可知，通过改变自平衡控制器的速度反馈系数K值，可以定量调整两轮自平衡汽车车体侧倾方向响应的动态指标，动态响应指标与K值之间的函数关系式为式(15)～式(21)。

3.3 动态响应设计与仿真

为说明本文提出的控制器对两轮自平衡汽车侧倾动态响应的控制能力，针对侧倾动态响应的动态响应指标约束，计算符合约束要求的速度反馈系数K值，进一步仿真验证。

在初始侧倾角度为30°时，回复至平衡状态的动态响应指标要求如下：

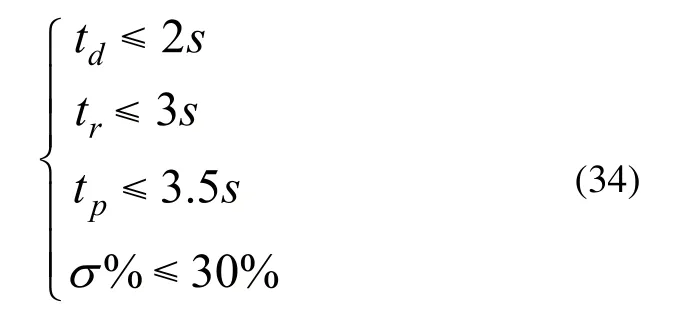
解上述不等式组(35)，可得速度反馈系数满足0.714≤K≤0.88，选取K=0.8，进行仿真验证，结果如图9所示。将K=0.8代入式(16)～式(20)计算可得td=1.272s，tr=2.16s，tp=3.426s，σ%=25%满足动态响应指标约束。

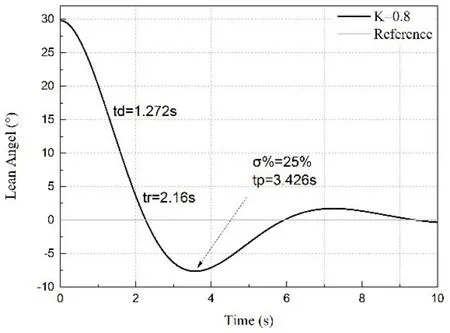
图9 动态响应设计结果

4 结论

对于有驾驶人员参与驾驶的两轮自平衡汽车，车体侧倾方向姿态控制系统的动态响应和稳态响应是两轮自平衡汽车侧倾姿态控制的两个重要因素。本文提出了基于反馈线性化的控制综合控制方法，利用反馈线性化将两轮自平衡汽车的非线性动力学模型转换成为线性动力学模型，消除了在平衡点处线性化引起的线性化误差。针对线性动力学模型设计了状态反馈，并建立速度反馈系数K与动态响应指标之间的函数关系，通过改变速度反馈系数K，可准确改变两轮自平衡汽车侧倾方向动态响应指标，定量设计动态响应过程。针对所设计的动态响应过程，本文为提供侧倾力矩的控制力矩陀螺仪输出力矩调节设计了PI控制器，并证明了整车控制系统的输入输出稳定性，为两轮自平衡汽车侧倾方向姿态控制提供了一种新的控制算法。最后通过具体车型的仿真结果说明了本文提出的控制算法的有效性。