六自由度工业机器人3D仿真系统研究

吴传奇，甘 屹，齐从谦

（1.上海理工大学 机械工程学院，上海 200093；2.同济大学 机械与能源工程学院，上海 201804）

0 引言

六自由度工业机器人适用面广，主要运用于码垛、焊接等工业领域。对其进行运动学建模与仿真，可以降低机器人生产成本与提高执行效率[1]。现阶段多数大型机器人厂商的仿真系统较好的实现了可视化与运动学仿真如ROBCAD[2]，但是封闭程度较高。另一部分则采用MATLAB[3]、ADAMS[4]以及二者结合等方式[5]，适合教学与研究，但其可移植程度较低。其他则采用高级语言如VRML、OpenGL[6]等，但其建模较为困难且3D可视化运动效果较差。

针对现阶段工业机器人仿真系统封闭程度高且3D可视化运动效果较差的缺点，本文以六自由度工业机器人为研究对象，开发了一种运用Microsoft Visual C#2015的WPF设计的3D仿真及控制系统软件。通过该软件对机器人正、逆运动学算法及综合优选算法进行了现场验证并同步了机器人数字模型3D实时仿真与机器人物理本体的实时同步。具有较好的系统可移植性与3D可视化运动效果。

1 运动学分析

1.1 连杆坐标系的建立

本文采用D-H法进行求解。在机器人关节1的轴线上建立基坐标系x0y0z0并依次建立机器人各个连杆的坐标系。x6y6z6为机器人末端坐标系。机器人各关节的D-H坐标系如图1所示。

图1 机器人D-H坐标系

1.2 正运动学求解

机器人DH参数如表1所示。

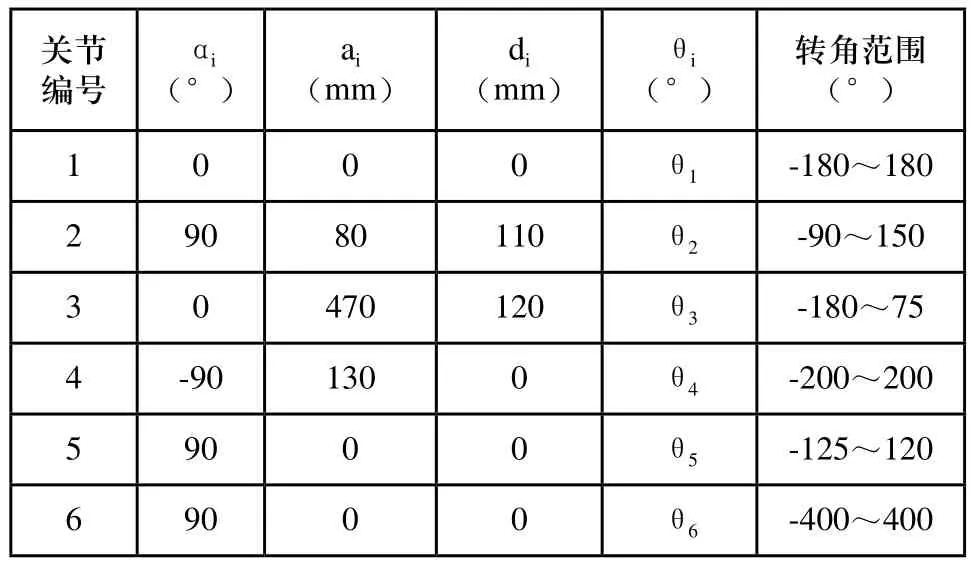
表1 机器人D-H参数表

机器人相邻杆件间的坐标转换矩阵如式(1)所示。

将各连杆间坐标转换矩阵相乘得机器人末端坐标系到基坐标系的转换矩阵，如式(2)所示。

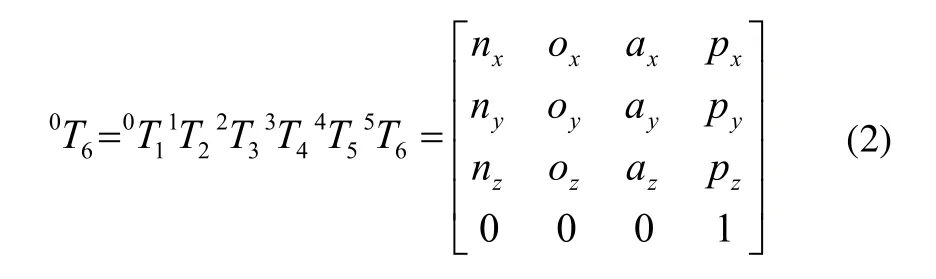
(n,o,a)为姿态矩阵。实际应用中，为了与机器人的末端的位姿表示一致且提高运行速度，工业机器人大多采用一组广义的坐标来表示位置和姿态。其中（px，py，pz）表示机器人的位置矩阵，欧拉角表示姿态。

1.3 逆运动学求解

在已知D-H参数和机器人末端位姿的基础上，对式(2)分别相乘所对应的逆矩阵，从而求得各关节的转角。例如对θ1的求解，式(2)两端同时乘逆矩阵0T1-1后得：

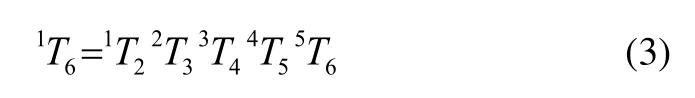
左右两端对应元素相等得：

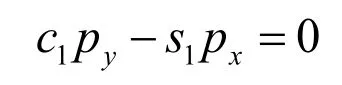
解得θ1：

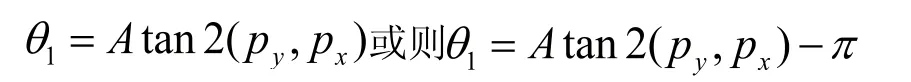
同理可得：

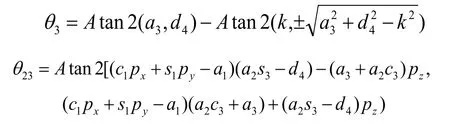
当s5≠0时：

由D-H参数知各关节运动范围是有限制的，因此需对多组解进行筛选。对多组解的筛选通常有能量最小原则、行程最短原则[7]等。根据行程最短原则，其优选函数如式(5)所示。

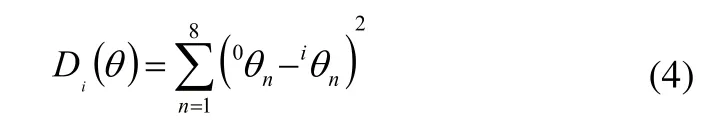
根据能量最小原则，其优选函数如式(6)所示。

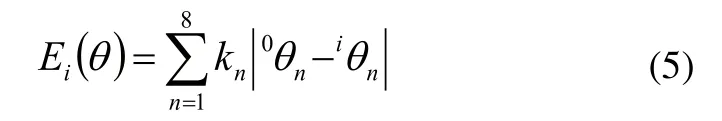
本文综合考虑能量最小原则以及行程最短原则。得出综合优选函数如式(7)所示。

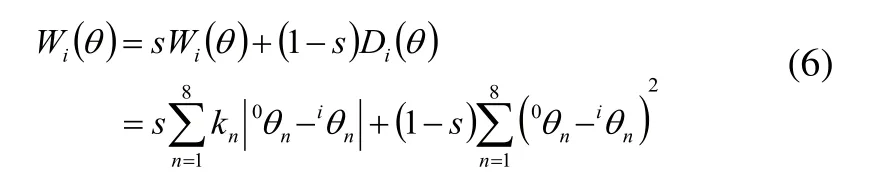
式中s为权重系数。

2 3D仿真及控制系统设计

运用Microsoft Visual C#2015的WPF设计了3D仿真及控制系统软件，此系统基于WPF多媒体交互用户图形系统，采用其内置3D渲染建模引擎构建矢量旋转矩阵，并以C#编程语言设计运动控制逻辑。在系统示教模式下可实现机器人初始化、正运动学计算、工程的存取、时间及速度显示；在系统滚轮模式下可实现逆运动学的计算；运行状态的显示、各关节运动。

机器人3D仿真及控制系统界面如图2所示。

图2 3D仿真及控制系统软件界面

3 机器人实时控制实验

在示教模式下，输入各关节角度值（40，-135，30，0，-90，0），通过3D仿真及控制系统可计算出机器人末端位姿运动学正解并同时传给机器人实物本体，在系统界面实时显示数字3D位姿，正运动学求解位姿图如图3所示。

图3 正运动学求解位姿图

在滚轮模式下，3D仿真及控制系统实时采集到机器人实物本体的关节末端位姿（16.22，0.00，921.27，-173.32，-15.00，-6.68），通过3D仿真及控制系统可计算出机器人末端位姿运动学逆解并传给机器人数字3D模型，在系统界面实时显示数字3D位姿，逆运动学求解位姿图如图4所示。

图4 逆运动学求解位姿图

4 结束语

本文对六自由度工业机器人运动学进行了研究。采用D-H法建立了机器人连杆坐标系，由正运动学算法得出了以末端位置矢量和欧拉角表示的末端位姿；采用代数解析法对机器人逆运动学进行求解并用综合优选算法对多组解进行了最优解的筛选。运用Microsoft Visual C#2015的WPF设计了3D仿真及控制系统软件。通过生产现场验证，表明本文所采用的正、逆运动学算法以及综合优选算法有效并且实现了3D仿真及控制系统中的机器人实时数字3D运动位姿和机器人本体实际末端位姿保持一致，具有优良的机器人运动可视化效果和系统可移植性能。