“将错就错” 物尽其用
——对一道课本习题的变式探究
2018-07-21安徽
安徽
陈晓明
(作者单位:安徽省宣城市宁国市宁国中学)
“将错就错” 物尽其用
——对一道课本习题的变式探究
安徽
陈晓明
在一堂习题课上,笔者在对一道习题进行变式时,一不小心将题目中一个条件写错,改变了笔者课前的预设,笔者没有慌乱,没有及时更正,而是“将错就错”,让学生继续探究,没想到却有了新的发现,得到更完美的结论,真是物尽其用.
题目(人教A版普通高中课程标准实验教科书《数学必修2》第90页习题3.1B组第6题)经过点P(0,-1)作直线l,若直线l与连接A(1,-2),B(2,1)的线段总有公共点,找出直线l的倾斜角α与斜率k的取值范围,并说明理由.


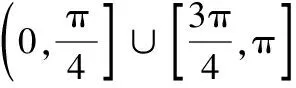

点评:这种解法很巧妙.从另外一个完全不同的视角来求斜率范围.采取待定系数法,先设出直线方程,然后利用二元一次不等式与表示的平面区域的关系得到关于k的不等式,从而求出k的范围.本解法充分利用了“A(1,-2)与B(2,1)总在直线MP的两侧”与“直线l与连接A(1,-2),B(2,1)的线段总有公共点”之间的等价关系.学生很难想到这种方法,需要教师引导.同时,作为教师也要强调这种用不同表现形式表达同一个事物在数学中的重要性.
在讲完这道课本题后,笔者在课前准备对这道题进行下面的变式.
变式1(预设):将原题中A(1,-2)改为A(-3,2),其余条件不变,求解问题不变.
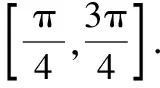


可是,在课堂上发生了意外:笔者在对原课本题进行变式时一不小心错将B点坐标改成了B(-3,2),笔者当时没有看出来,发现时本想再改过来,可学生已经在思考了,回头一想,将错就错,就让学生做一做,看看情况怎样.
变式2(生成):将B点坐标改为B(-3,2),而其他条件不变,求解问题不变.
点评:学生经过计算直线AP,BP的斜率,发现kAP=kBP=1,于是A,B,P三点共线,如图所示.经过点P(0,-1)作任意一条直线l,都与连接A(1,-2),B(-3,2)的线段总有公共点,因此直线l的倾斜角α的取值范围是[0,π),除了直线l处于竖直位置时斜率不存在外,其余位置斜率k的取值范围为R.





完成这个变式探究,学生们很是感慨,“数学使人周密”真是不假啊!
这时,笔者又接着补上了变式1.大家就觉得变式1很简单了.
不知不觉课堂气氛在探究中变得活跃起来,在教师的启发下,有同学提出了一些新问题,也有同学反思总结出一些结论,甚至让笔者也感到惊喜,受益匪浅,真是教学相长啊!

教师:对呀,同学们在课后可继续探究,看看有什么异同,找找规律.
学生2(反思总结1):直线l从一个位置转到另一个位置的过程中,若只经过水平位置,则直线l的斜率k的取值范围为一个整体区间,倾斜角α的取值范围为两部分的并集.若只经过竖直位置,则直线的斜率取值范围是两部分的并集(其中当直线处于竖直位置时斜率不存在),而直线l的倾斜角α的取值范围为一个整体区间.若既经过水平位置,又经过竖直位置,则斜率与倾斜角的取值范围都为两部分的并集.
教师:你总结得很好.
马上有同学问道“若既不经过水平位置,又不经过竖直位置,则斜率与倾斜角取值范围呢”?也很快有学生答上“都为一个整体区间”.
教师:不错,各种情况都有了.
就在这时,班上有名的数学王子举手了,“我有记住结论的好方法”.
教师:那你快说说看.

教师:太精辟了,多好的“取两边”,“取中间”,很好记住,能让我们快速解题.在哪里我们还讲过“取两边”,“取中间”啊?
学生很快想到了一元二次不等式的解集,知识之间的联系真是奇妙啊!
教学感悟

(作者单位:安徽省宣城市宁国市宁国中学)
